
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод нелінійного програмування
|
|
|
|
Якщо цільова виробнича функція g (x1,x2,…xn) або нерівності (рівності) f(x1,x2,…xn) ≤ 0 (i=1,2,…m) обмежуючих умов, є криволінійні (нелінійні) функції від n змінних (факторів)х1, х2, …хn., то маємо задачу нелінійного програмування. Прикладом нелінійного програмування може бути квадратичне програмування, для якого цільова функція є квадратична функція, а обмежуючі нерівності (рівності) є лінійні функції. Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише певне наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.
В основі градієнтних методів лежить основна властивість градієнта диференційовної функції - визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.
Розглянемо метод Франка - Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.
Нехай необхідно відшукати
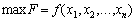
за лінійних обмежень:
 ;
;
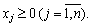
Допустимо, що Х 0 - початкова точка, що належить множині допустимих планів даної задачі. В деякому околі цієї точки нелінійну цільову функцію замінюють лінійною і потім розв’язують задачу лінійного програмування. Нехай розв’язок лінійної задачі дав значення цільової функції F 0, тоді з точки Х 0 в напрямку F 0 необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х 1, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.
Розглянемо детальніше перехід віди k -ої ітерації методу до (k + 1)-ої ітерації.
Припустимо, що відома точка Xk, яка належить області допустимих розв’язків. У даній точці обчислюємо градієнт цільової функції:
 .
.
Значення градієнта функції задає в даній точці напрям найшвидшого її зростання.
Замінюємо цільову функцію задачі лінійною функцією виду:
 .
.
Потім розв’язуємо задачу лінійного програмування з обмеженнями початкової задачі і новою цільовою функцією:

за умов:
 ;
;
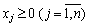 .
.
Нехай розв’язком такої задачі є точка 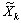 .
.
З початкової точки  в напрямку
в напрямку 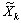 рухаємося з деяким довільним кроком
рухаємося з деяким довільним кроком  , визначаючи координати нової точки
, визначаючи координати нової точки  у такий спосіб:
у такий спосіб:
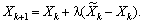
Зауважимо, що значення параметра  доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі
доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі  .
.
Для точки Хk +1 повторюємо розглянутий процес, для чого знову розраховуємо значення градієнта і т. д.
У такий спосіб знаходимо послідовність точок  , які поступово наближаються до оптимального плану початкової задачі. Ітераційний процес повторюється до того моменту, поки значення градієнта цільової функції не стане рівним нулю або виконуватиметься умова
, які поступово наближаються до оптимального плану початкової задачі. Ітераційний процес повторюється до того моменту, поки значення градієнта цільової функції не стане рівним нулю або виконуватиметься умова  , де
, де  - досить мале число, яке означає потрібну точність обчислень.
- досить мале число, яке означає потрібну точність обчислень.
Приклад. Підприємство виробляє два види продукції (А і В) і використовує на виробництво три види ресурсів: І, ІІ, ІІІ. Витрати ресурсів на виробництво одиниці кожного виду продукції подано в табл. 2.8.
Таблиця 2.8
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 905; Нарушение авторских прав?; Мы поможем в написании вашей работы!