
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математична постановка (формалізація) задач лінійного програмування
|
|
|
|
Лінійним програмуванням (ЛП) називається розділ математичного програмування, якою займається вивченням лінійних моделей.
Лінійне програмування має справу з оптимізацією моделей, в яких цільова функція лінійно залежить від змінних рішення і обмеження є лінійними рівняннями або нерівностями відносно переменных решения. Фактично це означає, що цільова функція і обмеження можуть бути тільки сумами произведений постійних коефіцієнтів на змінні рішення в першому ступені, тобто вирази типу (2.41):
C1X1 + C2X2 + CnXn. (2.41)
Головним етапом побудови математичної моделі вирішуваної задачі є формулювання завдання: ідентифікація змінних, обмеження на змінні, які диктуються умовами завдання. Обмеження зададуть безліч допустимих значень змінних. Важливий момент - визначення мети. Для її досягнення треба вибрати ті, що відповідають найкращому рішенню змінні. Формулювання мети на математичній мові приведе до побудови цільової функції. Методи знаходження оптимального плану залежать від конкретного виду цільової функції і безлічі допустимих значень, на якій вона задана.
Основні поняття лінійного програмування розглянемо на прикладі.
Підприємство виробляє три види продукції (П1, П2, П3), витрачаючи два ресурси (Р1 і Р2). Витрати (а) на виробництво одиниці продукції відомі: ресурсу Р1 = 12 (а1 = 2; а2 = 3; а3 = 7); ресурсу Р2 = (в1 = 2; в2 = 10; в3 = 2).
Сумарна кількість продукції П1 і П2 має дорівнювати 4, кількість продукції П3 не менше 2. Собівартість одиниць продукції рівна: П1 = 2 тис. грн, П2 = 3 тис. грн, П3 = 4 тис. грн Неохідно скласти план виробництва, при якому собівартість мінімальна.
Рішення. Позначимо планову кількість продукції П1: хj (j = 1, 2, 3) та собівартість продукції L = 2x1 + 3x2 + 4x3.
Витрати ресурсу Р1 дорівнюють 2х1 + 3х2 + х3; витрати ресурсу, Р2: 2х1 + х2 + 2х3 і повинні задовольняти умовам: ресурсу Р1 <=12, ресурсу Р2 <= 14. За умовами завдання x1 + x2 = 4, x2 >= 2.
Математична модель завдання така. Знайти значення невідомих х1, х2, х3, определяющие мінимум функції:
L= 2x1 + 3x2 + 4x3 (2.42)
і задовольняючії умовам:
2х1 + 3х2 + х3<=12
2x1 + x2 + 2x3<= 14
x1 + x2 = 4 (2.43)
x2>= 2
х1>= 0, x2>= 0, x3>= 0.
Така задача називається загальним завданням лінійного програмування.
Символічний запис такого завдання: знайти значення змінних х1, х2, х3, при яких функція:
L = с1x1 + с2x2 + с3x3 +....+ сnxn (2.44)
задовольняє умовам (2.45):
A11X1 + A12 X2 +.. + A1nXn = B1
A21X1 + A22X2 +... + A2nXn= B2
- - - - - - - - - - - - - - - - - - - - - - - - - - - (2.45)
Am1X1 + Am2X2 +... + AmnXn = Bm
х1>= 0, xn >= 0, деякі з чисел1,2,3……..,n.(2.46)
Систему обмежень можливо скласти у матричної формі:
А = Х ≤ В
де А =  ; Х =
; Х = 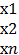 В =
В =  (2.47)
(2.47)
Потрібно знайти таке позитивне рішення системи (2.45), тобто Х1>0, Х2>0,..., Хn>0, при якому лінійна форма перетворювалася б в мінімум (максимум). Таку форму запису задачі називають канонічною и ей присущи слідуючі особливості:
1. Максимізувати цільову функцію (2.44);
2. Усі вільні члени умов задачі ненегативні;
3. Усі обмеження задачі мають вигляд рівності;
4. Серед векторів стовпців матриці є єдиний базис;
5. Умови позитивності зміних накладені на усі змінні.
Скорочено у математичному вигляді основну задачу лінійного програмування (ЛП) можливо записати, як:
знайти:
Z =  →extr
→extr 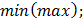 (2.48)
(2.48)
за наступних обмежень:
 для i = 1,2,…m; j = 1,2,…n; (2.49)
для i = 1,2,…m; j = 1,2,…n; (2.49)
та невід’ємності змінних:
Xj ≥ 0. (2.50).
Систему (2.44) називають системою обмежень, а лінійну форму (2.45) - цільовою функцією даної задачі. Умова невід’ємності (позитивності) в лінійного програмування вводиться тому, що будь-який план використання ресурсів не має на меті включати які-небудь ресурси галузі у від’ємній кількості. Наприклад, поголів’я худоби в якому - небудь господарстві або є, тобто його кількість більше нуля, або немає зовсім, тобто дорівнює нулю.
Від’ємне значення поголів’я худоби не мало б економічного змісту. Тому всі невідомі, що входять в задачу, повинні бути невід’ємними.
Існує нескінченна множина рішень системи (2.44).
Будь - яке невід’ємне рішення системи називають допустимим, а допустиме рішення, що перетворює лінійну форму в максимум (або мінімум), називають оптимальним рішенням.
Частіше всього в задачах не обов’язково повинні бути використані всі ресурси. В цих випадках система обмежень (2.45) буде задана у вигляді нерівностей виду (2.509.) або (2.51).
A11X1 + A12X2 +... + A1n Xn ≤ B1
A21 X1 + A22X2 +... + A2nXn ≤ B2
- - - - - - - - - - - - - - - - - - - - - - - - - (2.50)
Am1X1 + Am2X2 +... + AmnXn ≤ Bm
A11X1 + A12X2 +.. + A1n Xn≤ B1
A21X1 + A22X2 +... + A2nXn ≥ B2
- - - - - - - - - - - - - - - - - - - - - - - - - - - (2.51)
Am1X1 + Am2X2 +.. + AmnXn ≥ Bm
Подібні системи намагаються привести до канонічного вигляду, тобто до вигляду (2.45). Для цього до лівої частини нерівностей додаються в системі (2.50) деякі додатні невідомі, а в системі (2.51) - від’ємні. Обмеження можуть бути задані також у вигляді змішаної системи нерівностей, які містять нерівності і виду (2.50) і виду (2.51.
Планом або допустимим рішенням задачі ОЛП називається будь - який набір числових значень змінних, що задовольняє умовам (2.50) і (2.51). План можна записати у вигляді вектору Х → (x1,……… хn).
Оптимальним планом або оптимальним рішенням задачі ОЛП називається такий її план, при якому цільова функція має max або min. Значення цільової функції на оптимальному плані називається оптимальним значенням.
Базисним планом завдання КЛП називають план, в якому значення усіх вільних змінних є, - нулі, а значення базисних змінних - ненегативні. Базисний план називають - невироджений, якщо базисні змінні позитивні; Базисний план називають - вироджений, якщо серед базисних змінних - нулі.
Рішення задач лінійного програмування ведеться за певними правилами, що називаються алгоритмами рішень. Алгоритми діляться на дві групи.
До першої групи відносяться універсальні алгоритми, за допомогою яких можуть бути вирішені всі лінійного програмування. Найбільш розповсюдженим із них є симплекс - метод. Симплекс - методів є два: прямий симплекс - метод застосовується щодо рішення моделей типу (2.50), симплекс - метод зі штучним базисом застосовується щодо рішення моделей типу (2.51).
При розробці математичної моделі для вирішення задач за допомогою цього методу необхідно, щоб система нерівностей не була суперечливою інакше задача не буде мати вирішення. В повинні бути представлені лише найбільш важливі змінні і умови. Важливо визначити, чим відрізняються основні змінні від додаткових допоміжних. При запису умов математичній формі необхідно суворо стежити за знаками нерівностей.
До другої групи відносяться спеціальні методи, що застосовуються при вирішенні тільки окремих класів задач лінійного програмування, наприклад, метод потенціалів для задач по перевезенню вантажів, а також розподільчих задач.
Використання симплекс - методу (СМ) при знаходженні оптимальних рішень задач ЛП вручну, при загальній кількості змінних більше 10 долготривалі, трудомісткі з вірогідною часткою помилок. Тому виникає реальна необхідність при рішенні задач ЛП застосування сучасної обчислювальної техники (ПЕОМ).
Уданий час програмна реалізація СМ широко представлена в готових пакетах прикладних програм, які успішно використовуються для рішення задач ЛП з використанням ПЕОМ.
У математичному моделюванні існує три форми запису моделі: структурна (математична), розгорнута (числова) і матрична (таблична).
Під структурною математичною моделю розуміють компактную формализовану запись усіх умов задачі за допомогою символів індексов і інших зазначень. Структурна модель задачі складаеться з трьох частин: цільова функція, лінійни обмеження та умови неотрицательності змінних.
Розгорнута (числова) модель тобто запевнення конкретним числовим змістом.
Третья форма записи экономико - математичної моделі − матриця. Матриця це прямокутня таблиця, у якої в відповідності со структурною і разгорнутої формами запису моделі містится уся необхідна інформация для рішення даної задачі. Отличие матрици від структурної и развернутой моделі заключается в том, що в матриці конкретно и повністю надано значення кажної переменной, кажного обмеження, показывается їх сенс.
Схема матрици економико-математичної моделі наведена ніжче (табл. 2.6):
Таблиця 2.6
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1517; Нарушение авторских прав?; Мы поможем в написании вашей работы!