
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Залежність продуктивності корів від кількості згодовуваних кормів
|
|
|
|
| Угруповання господарств по продуктивності корів, ц. | Середнє значення продуктивності | Число господарств | Кількість згодованих кормів, ц корм. од. |
| 21 - 23,7 | 22,35 | 29,8 | |
| 23,7 - 26,4 | 25,05 | 31,3 | |
| 26,4 - 29,1 | 27,75 | 34.6 | |
| 29,1 - 31,8 | 30,45 | 35,7 | |
| 31,8 - 34,3 | 33,05 | 40,8 | |
| Σ | - | - |
Форма зв'язку (2.27):
у = а + вх, (2.27)
де у - річний удій молока на корову, ц.;
х - рівень витрати кормів на корову в рік, ц. корм. од.;
а і в - параметри рівняння;
а - початок відліку, або значення у при х = 0;
в - коефіцієнт пропорційності, що характеризує міру залежності у від х.
Коефіцієнт пропорційності називають ще коефіцієнтом регресії, а рівняння зв'язку - рівняння регресії. Рішення рівняння зв'язку зводиться до визначення невідомих параметрів рівняння - а і в. Необхідно знайти таке значення а і в, яке б найбільш повно характеризувало зв'язок між ознаками в середньому. Досягти цього можна тільки в тому випадку, якщо сума квадратів відхилень фактичних значень у від обчислених за рівнянням  х буде матиме найменше значення. Цю умову можна записати наступним чином (2.28):
х буде матиме найменше значення. Цю умову можна записати наступним чином (2.28):
Σ(у −  х)2 = min (2.28).
х)2 = min (2.28).
Прийом перебудови  х, при якому, Σ(у −
х, при якому, Σ(у −  х)2 називається методом найменших квадратів.
х)2 називається методом найменших квадратів.
Для виконання поставленої умови слід вирішити систему рівнянь.. Нормальні рівняння будують таким чином: вихідне рівняння перемножують спочатку на коефіцієнт при першому невідомому (а) і отримані вирази підсумовують. Потім вихідне рівняння перемножують на коефіцієнт при другому невідомому (в), отримані результати також підсумовують.
У розглянутому рівнянні у = а + вх коефіцієнт при другому невідомому дорівнює 1; отже, рівняння після перемноження зберігає вигляд:
у = а + вх,
а після підсумовування:
na + в Σ х = Σу.
Коефіцієнт при другому невідомому - х; множуючи на нього усі члени рівняння, отримаємо (2.29):
ах + вх2 = ху, (2.29)
а після підсумовування (2.30)
Σ ха + Σ х2 в = Σ ху (2.30)
Значення Σ у, Σх, Σху, Σу2 розраховуємо за даними спостереження.
Із таблиці 2.3 вибираємо Σ у, Σх, Σху, Σу2 і Σху і записуємо систему рівнянь:
22а + 773,5в = 636 22
773,5а + 27533,95в = 22627,12 773,5 ділимо
а + 35,1591 в = 28,909
а + 35,5966 в = 29,2529
і отримаємо 0,4375 в = 0,3439
вираховуємо перше з другого:
в = 0,786
а = 28,909 – 35,1591 × 0,789
а = 28,909 – 27,635 = 1,274
Звідси рівняння зв'язку (2.31):
у = 1,274 + 0,786х. (2.31)
Підставляючи дані х з таблиці 2.3, отримуємо розрахункове значення  х и (у −
х и (у −  х)2:
х)2:
Для розрахунку коефіцієнта кореляції використовуємо:
r =  σ2 ост =
σ2 ост =  ; σ2 ост =
; σ2 ост = 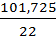 = 4,624
= 4,624
σ2 ост=  – (
– ( )2; σ2 ост =
)2; σ2 ост =  – 28,9092 = 14,13
– 28,9092 = 14,13
r =  =
=  = 0,82
= 0,82
або
r =  σ х =
σ х = 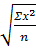 – (
– ( )2 =
)2 =  = 3,922
= 3,922
σу = 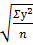 – (
– ( )2 σу
)2 σу  = 3,759
= 3,759
r =  =
=  = 0,82
= 0,82
Для лінійної форми зв'язку коефіцієнт кореляції коливається від 0 до + 1.
Квадрат коефіцієнта кореляції характеризує частина загальної варіації, викликану досліджуваним фактором. Квадрат коефіцієнта кореляції і. носить назву коефіцієнта детермінації:
r2 = 0,822 = 0,6724.
У зв'язку з тим, що точність результатів вивчення кореляційних зв'язків значною мірою залежить від кількості зіставляються даних, яке часто буває обмеженим, вельми корисно вимір похибки (суттєвості) обчисленого коефіцієнта кореляції і кореляційного відношення.
Істотність r і ŋ перевіряють по t –критерієм (2.32).
T =  , а σr =
, а σr = 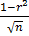 , (2.32)
, (2.32)
де σr - середня квадратична помилка коефіцієнта кореляції;
r - коефіцієнт кореляції;
n - число спостережень
При ймовірності судження р = 0,99, = 2,8188  , фактичне відношення коефіцієнта кореляції до середньої квадратичної помилку склало 11,7 - зв'язок достовірний.
, фактичне відношення коефіцієнта кореляції до середньої квадратичної помилку склало 11,7 - зв'язок достовірний.
Тепер розглянемо другий метод вирішення даної системи:
22 а + 773,5 в =636
773,5 а + 27533,95 в =22627,12
Цю систему зручно вирішувати за допомогою визначників. Для цього обчислюються значення трьох визначників другого порядку:
1) для системи, складеної з коефіцієнтів при а і в
△= 22 773,5 = 7444,65
773,5 27533,95
22 × 27533,95 – 773,52 = 7444,65.
2) для системи, в якій стовпець коефіцієнтів при, а замінений стовпцем вільних членів:
636 773,5
△о = = 9514,38
22627,12 27533,95
3) для системи, в якій стовпець коефіцієнтів при в замінений стовпцем вільних членів:
22 636
△1 == 5850,64
773,5 22627,12
а =  =
= 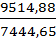 = 1,274.
= 1,274.
Тоді:
в =  =
=  = 0,786
= 0,786
Кореляційне рівняння має вигляд:
у = 1,274 + 0,786
R = 0.82, R2 = 67%
Достовірність коефіцієнта оцінюється зазвичай за допомогою F - критерію, обчислюваного за формулою (2.34):
F =  , (2.34)
, (2.34)
де р - кількість параметрів рівняння регресії.
F =  = 40,6
= 40,6
Оскільки обчислене значення F більше табличного (40,5 ≥ 4,35), є підстави визнати достовірним значення коефіцієнта кореляції.
Рівняння регресії (у = 1274 х 0786) можна використовувати для прогнозування продуктивності корів.
Приклад: Встановити вплив на надій корів рівня годівлі та яловості. Аналіз даних показує, що це зв'язок прямо пропорційний (табл. 2.5).
Таблиця 2.5
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 719; Нарушение авторских прав?; Мы поможем в написании вашей работы!