Надій, витрати кормів, отримано телят по господарству

№ хозяйств	Вихідні дані	Розрахункові величини
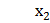
Надій на корову, ц у	Витрати кормів на корову за рік, ц. корм. од. х1	Отримано телят на корів	ух1	ух2	х1х2	х1^2
1.	24,9	32,9		819,21	1824,6	2434,6	1082,41
2.	25,9	34,7		898,73	2149,7	2880,7	1204,09
3.	29,4	37,8		1111,32	2381,4	3061,8	1428.84
4.	26,3	33,6		883,68	2314,4	2956,8	1128,96
5.	25,8	30,7		792,06	2296,2	2732,3	942,49
6.	27,2	33,3		905,76	2284,1	2797,2	1108,89
7.	24,5	29,7		727,65	2156,0	2613,6	882,09
8.	29,0	36,1		1046,9		3068,6	1303,21
9.	35,5	39,9		1416,45	2946,5	3311,7	1592,01
	31,1	35,6		1107,16	2892,3	3310,8	1267,36
11.	25,1	33,6		843,36	2033,1	2721,6	1128,96
	39,1	46,8		1829,88	3010,7	.3603,6	2190,24
	29,4	36,8		1081,92	2440,2	3054.4	1354,24
	24,8	31.9		791,12	2083,2	2679,6	1017,61
	28,0	34,0					1156,00
	33,1	38,8		1284,28	3012,1	3530,8	1505,44
	26,9	38,4		1032,96	2152,0		1474,56
	21,2	30,2		640,24	1653.6	2355,6	912,04
	28,2	36,7		1034,94	2086,8	2715,8	1346,89
	24,3	29,6		719,28	2016.9	2456,8	876,16
	32.1	38,5		1235,85	2953,2	3542,0	1482,25
	28,1	32,9		924,49	2781,9	3257,1	1082,41
Σ	619,9	772,5		22079,24	52416,6	65148,7	27467,25
х	28,2	35,1	84,5	1003,6	2382.5	2961,3	1248,5

Форма залежності між надоєм і рівнем годівлі та виходу телят (2.35):

y = a + вх₁ + сх_2, (2.35)

де у - удій на фуражну корову, кг;

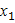- витрата кормів на корову в рік, ц корм. од.;

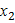- вихід телят на 100 корів;

а, в,с - невідомі параметри рівняння, які визначаються з наступної системи (2.36):

Σ у =na + в Σ х₁ + c Σ х₂

Σ х₁у =а Σ х₁ + в Σ х₁² + c Σ х₂х₂ (2.36)

Σ х₂у =а Σ х₂ + в Σ х₁х₂ + c Σ х₂²

або

619,9 = 22 а +772,5 в + 1858 с

22079,24 = 772,5 а + 27467,15 в + 65148,7 с

52416,6 = 1858а + 65148,7 в + 157728 с

Вирішивши цю систему, ми знаходимо с = 0175, в = 0936, а = -19469.

Зв'язок між надоєм (у) рівнем годівлі (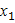) і виходом телят (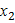) виразиться наступним рівнянням (2.37):

у = − 19,469 + 0,936 х₁ + 0,175 х₂ (2.37).

Таким чином, коефіцієнт при 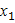(в = 0,936) показує, що при збільшенні витрати кормів на 1 ц надій підвищується на 0,936 ц.

Коефіцієнт при 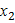показує, що при збільшенні виходу телят на 1 голову надій на корову підвищується на 0,175 ц.

З цього рівняння можна визначити удій, якщо відомі витрата кормів (40ц корм. од.) і вихід телят (98 гол.):

у = −19,469 + 0,936 × 40 + 0,175 × 98 = 35,12 ц

Удій на корову буде складатимо 3512 кг молока.

Алгоритм моделювання виробничої функції за допомогою спеціалізованого математичного пакету STATISTCA на ПЕОМ наведено у додатку 8.

2.10. Структура математической модели лінійного програмування (ЛП)

Математична модель ЛП є комбінацією наступних складових:

● змінних (вхідних і вихідних) - завжди мають область

визначення;

● параметрів - набувають числових значень;

● функціональних залежностей;

● обмежень (штучних і природних);

● цільових функцій (у завданнях оптимізації).

В якості своєрідного інструменту для побудови математичних моделей ЛП виступають таки математичні символи і знаки невідомі змінні позначають останніми буквами латинського алфавіту (Х₁, Х₂,… Х_1j), а відомі – першими буквами алфавіту (a₁,b₁,c_1j).

Для наповнення моделі конкретним змістом розробляють параметри – вільні члени, техніко - економічні коефіцієнти і коефіцієнти лінійної форми - критерії оптимальності.

Вільні члени - це параметри, не змінні за заданих умов (об’єми наявних виробничих ресурсів: сільськогосподарських угідь, робочої сили, техніки, кормів, грошових коштів). Їх реальна наявність включається в модель за фактичними або планованими даними.

Основні змінні: поголів’я тварин, площі посіву кормових культур, потужність обладнання, поживність раціону, валове виробництво молока тощо.

Додаткові змінні показують надлишок чи нестачу над правою частиною, тобто наявність ресурсів. Виробничі ресурси: тварини, земля, техніка, затрати

праці, корми завжди обмежені. Для кожної змінної величини встановлюють розмірність, яка залишається незмінною до завершення всіх розрахунків.

Тому математична модель становить сукупність різноманітних обмежень. На змінні накладаються обмеження.

Обмеження − запис умови задачі у вигляді нерівності або рівняння.

Усі обмеження класифікуються на основні, додаткові й допоміжні.

Основні обмеження – це тварини, земля, трудові ресурси, фінанси, енергоносії, корми, обладнання, техніка. Наприклад, обмеження щодо використання кормових одиниць раціону має вигляд (2.38):

х₁ + 0,5х₂ + 0,2х₃ + 0,36х₄ + 0,2х₅ + 0,12х₆ > 8,6(2.38).

Додаткові обмеження: споживання кормів окремими групами тварин, граничні розміри посівних площ, рівень концентрації тварин, потужність обладнання тощо. Наприклад, обмеження по кількості силосу в раціоні для корови: х₃ > 20.

Допоміжні обмеження вводять тільки для полегшення розробки розгорнутої математичної моделі, правильного відображення всіх економічних зв'язків, закономірностей. Так, допоміжним обмеженням в моделях з оптимізації раціонів для худоби є обмеження по точному кількістю кормових одиниць раціону (2.39):

х₁ + 0,5х₂ + 0,2х₃ + 0,36x₄ + 0,2х₅ + 0,12x₆ = х₇, (2.39)

де х₇− допоміжна змінна, яка означає точну кількість кормових одиниць в раціоні.

Параметри задачі ЛП є вільні члени або постійні величини (константи) (в_j,), технолого - економічні коефіцієнти (а_ij) і коефіцієнти оцінки змінних в цільовій функції (оцінки, ціни) (С_J). Вільні члени (константи) розраховують у зв'язку і з умовами постановки завдання. Це можуть бути величини, що характеризують обсяг виробничих ресурсів, або величини по гарантованого обсягу виробництва. У моделях з оптимізації раціонів - норма поживних і біологічно активних речовин.

Teхніко - економічні коефіцієнти (коефіцієнти при невідомих в обмеженнях) - це постійні величини, що не змінюються за даних умов (норми витрат виробничих ресурсів, норми задоволення потреб, вихід продукції на одиницю вимірювання кожного виду і способу виробничої діяльності). Часто їх називають коефіцієнтами витрат - випуску. Це норми затрат праці і засобів виробництва, вміст поживних речовин в кормах, урожайність культур, продуктивність тварин. Маючи прямі техніко - економічні коефіцієнти, можна розрахувати похідні: вихід продукції з 1га в грошовому виразі; вартість продукції, отриманої від 1 голови тварин за рік; вихід кормів з 1га землі і тому подібне. Техніко - економічні коефіцієнти можуть бути фактичними або нормативними, представленими в натуральному або грошовому виразі.

Нормативні коефіцієнти означають норми витрат виробничих ресурсів або норми задоволення потреб на одиницю виміру по кожному виду і способу виробничої діяльності і характеризують технологічні залежності в планово -економічних задачах.

Коефіцієнти пропорційності вводяться в матрицю за додатковими і допоміжним обмеженням. При описі додаткових умов технологічної проблеми зустрічаються умови питомої вагі певного виду корму у складі кормів іншої групи, співвідношення полів сівозміни і т. п. Приклад, корми х₁ може становити від складу раціону не більше 1/3. У раціон входить два корму х₁ і х₂ (2.39 ).

х₁ ≤ (Х₁+Х₂). (2.39)

Перетворимо цю нерівність (2.40):

Х₁ – X₁ ≤ Х₂; (2.40)

Х₁ ≤ Х₂;

2Х₁ ≤ Х₂;

2Х₁ − Х₂ ≤ 0.

Значення 2 і буде коефіцієнтом пропорційності для X₁.

Коефіцієнти при змінних у функції мети, які є критерієм оптимальності, (вихід продукції, дохід, витрати засобів на одиницю вимірювання кожного виду і способу виробничої діяльності). Вони можуть бути натуральними і вартісними. Для отримання більш менш достовірних оцінок доцільно проаналізувати у господарстві фактичні середньореалізаційні ціни за декілька років.

Оптимізація технологічного процесу означає, що знайдено максимальне чи мінімальне значення критерію оптимальності (максимум валової чи товарної продукції, прибутку; мінімум витрат кормів, енергоносіїв, людино/ годин тощо).

Дата добавления: 2014-11-29