Матриця моделі

Наймінування обмежень	Зміни та їх значення	Объєм ресурсів та тип обмежень
Х1	Х2	Х3	…	Хn
1.	а11	а12	а13		а1n	≥ ≤ B1 =
2.	а21	а22	а23		а2n	≥ ≤ B2 =
…
…
…
m	am1	am2	am3		amn	≥ ≤ Bm =
Наймінування цільової функції	C1	C2	C3		Cn	→max (min)

Розглянемо приклад: нехай підприємство виробляє два види продукції: P₁ і P₂, для яких використовують сировину (ресурси) s₁ і s₂. Вартість одиниці кожного продукту відповідно C₁ і C₂: C₁ = 3 од., C₂ = 2 од. Знайти скільки треба виробити продукції P₁ і P₂, щоб отримати max доход

F → max) (і вкластися в обмеження по сировині: для s₁використати не більше b₁ =≤ 12 ресурсів; для s₂ - не більше b₂ =≤ 10 ресурсів і по

забрудненню середовища: не більше ≤ b₃ = 6 доз.

Далі витрат сировини та забруднення середовища при виробництві одиниці продукту відповідно:

Р₁ Р₂

S₁ a₁₁= 6 a₁₂= 3

S₂ a₂₁= 2 a₂₂= 4

Забруднення a₃₁= 2 a₃₂= 0

Формалізуємо задачу у вигляді таблиці для зручності побудови математичної моделі. Припустимо, що x₁ - кількість продукту P₁; x₂ - кількість продукту P₂:

Ресурс	x 1	x 2	Обмкження b 1
S 1			≤ 12
S 2			≤ 10
Забруднення			≤ 6
F

Структурна модель:

F_max =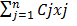

a₁₁x₁ + a₁₂x₂ ≤ b₁

a₂₁x₁ + a₂₂x₂ ≤ b₂

a₃₁x₁ + a₃₂x₂ ≤ b₃

x₁≥ 0, x₂≥ 0

Розгорнута числова модель:

F = 3х₁ + 2х₂

6х₁ + 3х₂ ≤ 12

2х₁ + 4х₂ ≤ 10

2х₁ + 0х₂ ≤ 6

x₁≥ 0, x₂≥ 0

По відношенню до параметру годині моделі технологічних процесів поділяють на детерміновані та стохастичні.

У детермінованих моделях процеси описується аналітичними виразами, скоріш всього системами дифференціальних або алгебраїчних рівнянь.

У стохастичних моделях процеси описується стохастичними рівненнями фізичний сенс мають не окремі реалізації процеса, а сукупність реалізацій і їх параметри(математичне очікування, дисперсія, кореляційні залежності та ін.). Ефективність стохастичних моделей у значній мірі визначається якісним виконанням усіх етапів експерименту (висунення гіпотези, планування, проведення досліду, обробка результатів та ін.).

У межах тваринницького підприємства математичні методи використовують за двома основними напрямками: регулювання технологічних процесів та оптимізація управління. Уся сукупніость розв'язання екстремальних завдань називається математичним або оптимальним програмуванням. Термін "програмування" означає обчислення певних характеристик досліджуванного об' єкту або процесу з метою управління їх станом (змінами) з використанням відповідної математичної моделі.

У математичному програмуванні виділяють такі основни розділи: лінійне програмування (ЛП), якщо ММ подається лише лінійними функціональними залежностями та нелінійне програмування, якщо при розбудові ММ використовуються нелінійні функціональні залежності.

При організації і плануванні виробництва продукції тваринництва застосовуються наступні групи математичних моделей.

Управління запасами. Запас - це ресурс можливості виконання будь-якого замовлення. Із збільшенням запасів створюються умови для більш ритмічної роботи виробництва. Якщо запасів не вистачає, то можливі значні збитки за рахунок невиконання зобов’язань. Але разом iз збільшенням запасів збільшується мертвий капітал i витрати на зберігання. Виникає проблема управління запасами при найменших витратах.

Розподіл ресурсів. Ресурси – це гроші, генетичний потенціал тварин, корма, матеріали, людська праця i т.п. Ресурси завжди обмежені i в різних виробах забезпечують різний прибуток. Виникає проблема розподілу людей, матеріальних та інших ресурсів між виробами з метою отримання найбільшого прибутку.

Ремонт та заміна технологічного обладнання. Застаріле обладнання вимагає витрат на ремонт i має знижену потужність. Потрібні розрахунки для прийняття рішення щодо темпів ремонту та заміни обладнання, які забезпечують найбільший прибуток.

Задачі масового обслуговування. Розглядають питання створення та функціонування черг (в технологічному процесі, у зоні діяльності підприємства, лінійно - ротаційне схрещування). Потрібно розв’язати проблеми якісного обслуговування (використання) при мінімальних витратах на обладнання.

При вирішенні виробничих завдань ставиться певна мета, яку необхідно досягнути. При цьому ми маємо обмежену кількість ресурсів. Тому, виникає проблема вибору із багатьох варіантів рішення того варіанту, що забезпечує найкращий розподіл ресурсів.

Модель завжди наповнена конкретним економічним змістом, "прив’язана" до визначеної проблеми виробництва. Вибір оптимального варіанту визначається показником, який називають критерієм оптимальності.

Дата добавления: 2014-11-29