Витрати ресурсів на виробництво одиниці кожного виду продукції

Вид ресурсу	Вид продукції	Загальний обсяг ресурсу
А	В
І
ІІ
ІІІ

Ціна реалізації одиниці продукції виду А становить 20 грн., проте прибуток залежить від витрат на виробництво, які пропорційні квадрату кількості виготовленої продукції. Аналогічно визначається прибуток для продукції виду В, ціна реалізації якої дорівнює 18 грн.

Розв’язання. Позначимо через х ₁ кількість продукції виду А, х ₂ - кількість продукції виду В, тоді загальний прибуток матиме вигляд:

.

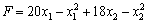Математична модель задачі має вигляд:

,

.

Розв’яжемо задачу методом Франка Вульфа.

І ітерація.

Вибираємо точку, що належить множині допустимих планів задачі.

Розглянемо, наприклад, точку:

.

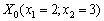Визначимо градієнт цільової функції:

.

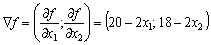В точці

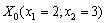
обчислюємо значення градієнта:

.

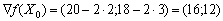Використовуючи розраховане значення градієнта, записуємо і вводимо нову цільову функцію:

.

Маємо таку задачу лінійного програмування:

.

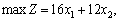
Розв’язуючи цю задачу симплексним методом, знаходимо її оптимальний план: .

Знайдемо новий допустимий план задачі, використовуючи формулу

для визначення координат наступної точки.

Визначаємо координати точки Х ₁:

, ,

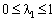Знайдемо крок 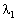такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х ₁, х ₂, які виражені через 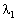, у цільову функцію:

:

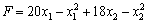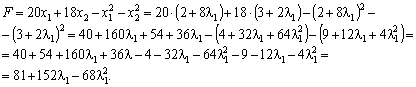
Отримали функцію, що залежить від 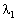. Знайдемо значення 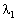, за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:

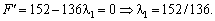
Оскільки 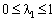, то беремо 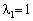. Тоді наступна точка Х ₁ має координати:

.

Для знайденої точки:

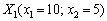
обчислюємо значення цільової функції: .

ІІ ітерація

Узявши точку:

,

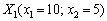обчислюємо значення градієнта в ній:

Використовуючи розраховане значення градієнта, вводимо нову цільову функцію: .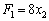

Отримуємо таку задачу лінійного програмування:

.

Розв’язавши її симплексним методом, отримуємо оптимальний план:

.

За формулою визначаємо координати наступної точки наближення. Визначаємо координати точки Х ₂:

,

.

Знайдемо такий крок λ₂, за якого досягається максимальне значення цільової функції:

Матимемо: .

Обчислимо координати наступної точки Х ₂:

Для знайденої точки:

значення цільової функції дорівнює:

.

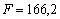Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку і переконуємося, що значення цільової функції знову зростає: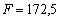

На IV ітерації розраховуються координати точки:

,

для якої .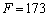

V ітерація

Узявши точку , обчислюємо значення градієнта в ній:

.

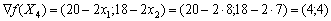Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію: 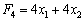і маємо таку задачу лінійного програмування:

,

.

Розв’язавши цю задачу, отримаємо значення оптимального плану , тобто повертаємося до попереднього значення. Отже, точку з координатами 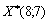вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.

Дата добавления: 2014-11-29