Алгоритм рішення транспортні за допомогою надбудови „Поиск решения” у MS Excel

Потреби та її запаси сировині

Побудова числової математичної моделі

Матриця відстаней між постачальниками та споживачами корму

Поставщики (скирти)	Споживачі (ферми)	Наявність, т
Потреба, т

Перелік змінних величин та їх умовні позначення наведени у вигляді робочої таблиці транспортної задачі (табл. 2.28).

Таблиця 2.28

Робоча таблиця транспортної задачі

Постачальники (скирти)	Споживачі (ферми)	Наявність, т (Ai)
	Х11 ; С11	Х12 ; С12	Х13 ; С13	А1
	Х21 ; С21	Х22 ; С22	Х23 ; С23	А2
	Х31 ; С31	Х32 ; С32	Х33 ; С33	А3
	Х41 ; С41	Х42 ; С42	Х43 ; С43	А4
Потреба, т (Вj)	В1	В2	В3	В

Математична модель транспортної задачі (закритого типу) матиме наступний вигляд:

Сmin = (Х₁₁ + 2Х₁₂ + Х₁₃) + (4Х₂₁ + 2Х₂₂ + 3Х₂₃) + (2Х₃₁ + Х₃₂ +

+ 4Х₃₃) + (5Х₄₁ + 2Х₄₂ + 3Х₄₃)

Кожний доданок являє собою використання тарифа по данному маршруту на кількість перевезеного по ньому вантажу.

Сформулюємо умови обмеження задачі (вивезення –ввезення вантажу):

Х₁₁ + Х₁₂ + Х₁₃ = 140

Х₂₁ + Х₂₂ + Х₂₃ = 130

Х₃₁ + Х₃₂ + Х₃₃ = 80

Х₄₁ + Х₄₂ + Х₄₃ = 10

Х₁₁ + Х₂₁ + Х₃₁ + Х₄₁ = 160

Х₁₂ + Х₂₂ + Х₃₂ + Х₄₂ = 50

Х₁₃ + Х₂₃ + Х₃₃ + Х₄₃ = 150

Третя умова – незаперечності невідомих – являє собою систему з 12 нерівностей (m×n).

Х₁₁> 0; Х₁₂> 0; Х₁₃> 0; Х₂₁> 0; Х₂₂> 0; Х₂₃> 0;

Х₃₁> 0; Х₃₂> 0; Х₃₃> 0; Х₄₁> 0; Х₄₂> 0; Х₄₃> 0

Приклад 2. Чотири молокозаводи для виробництва продукції використовують сировину, яка надходить із трьох ТОВ. На кожен завод сировина може завозитися з будь-якого ТОВ. Потреби в сировині кожного із заводів, запаси сировини та тарифи перевезень наведені у таблиці 2.29. Скласти такий план перевезень, при якому загальна вартість перевезень є мінімальною.

Таблиця 2.29

ТОВ	МОЛОКОЗАВОДИ	ЗАПАСИ
І		ІІІ	ІV
І
ІІ
ІІІ
ПОТРЕБИ

Нехай існує [m] пунктів, у яких зосереджено деякий однорідний вантаж. Номер пункту зосередження [i] = 1, m. Нехай відома кількість вантажу, що знаходиться у кожному пункті зосередження [a_i]. Цей вантаж треба доставити до [n] пунктів споживання. Номер пункту споживання [j]=1,n. Нехай відома потреба [b_ij ] у цьому вантажі у кожному пункті споживання. Також відомі питомі витрати на перевезення вантажу з i-того пункту зосередження до j-того пункту споживання [c_ij]. Треба визначити, скільки вантажу треба везти з кожного з пунктів зосередження до кожного з пунктів споживання таким чином, щоб з кожного пункту зосередження загалом вивозилося не більше, ніж там є, а до кожного пункту споживання не менше від потреби (), і загальна вартість перевезень була якомога меншою.

Розв’язок задачі:

Позначимо невідомі обсяги перевезень з кожного пункту зосередження до кожного пункту споживання [x_ij]. Отже, умова про те, що загальна кількість вантажу, вивезена з кожного пункту зосередження, не перевищує кількість вантажу в ньому:

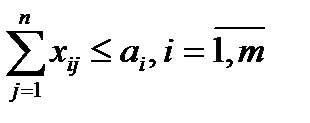
Умова про те, що потреба кожного пункту споживання має задовільнятися:

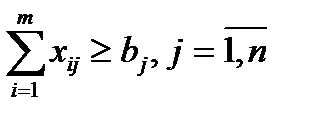
Обсяги перевезень між кожним пунктом зосередження і споживання – невід’ємні величчини:

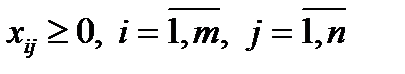
Розглянуті нерівності визначають деяку множину, до якої належить багато варіантів перевезень. Серед цих варіантів треба обрати такі, що мінімізували б функцію:

(пошук умовного мінімуму для функції багатьох змінних).

Для перевірки оптимальності складеного плану перевезень скористаємося надбудовою „ Поиск решения ” MS Excel (рис. 2.8 і ріс. 2.9).

До комірки F10 внесено формулу = СУММ(B10:E10) і простягнуто її до комірки F13, до комірки В14 внесено формулу = СУММ(B10:B13) і простягнуто її до комірки Е14. До цільовій комірці G14 введено формулу у вигляді виразу = СУММПРОИЗВ(B4:E7;B10:E13).

На рис. 2.8 наведено внесення обмежень моделі у діалоговому вікні надбудови „ Поиск решения ”.

Розрахуємо середню вартість:

Рис. 2.8 Вікно значення зміних задачі

Рис. 2.9. Вікно обмежень моделі

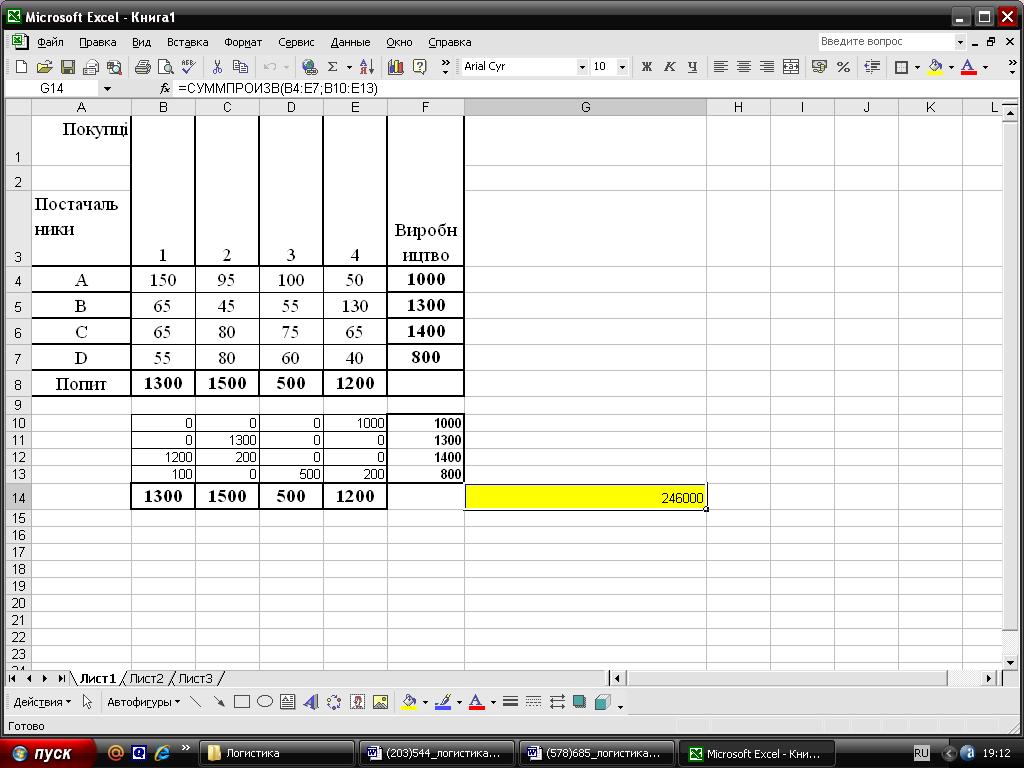
Рис. 2.10. Заключне рішення задачі

Як бачимо, останній план значно краще, вартісь перевезення вантажу скоротилася на 23,11 грн.

Математична модель буде мати наступний вигляд:

Дата добавления: 2014-11-29