Моделювання та оптимізація технологічних задач транспортного типу

Розподільчі (транспортні) задачі - окремий випадок загальних задач лінійного програмування.

Розподільчі задачі- це задачі по розподілу ресурсів, а транспортні - по перевезенню вантажів. Найбільш простий вид транспортної задачі – перевезення однородного вантажу одним видом транспорту.

Транспортна задача може бути закритого типу, якщо сумарна наявність вантажу всіх поставщиків рівне сумарній потребі в грузі всіх споживачів і відкритого типу, якщо ця рівність невиконується (т.е. A ≠ В). Транспортна задача відкритого типу може бути перетворена в транспортну задачу закритого типу. При цьому можливі два випадки:

1. якщо А >B (пропозиція випереджає попит), тобто сумарна наявність вантажу більше сумарної потреби в ньому. Толи у умови задачі вводиться «фіктивний» (n + 1) – й споживач, приписується споживач в вантажу В_{n + 1} = А – В. Введення додаткового споживача рівносильно збільшенню робочої таблиці на один стовпчик. При цьому, тарифи на доставку одиниці вантажу до споживача приймаються рівними нулю, тому як, вантаж «фіктивному» споживачу – В доставляться не буде).

2. якщо А < В (попитперенбільшує пропозіцію), тобто сумарна потреба у вантажі більше, ніж сумарна його наявність. Тоді в умови задачі вводиться «фіктивний» (m + 1) постачальник з наявістю у нього А_{m + 1} = В – А одиниць вантажу, а в рабочу таблицю додається (m + 1) –ю рядок, вважаючи тарифи у цьому рядку рівними нулю.

Основними властивостями транспортної задачі є:

1.Система основних обмежень являє собою систему з (m + n) рівнянь з

(m × n) невідомими;

2.Коефицієнти при невідомих в системі обмежень –одиниці;

3.Кожна невідома входить в два рівняння, в матриці в кожному стопчику по рядках обмежень находим по дві одиниці.

4.В системі із m ×n обмежень одне рівняння може бути скорочено, оскільки воно є наступником останніх. Тому, в системі обмежень досить (m + n – 1) рівнянь. Крім того, транспортна задача закритого типу завжди має розвязок.

Постановка задачі та підготовка вихідної інформації

Умови транспортної задачі формулюються наступним чином. Визначити такий маршрут транспортування вантажу, при якому загальні витрати на його перевезення були б мінімальними при умовах, що однорідний вантаж А, що зберігається на декількох пунктах (1, 2,…, m) в кількостях відповідно, А₁, А₂, …, А_m одиниць А = А₁ + А₂ + … + Аm необхідно доставити в n заданих пунктів призначення (1, 2,…,n), споживаючих його в кількостях В₁, В₂, …, В_n (В = В₁ + В₂ + … + Вm). Вартість перевезення одиниці вантажу з i пункта наявності в j пункт споживання ддорівнює Сij, а відповідну кількість одиниць вантажу позначимо через Хij (i=1,2,…j = 1, 2,n), споживаючих його в кількостях В₁,В₂,…,В_n.

Кожна величина Cij, названа тарифом і є відомою величиною. Значення Хij є невідомою. Звідси, якщо сумарна наявність вантажу у поставщиків позначити через А, тоді:

А = А₁ + А₂ + А₃ + … + Аm = .

Аналогічно, сумарна потреба в вантажі споживачів(В) складає:

В = В₁ + В₂ + В₃ + …+ Вn = .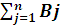

У випадку, коли сумарна наявність вантажу усіх поставщиків рівна суммарній потребі усих споживачів, дотримується умова:

А = В ( = ),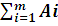

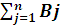транспортна задача вважається закритого типу, якщо ця рівність не виконується (тобто А ≠ В) відкритого типу.

Дата добавления: 2014-11-29