Оценка сомнительных результатов

Допустим, получили результаты из одной генеральной совокупности, для которой некоторые результаты выборки вызывают сомнение. Возникает вопрос: какие наблюдения оставить в выборке, а какие выбросить? Для решения данной задачи существует ряд критериев. Рассмотрим их на примерах.

1 Провели пять выстрелов из гаубицы, имеем следующий ряд точек попадания снарядов по дальности [M]

L: 3200; 3225; 3230; 3245; 3600.

Подозрительным является результат 3600 м. Если данный результат находится в пределах для нормального распределения, то мы имеем м, а м. Если результат 3600 исключить из выборки как аномальный, то получим следующие оценки: м, а м. Как видим, среднее квадратичное (сигма) отличается на порядок.

1 Критерий об оценке сомнительных результатов предполагает, что 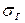- генеральной совокупности известная величина. Вводится статистика

.

Данная статистика распределена не по нормальному закону, но похожа на нормальный закон (рисунок 2.9).

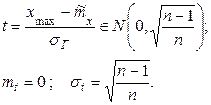
Нормируем случайную величину

.

Запишем через нормальный закон распределения вероятность попадания в критическую область

.

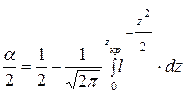Рисунок 2.9 – Нормальный закон распределения

По заданному уровню значимости находим (смотреть приложение Д). Рассчитываем опытное значение. Если , то сомнительный результат отбрасывается

2 Если генеральной совокупности неизвестно, то в этом случае вводим статистику, которая принадлежит критерию Смирнова – Гребса

.

Распределение Смирнова – Гребса имеет оценку

.

В таблице имеем такую оценку

.

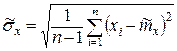Для перехода к распределению Смирнова – Гребса все результаты надо увеличить на . Для нашего примера:

,

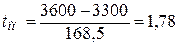табличное критическое значение равно .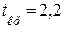

Получили опытное значение меньше критического, значит, подозрительный результат следует оставить в выборке.

3 Распределение Смирнова – Гребса по одному выбросу.

Вводится статистика Гребса

,

где – среднее по всей выборке;

– среднее по выборки без сомнительного результата.

Если 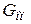попадает в критическую область, то аномальный результат отбрасываем.

4 Статистика Титьена – Мура позволяет проводить оценку сразу нескольких выбросов. Определяется опытное значение:

где – среднее по всей выборке;

– среднее по выборке без к выборочных сомнительных результатов.

Оценка Титьена-Мура имеет большое распределение, входом в таблицу является 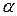, количество выбросов k и объем выборки n.

Пример № 6. Имеются данные – временные затраты на выполнение однотипных работ для десяти человек (таблица 2.4).

Таблица 2.4

Количество человек
Время выполнения

Нет информации о значениях математического ожидания и дисперсии . Есть ли основание для исключения последнего результата из выборки. Проведем оценки по следующим критериям:

1 По критерию Смирнова определяем опытные значения

Если выбрать , то по таблице Смирнова (приложение З) .

Вывод: Результат – проходит с малой надежностью.

2 По критерию Гребса имеем

,

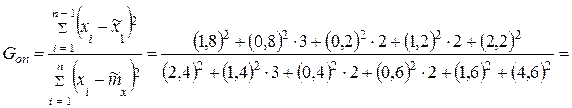
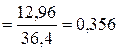где

При уровне значимости по таблице Гребса (приложение Е) определяем критическую область . Функция Гребса представлена на рисунке 2.10.

Рисунок 2.10 – Функция Гребса

По критерию Гребса результат также проходит с малой надежностью.

3 По критерию Титьена-Мура проверим следующие результаты:

а) если выбросить последний результат , то получим .

По таблице Титьена-Мура (приложение Ж) при 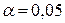находим критическое значение следовательно, результат необходимо выбросить, а при получаем , поэтому результат нужно оставить.

б) Определим опытное значение статистики Титьена-Мура

,

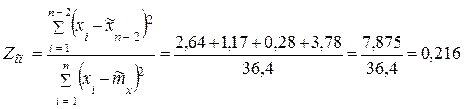где .

Из таблицы для количества выбросов определяем критические значения статистики для различных уровней значимости .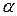

При ; при ; при

Вывод: при и – результат 15 и 18 необходимо выбросить из выборки. Если , то результаты 15 и 18 необходимо оставить.

Дата добавления: 2014-11-29