Оценка равенства дисперсий двух выборок

Имеем две выборки объёмом n и m.

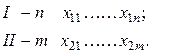
Оценки дисперсий будут иметь вид

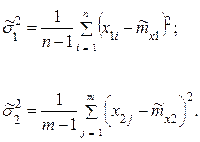
Выдвигается гипотеза о равенстве дисперсий .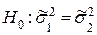

Вводим статистику

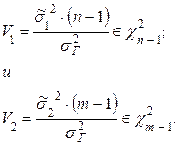
Рассмотрим отношение

.

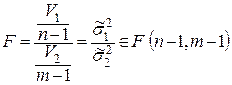Данное отношение дисперсии принадлежит распределению Фишера со степенями свободы n – 1 и m – 1. Рассмотрим на примере односторонний критерий.

Пример № 5. Имеем две выборки n₁ = 11 и n₂ = 14. Найденные оценки дисперсии равны 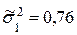и 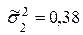. Необходимо при уровне значимости α = 0,05 проверить гипотезу

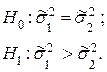
По заданному 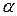найдем F критическое для n – 1 и m – 1. Из таблицы Фишера F _кр(10,13) = 2,67 определяем:

,

следовательно 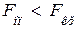, поэтому опытные данные не противоречат гипотезе Н₀. Возьмем уровень доверительной вероятности 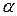= 0,1. По таблице Фишера (приложение В) F (10, 13) = 2,14. Следовательно, гипотеза Н₀ принимается (рисунок 2.7).

Рисунок 2.7 – Распределение Фишера для одностороннего критерия

Рассмотрим двусторонний критерий. Для этого α = 0,1 делим пополам. Для двустороннего критерия выдвигаем две гипотезы

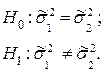
Если оценка попадает внутрь интервала, то исходные данные не противоречат гипотезе Н₀.

Для двустороннего критерия мы имеем следующую статистику Фишера.

Рисунок 2.8 – Распределение Фишера для двустороннего критерия

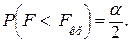
По таблице Фишера определим:

,

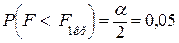Поэтому

,

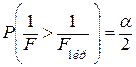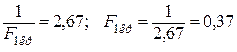– левый интервал.

Получили двусторонний интервал меньше 0,37 и больше 2,67. Наша оценка находится в интервале принятия решения.

Дата добавления: 2014-11-29