Статистическая проверка гипотез

Определить положение центра группирования и доверительный интервал J с надежностью b.

Пример № 3. Имеем выборку.

Таблица 2.2

N
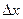
	-10				-5		-10

1 Определим оценку математического ожидания

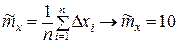м.

2 Оценка среднего квадратического отклонения

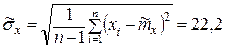м.

3 Оценка среднего квадратического отклонение математического ожидания

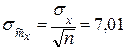м.

4 Доверительный интервал определяется с помощью таблиц распределения Стьюдента по формуле:

.

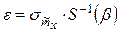5 Число степеней свободы равно n-1=9. Из таблицы Стьюдента определяем:

тогд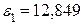а , а 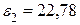, то есть при 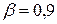оценка 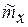попадает в интервал, J₁ 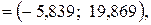а с надежностью 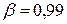имеем интервал J₂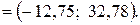

Если оценку проводить не по закону Стьюдента, а по нормальному закону то получим следующие результаты.

При 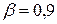t_b= 1,643, при 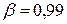t _b=2,576.

Ошибка в определении интервала e при 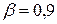11.26/12.89 составляет 13 %, при 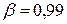18,06/22,79 составляет 12 %.

С теорией статистического оценивания параметров тесно связана проверка статистических гипотез. Она используется всякий раз, когда необходим обоснованный вывод о преимуществах того или иного способа инвестиций, измерений, стрельбы, технологического прогресса, об эффективности нового метода обучения, управления, о пользе вносимого удобрения, лекарства, об уровне доходности ценных бумаг, о значимости математической модели и т.д.

Определение. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Различают простую и сложную статистические гипотезы. При простых гипотезах обязательно известен закон распределения исследуемой случайной величины и оценка математического ожидания строго равна табличному значению. При проверке сложных гипотез не известен закон распределения случайной величины, и нет строгого равенства между табличным значением и оценкой математического ожидания.

Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают 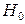. Наряду с нулевой гипотезой 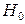рассматривают альтернативную, или конкурирующую, гипотезу 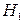, являющуюся логическим отрицанием 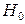. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез. Правило, по которому гипотеза 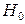отвергается или принимается, называется статистическим критерием или статистическим тестом.

Все проверки гипотез дают ответ с определенной степенью надежности. Для этого задается уровень значимости.

Определение. Вероятность 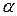допустить ошибку 1-го рода, то есть отвергнуть гипотезу 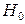, когда она верна, называется уровнем значимости критерия.

Вероятность допустить ошибку 2-го рода, то есть принять гипотезу 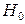, когда она неверна, обычно обозначают .

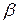Определение. Вероятность 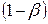не допустить ошибку 2-го рода, то есть отвергнуть гипотезу 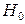, когда она неверна, называется мощностью (или функцией мощности) критерия.

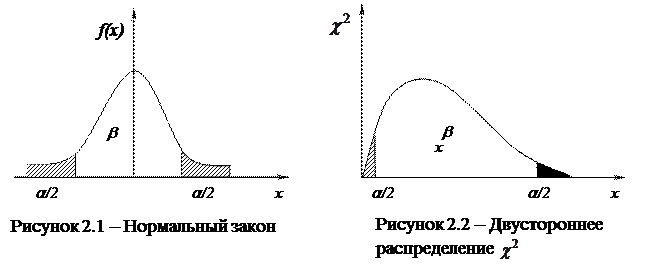
Различают двусторонний критерий и односторонний. При двустороннем критерии назначается доверительная вероятность, и отсекаются «хвосты» нормального распределения, то есть они для нас незначимы.

Если рассматриваем статистику 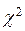(хи-квадрат), то тоже имеем два «хвоста», которые для нас незначимы (рисунки 2.1, 2.2).

Если изменение физической величины происходит только в одну сторону, то необходимо рассматривать односторонний критерий (рисунок 2.3).

Уровень значимости α это число, дополняющее доверительную вероятность b до единицы. Доверительная вероятность, это синоним надежности, или по-другому степень уверенности.

Значимость с точки зрения проверки гипотезы означает принять гипотезу с определенной уверенностью или отвернуть ее, если оценка попадает в интервал не принятия гипотезы.

Для проверки гипотез вводится случайная величина, для которой обязательно известен закон распределения. Эта случайная величина практически реализуется на интервале, который мы будем разделять на зону принятия и не принятия гипотезы. Чтобы указать эту зону не принятия гипотезы, задаем уровень значимости 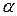. При этом если критерий односторонний, то .

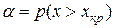Для двустороннего критерия имеем:

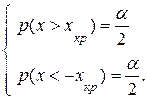
Если результат оценки параметра попадает в область 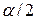, то гипотеза отвергается, если нет, то гипотеза принимается с надежностью .

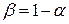Данный подход широко используется при оценке качества продукции. Так если по выборке из партии оценка результата попадает в интервал 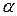, то партия бракуется. Уровень значимости назначают от 1% до 10%, то есть от величины a зависит величина заслона некачественной продукции. Не случайно для продукции, которая выпускается на экспорт уровень значимости a – очень велик. Если уровень значимости a низкий, то вероятность пропустить некачественную продукцию увеличивается.

Однако, при оценке продукции можно забраковать хорошую партию изделий из-за некачественной выборки. Это и есть ошибка второго рода.

Ошибка второго рода рассматривается, когда вводится конкурирующая гипотеза.

	– табличное

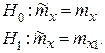
Графически гипотезы представим на рисунке 2.4

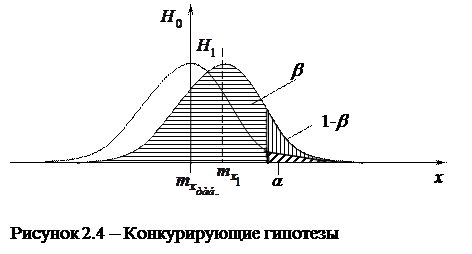
На рисунке 2.4 мы видим, что a – это риск поставщика, вероятность забраковать качественную продукцию (отвергнуть гипотезу Н₀).

b – это риск заказчика, вероятность принятия неверной гипотезы.

1 – b – вероятность отвергнуть неверную гипотезу (функция мощности критерия).

Если a уменьшать, то b будет увеличиваться, то есть если риск поставщика уменьшить, то риск заказчика будет увеличиваться.

Функция мощности критерия в зависимости от b приведена в таблице 2.3.

Таблица 2.3 – Функция мощности критерия

a	1 %	2,5 %	5 %	10 %
1 – b	0,627	0,728	0,800	0,867
b	0,373	0,272	0,200	0,133

Мощность критерия подчиняется статистике :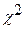

.

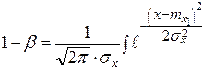Итак, допустим, полученное математическое ожидание m_x1 отличается от табличного значения. Приняли гипотезу в виде закона распределения случайной величины m_x1. Значения a и b назначили. Необходимо определить количество опытов, чтобы удовлетворить заданным a и b.

Имея уровень доверительной вероятности a для нормального закона, запишем:

;

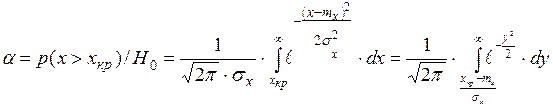– для гипотезы :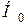

;

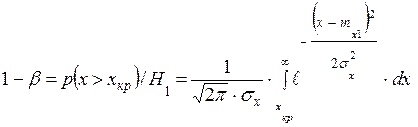– для новой гипотезы H ₁:

y_кр^a=(х_кр-m_х)/s_х ,

где m_x – табличное значение.

y_кр^1-b=(х_кр-m_х1)/s_х ,

где m_x1 – конкурирующее значение.

Произведем замену переменных ,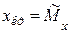

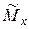– случайная величина (оценка), имеет отклонение

,

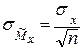тогда

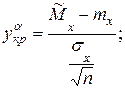
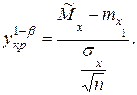
Дата добавления: 2014-11-29