
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервальная оценка параметров
|
|
|
|
Экспериментальных данных
Статистические методы анализа и обработки
2.1.1 Приближенные методы построения доверительных интервалов
В ряде задач требуется не только найти для параметра 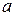 подходящее численное значение, но и оценить его точность и надежность. Требуется знать – к каким ошибкам может привести замена неизвестного параметра
подходящее численное значение, но и оценить его точность и надежность. Требуется знать – к каким ошибкам может привести замена неизвестного параметра 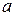 его точечной оценкой
его точечной оценкой 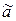 (точечная оценка - оценка, которая определяется одним числом) и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы.
(точечная оценка - оценка, которая определяется одним числом) и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы.
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 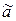 в значительной мере случайна и приближенная замена
в значительной мере случайна и приближенная замена 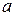 на
на 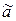 может привести к серьезным ошибкам.
может привести к серьезным ошибкам.
Чтобы дать представление о точности и надежности оценки 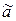 , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Все оценки параметров распределения выборки носят случайный характер и от параметров генеральной совокупности могут сильно отличаться. Нас интересует интервал  J
J 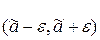 , который с заданной надежностью
, который с заданной надежностью 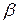
 накрывал бы неслучайное значение параметра генеральной совокупности
накрывал бы неслучайное значение параметра генеральной совокупности 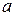 , такой интервал называется доверительным. Понятия надежность и доверительная вероятность равнозначны. Обычно величину доверительной вероятности принимают в пределах от 0.95 до 0.99.
, такой интервал называется доверительным. Понятия надежность и доверительная вероятность равнозначны. Обычно величину доверительной вероятности принимают в пределах от 0.95 до 0.99.
Нахождение доверительных интервалов основано на том, что математическое ожидание, дисперсия и сама оценка распределена по нормальному закону. Как при заданной надежности  (доверительной вероятности) найти интервал
(доверительной вероятности) найти интервал  J
J 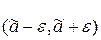 , чтобы этим интервалом накрыть оценку параметра
, чтобы этим интервалом накрыть оценку параметра 
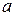 ? В данном случае
? В данном случае 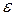 – выступает как мера точности. Приближенный метод нахождения интервала заключается в том, что в выражении для
– выступает как мера точности. Приближенный метод нахождения интервала заключается в том, что в выражении для 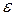 неизвестные параметры заменяют их точечными оценками. При сравнительно большом числе опытов n (порядка 20-30) этот прием обычно дает удовлетворительные по точности результаты.
неизвестные параметры заменяют их точечными оценками. При сравнительно большом числе опытов n (порядка 20-30) этот прием обычно дает удовлетворительные по точности результаты.
Вероятность того, что оценка не превысит интервал 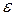 – подчиняется нормальному закону:
– подчиняется нормальному закону:
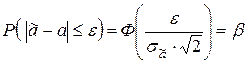 ,
,
отсюда получим следующее выражение:
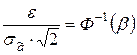 ,
,
где 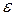 – точность оценки;
– точность оценки;
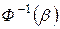 – функция Лапласа.
– функция Лапласа.
Это выражение позволит рассчитать точность оценки
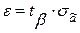 ,
,
где  – среднеквадратичное отклонение оценки параметра
– среднеквадратичное отклонение оценки параметра 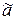 ;
;
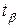 – распределение Лапласа (определяется в зависимости от величины доверительной вероятности
– распределение Лапласа (определяется в зависимости от величины доверительной вероятности 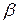 (таблица 2.1)).
(таблица 2.1)).
Таблица 2.1 – Распределение Лапласа 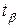
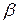
| 0,9 | 0,95 | 0,975 | 0,99 |
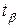
| 1,643 | 1,960 | 2,247 | 2,576 |
В качестве примера рассмотрим задачу о доверительном интервале для математического ожидания.
Точность оценки определим по формуле:
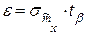 ,
,
с другой стороны среднеквадратическое отклонение оценки математического ожидания равно
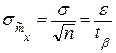 ,
,
отсюда получим количество опытов
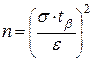 .
.
Пример №1. В результате равноточных измерений получили ошибку измерения 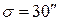 , а
, а 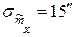 . Сколько необходимо произвести опытов, чтобы обеспечить заданную точность и надежность?
. Сколько необходимо произвести опытов, чтобы обеспечить заданную точность и надежность?
Зададим величину доверительной вероятности 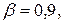 тогда
тогда 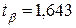 .
.
Если выбрать доверительный интервал 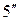 секунд, то по формуле получим:
секунд, то по формуле получим:
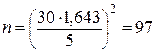 опытов.
опытов.
Если выбрать доверительный интервал 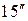 секунд, то по формуле получим:
секунд, то по формуле получим:
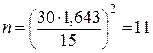 опытов.
опытов.
Вывод: С увеличением доверительного интервала, количество опытов уменьшается, чтобы интервалом накрыть нашу оценку.
Пример № 2. Построить доверительный интервал J 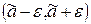 при доверительной вероятности
при доверительной вероятности 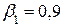 и
и 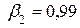 , если
, если 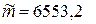 м, а
м, а 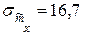 м.
м.
Из таблицы 2.1
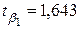 и
и 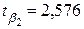 ;
; 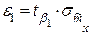 ;
; 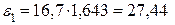 м;
м; 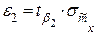 ;
; 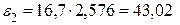 м;
м;
J 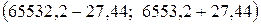 , J
, J 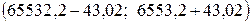 .
.
2.1.2 Точные методы построения доверительных интервалов
(применительно к математическому ожиданию и дисперсии)
До сих пор при определении доверительных интервалов пользовались статистикой нормального закона распределения.
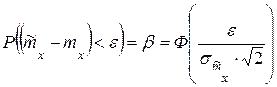 .
.
Нормальный закон дает хорошие результаты при большом количестве выборки n. При малом количестве выборки n лучше пользоваться статистикой Стьюдента.
Формула Стьюдента очень сложная и имеет вид:
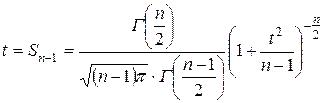 ,
,
где 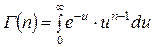 – Гамма функция.
– Гамма функция.
Для удобства работы с функцией Стьюдента вводится новая переменная
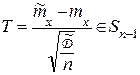 ,
,
где 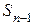 – распределение по закону Стьюдента (представленное в виде таблицы приложения Г);
– распределение по закону Стьюдента (представленное в виде таблицы приложения Г);
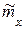 – оценка математического ожидания;
– оценка математического ожидания;
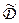 – оценка дисперсии распределения.
– оценка дисперсии распределения.
Тогда в новых переменных функцию распределения запишем в виде:
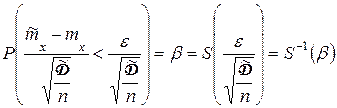 ,
,
отсюда
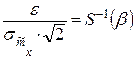 ,
,
и ошибка будет равна
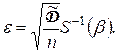
Точный метод основан на использовании закона распределения Стьюдента.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1327; Нарушение авторских прав?; Мы поможем в написании вашей работы!