Приближенный способ формирования случайной величины с произвольной функцией распределения

Случайная величина может быть задана дискретно. В этом случае интеграл от закона распределения не берется.

1 Способ формирования случайной дискретной величины.

Предположим, что случайная величина принимает следующие значения

.

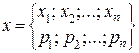Условие нормировки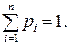

Для реализации дискретного распределения берется отрезок единичной длины и разбивается на интервалы

Длина отрезков пропорциональна вероятности. Тогда вероятность того, что случайная величина примет случайное значение от 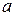до

,

при условии, что внутри каждого интервала плотность распределения равна единице.

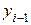Вероятность того, что примет значение до 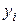будет равно

,

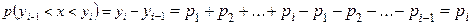то есть, равна длине интервала 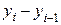или вероятности.

Формулируем случайную величину R, равномерно распределенную на интервале 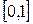. Определяем в какой интервал попадет R, затем по интервалу определяем вероятность и присваиваем ей значение, которое определено исходными данными (рисунок 1.5).

Рисунок 1.5 – Распределение вероятностей на интервале

Все точки в интервале p₁будут принимать значение 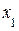. Таким образом, можно формировать любое дискретное распределение.

2 Способ формирования случайной величины , заданной непрерывной функцией.

Допустим, непрерывная функция распределения может быть получена опытным путем, а аналитически описать ее не представляется возможным или результат описания опытного распределения не удовлетворяет исследователя. В этом случае используют данный способ.

На первом этапе определяем интервал изменения случайной величины от 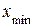до 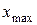. Весь интервал изменения случайной величины делится на n равных интервалов 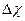(рисунок 1.6)

.

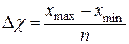Рисунок 1.6 – Произвольный закон распределения

На каждом интервале строим криволинейную трапецию, основание которой является , а верхняя часть кривая функции. В виду того, что 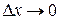, тогда площадь криволинейной i -ой трапеции определяется выражением:

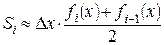. (1.22)

На каждом интервале строим прямоугольник, площадь которого эквивалентна площади элементарной криволинейной трапеции. Высота прямоугольника равна

.

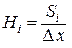Теперь необходимо нормировать всю площадь под кривой из условия, что

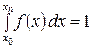. (1.23)

Сумма всех площадей

.

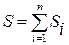Нормализацию проводим по зависимости

,

тогда, если сложить

.

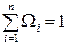Единичный интервал [0,1] разбиваем на интервалы, соответствующие нормированным площадям . Вероятность того, что случайная величина попадет в интервал .

Внутри каждого интервала случайная величина будет распределена равномерно при условии, что .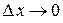

Формирование случайной величины по заданному закону производится следующим образом:

1 Генерируется случайная величина R, определяется интервал i, в котором приобретает значение формируемая случайная величина.

2 Производится вторичное генерирование случайной величины R. Учитывая, что внутри каждого интервала случайная величина распределена равномерно, то по формуле равновероятного распределения получим

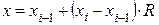. (1.24)

Дата добавления: 2014-11-29