
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределения
|
|
|
|
Формирование случайных величин с заданными законами
Существуют различные способы «порождать» случайные числа с помощью ЭВМ.
Например, метод обратных функций, метод суперпозиции.
Важно понять, что для получения значений случайных величин с произвольной функцией распределения достаточно уметь находить значения какой-нибудь одной «стандартной» случайной величины, так как всегда можно подобрать такую функцию от этой случайной величины, которая имела бы требуемый закон распределения. В качестве такой случайной величины обычно берут случайную величину R, имеющую равномерное распределение на отрезке 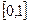 . Формирование случайных величин с заданным законом распределения будем осуществлять методом обратного преобразования. Сформулируем правила метода обратных функций.
. Формирование случайных величин с заданным законом распределения будем осуществлять методом обратного преобразования. Сформулируем правила метода обратных функций.
Правило 1. Для того чтобы разыграть возможное значение xi непрерывной случайной величины Х, зная ее функцию распределения F(x), надо выбрать случайное число ri, приравнять его функции распределения и решить относительно xi полученное уравнение F(xi)=ri.
Если известна плотность вероятности f(x), то используют правило 2.
Правило 2. Для того чтобы разыграть возможное значение xi непрерывной случайной величины Х, зная ее плотность вероятности f(x), надо выбрать случайное число ri и решить относительно xi уравнение
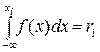 ,
,
или уравнение
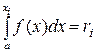 ,
,
где α – наименьшее конечное возможное значение Х.
Рассмотрим более подробно данный метод. Необходимо сформировать случайную величину Х, для которой задана функция распределения:
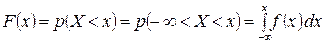 . (1.4)
. (1.4)
Интегральная функция 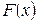 изменяется от 0 до 1. Приравняв функцию
изменяется от 0 до 1. Приравняв функцию 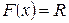 можно путем обратного преобразования построить величину
можно путем обратного преобразования построить величину 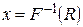 , которая будет соответствовать заданной функции. Построим график обратного преобразования для равномерного закона распределения (рисунок 1.2).
, которая будет соответствовать заданной функции. Построим график обратного преобразования для равномерного закона распределения (рисунок 1.2).
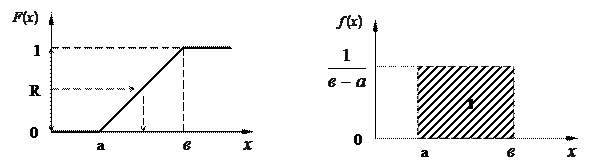
Рисунок 1.2 – Обратное преобразование
Формируем случайную величину R в интервале от 0 до 1 и путем обратного преобразования оказываемся в интервале 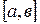 .
.
Определим аналитические выражения для осуществления обратного преобразования.
1 Формирование случайного числа по равномерному закону.
Плотность распределения для равномерного закона имеет вид:
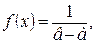 (1.5)
(1.5)
где  – принимает любое значение от
– принимает любое значение от 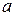 до
до  .
.
Запишем интегральный закон распределения:
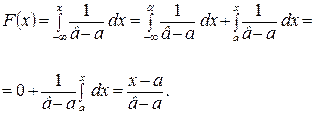 (1.6)
(1.6)
Приравниваем F(x) значению R и, решая уравнение относительно  , получим
, получим
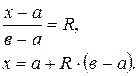 (1.7)
(1.7)
В выражении (1.7) величина  равномерно распределена в интервале от
равномерно распределена в интервале от 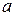 до
до  в соответствии с заданной функцией (1.5).
в соответствии с заданной функцией (1.5).
2 Формирование случайного числа по экспоненциальному закону.
Плотность распределения для экспоненциального закона имеет вид (рисунок 1.3)
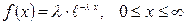 . (1.8)
. (1.8)
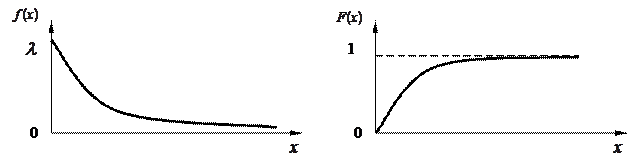
Рисунок 1.3 – Экспоненциальный закон распределения
Интегральная функция
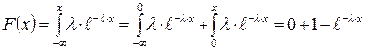 . (1.9)
. (1.9)
Приравниваем полученное выражение R и решим полученное уравнение относительно  .
.
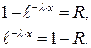 (1.10)
(1.10)
Логарифмируем левую и правую часть, получаем выражение
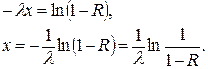 (1.11)
(1.11)
Если сформировать случайное число R и по формуле (1.11) определить  , тогда вычисленное значение будет распределено по экспоненциальному закону с заданной интенсивностью
, тогда вычисленное значение будет распределено по экспоненциальному закону с заданной интенсивностью 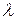 .
.
3 Формирование случайного числа по нормальному закону.
Согласно центральной предельной теореме Ляпунова закон распределения суммы m независимых случайных величин, имеющих один и тот же произвольный закон распределения при необратимом увеличении числа слагаемых m, приближается к нормальному закону.
При сумме двух равномерно распределенных случайных величин в интервале 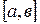 получаем треугольное распределение в интервале
получаем треугольное распределение в интервале 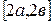 . При сумме трех случайно распределенных величин в интервале
. При сумме трех случайно распределенных величин в интервале 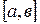 получаем распределение в интервале
получаем распределение в интервале 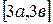 , которое приближается к нормальному закону распределения (рисунок 1.4).
, которое приближается к нормальному закону распределения (рисунок 1.4).
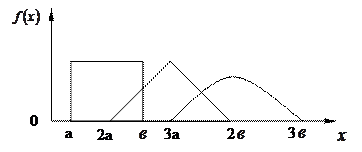
Рисунок 1.4 – Композиция случайных величин
Сумма m равномерно распределенных в интервале от 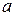 до
до  независимых случайных величин стремится к нормальному распределению.
независимых случайных величин стремится к нормальному распределению.
Математическое ожидание и дисперсия для суммы равномерных законов на интервале 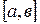 имеет вид:
имеет вид:
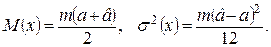 (1.12)
(1.12)
Если выбрать интервал 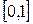 , то математическое ожидание и дисперсия будут оцениваться по зависимостям:
, то математическое ожидание и дисперсия будут оцениваться по зависимостям:
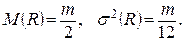 (1.13)
(1.13)
Для получения последовательности нормально распределенных случайных величин с заданными 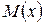 и D (
и D ( ) мы должны использовать величину Zi, которая будет являться нормально распределенной случайной величиной, с параметрами N(0,1). Тогда случайная величина
) мы должны использовать величину Zi, которая будет являться нормально распределенной случайной величиной, с параметрами N(0,1). Тогда случайная величина 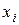 будет определяться по формуле:
будет определяться по формуле:
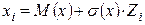 .
.
Пусть 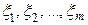 – независимые случайные величины, равномерно-распределенные на отрезке
– независимые случайные величины, равномерно-распределенные на отрезке 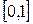 , с
, с 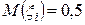 ;
; 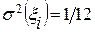 . Просуммируем независимые случайные величины:
. Просуммируем независимые случайные величины:
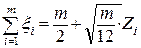 , (1.14)
, (1.14)
отсюда нормированная величина будет иметь вид:
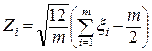 , (1.15)
, (1.15)
где m – количество реализаций.
При 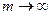 случайная величина Zi стремится к стандартной нормально распределенной случайной величине с нулевым математическим ожиданием и дисперсией равной 1.
случайная величина Zi стремится к стандартной нормально распределенной случайной величине с нулевым математическим ожиданием и дисперсией равной 1.
На практике обычно берут m = 12, поэтому:
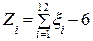 . (1.16)
. (1.16)
Таким образом, моделирование случайной величины 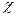 =N(
=N(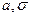 ), имеющее нормальное распределение с параметрами
), имеющее нормальное распределение с параметрами 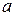 и
и 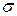 , основано на использовании зависимости:
, основано на использовании зависимости:
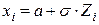 , (1.17)
, (1.17)

где Zi = N(0,1).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 728; Нарушение авторских прав?; Мы поможем в написании вашей работы!