
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема про середнє значення визначеного інтеграла
|
|
|
|
Теорема 1. Якщо функція f(x) інтегрована на відрізку [a; b], то справджуються нерівності
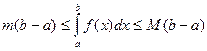 (11)
(11)
де М і m – деякі числа.
Д о в е д е н н я. Оскільки функція f(x) інтегрована, на відрізку [a; b], то вона обмежена на цьому відрізку, тобто існують такі числа М і m, що
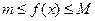 , x є [a; b],
, x є [a; b],
Користуючись властивістю визначеного інтеграла, маємо
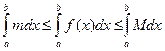
Підставляючи в ці нерівності значення інтегралів,
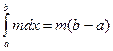
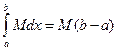
дістанемо нерівність (11). Зауважимо, що нерівності (11) можна записати у вигляді рівності. Для цього члени нерівностей (11) поділимо на число b-a і введемо позначення
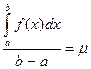
Тоді матимемо таку рівність:
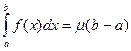
де m≤µ≤M.
Н а с л і д о к. Якщо функція f(x) неперервна на відрізку [a; b], то існує точка с 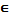 [a; b] така, що виконується рівність
[a; b] така, що виконується рівність
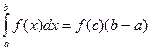 (12)
(12)
Справді, за теоремою Вейєрштрасса неперервна на відрізку [a; b] функція набуває свого найменшого і найбільшого значень, відповідно m і М. Тоді за теоремою про проміжне значення неперервної функції існує хоча б одна точка с 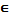 [a; b], в якій функція дорівнює числу µ.
[a; b], в якій функція дорівнює числу µ.
Цей наслідок називають ще т е о р е м о ю п р о с е р е д н є
з н а ч е н н я в и з н а ч е н о г о і н т е г р а л а від неперервної функції.
З’ясуємо геометричний зміст цієї теореми. Припустимо, що функція f(x)>0 і неперервна на відрізку [a; b]. Тоді інтеграл 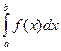 виражає площу криволінійної трапеції (рис. 48). Добуток f(c)(b-a) є площа прямокутника з основою b-a і висотою f(c).
виражає площу криволінійної трапеції (рис. 48). Добуток f(c)(b-a) є площа прямокутника з основою b-a і висотою f(c).
Отже, згідно з рівністю (12), на кривій, яка є графіком функції f(x), знайдеться хоча б одна точка М така, що площа криволінійної трапеції дорівнює площі прямокутника з тією самою основою, а висота його дорівнює ординаті точки М. У цьому полягає геометричний зміст теореми про середнє для неперервної функції.
Т е о р е м а 2. Нехай функції f(x) i g(x) визначені і неперервні на відрізку
[a; b], причому g(x) на відрузку [a; b] не змінює знака, g(x)≥0 або g(x)≤0.
Тоді існує таке число с 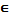 [a; b], що
[a; b], що
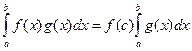 (13)
(13)
Д о в е д е н н я. Нехай g(x) набуває на відрізку [a; b] невід’ємних значень. Тоді
mg(x)≤f(x)g(x)≤Mg(x),
Де m, М – відповідно найменше і найбільше значення функції f(x) на відрізку
[a; b]. Функція f(x) g(x) неперервна на відрізку [a; b], отже, вона інтегрована на цьому відрізку. Тоді маємо
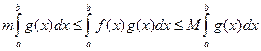
Якщо 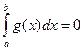 , то рівність (13) справджується, бо тоді
, то рівність (13) справджується, бо тоді
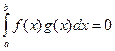 . Отже, рівність (13) справедлива при будь-якому f(c). Теорему доведено.
. Отже, рівність (13) справедлива при будь-якому f(c). Теорему доведено.
Якщо 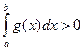 , то поділивши всі члени попередньої нерівності на
, то поділивши всі члени попередньої нерівності на 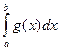 , дістанемо
, дістанемо
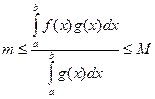
Введемо позначення
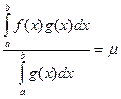
Тоді
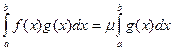
де m≤µ≤M. Оскільки f(x) є неперервною на відрізку [a; b], то
iснує така точка с 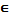 (a; b), що f(c)=µ. Теорему доведено.
(a; b), що f(c)=µ. Теорему доведено.
Зауважимо, що теорема 1 є окремим випадком теореми 2. Справді, припустивши в теоремі 2, що g(x)=1, матимемо теорему 1.
Назва теореми 1 як інтегральної теореми про середнє пояснюється тим, що в даному разі стверджується існування деякої точки, яка міститься всередині відрізка і має певну властивість, пов’язану з визначеним інтегралом функції.
Теорему 2 називають у з а г а л ь н е н о ю т е о р е м о ю п р о
с е р е д н є.
Ми розглянули випадок, коли a<b. Теореми 1,2 залишаються справедливими й тоді, коли a>b.
Наприкінці зауважимо, що число
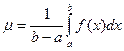 (14)
(14)
називають с е р е д н і м з н а ч е н н я м ф у н к ц і ї f(x) на відрізку [a; b].
ПРИКЛАД
Знайти середнє значення функції 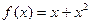 на відрізку [0; 2].
на відрізку [0; 2].
Р о з в’ я з а н н я. Застосуємо формулу (14). Для цього обчислимо інтеграл
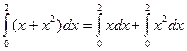 (15)
(15)
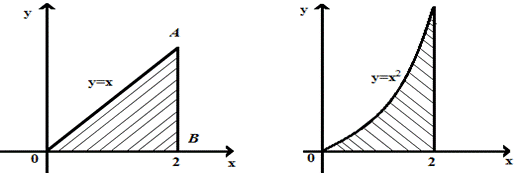
Перший інтеграл в правій частині рівності (15) вражає площу трикутника ОАВ (рис. 49), а другий – площу під параболою (рис. 50). Отже,
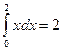 ,
, 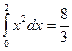
Тоді 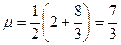
Лекція 25
Матеріал для самостійного опрацювання
Основні властивості визначеного інтеграла
Будемо вважати, що всі функції на проміжках інтегрування є інтегралами.
10. Значення визначеного інтеграла не залежить від значення змінної інтегрування.
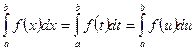 (1)
(1)
Це випливає з означення інтегралу як числа, що дорівнює границі інтегральних сум.
20. 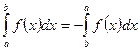 (2)
(2)
30.
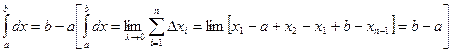 (3)
(3)
40.
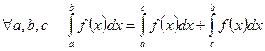 (4)
(4)
Нехай a<c<b. Так як границя інтегральної суми не залежить від способу розбиття відрізка [а;b], то будимо проводити розбиття так, щоб точка с завжди була точкою розбиття. Якщо c=xm, то
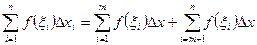
Перейшовши до границі при 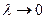 одержуємо (4).
одержуємо (4).
Нехай тепер a<b<c. Застосуємо до відрізка [а;с] тільки що доведене співвідношення
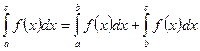
Враховуючи те, що
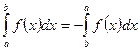
маємо
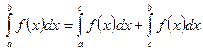
Для іншого розташування точок a,b,c доведення те ж саме.
50.
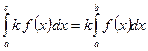
Дійсно, для будь-якого розбиття проміжку [а;b] і будь-якого вибору точок 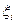
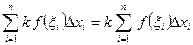
Переходячи до границі маємо

60. 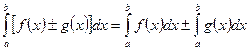
Доведення. Так як будь-яке розбиття відрізка [а;b] і 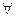 вибору точок
вибору точок 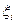
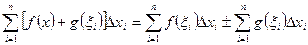
то 
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 12403; Нарушение авторских прав?; Мы поможем в написании вашей работы!