Безынерционное звено

Типовые динамические звенья

Понятием типовое звено в теорию введен еще один исключительно удобный расчетно-аналитический инструмент. Из всего многообразия возможных динамических звеньев выделена группа простейших, но таких, из которых может быть собрана модель системы любой сложности. Для типовых звеньев введены следующие правила и ограничения: 1) порядок дифференциального уравнения должен быть не выше второй степени; 2) в уравнении звена слева от знака равенства ставится выходная переменная и ее производные, справа - входная переменная и ее производные; 3) уравнение звена «нормализуется» тем, что коэффициент при выходной переменной приводится к единице.

Уравнение любого типового звена получается из дифференциального уравнения второго порядка выбором его отдельных слагаемых

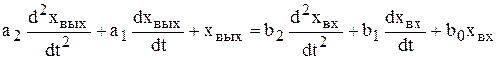. (4.12)

Ниже рассмотрены свойства и характеристики основных типовых звеньев, при этом их уравнения записаны для неединичных входных воздействий.

Уравнение динамики этого звена описывается алгебраическим уравнением

,(4.13)

где k– коэффициент передачи (усиления) звена.

Операторное уравнение звена и его передаточные функции имеют вид

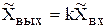, (4.14)

,

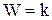. (4.15)

Переходная характеристика звена определяется уравнением (4.13) и показывает, что при передаче через звено форма воздействия не меняется, а изменяется лишь его масштаб. Например, при подаче на вход ступенчатого воздействия, выходное воздействие устанавливается мгновенно, изменяясь в k раз (рис. 4.4,а).

Примеры. Безынерционными звеньями могут служить потенциометр (как делитель напряжения), жесткий рычаг, механический редуктор и другие, если уравнения их динамики можно представить уравнением вида (4.13).

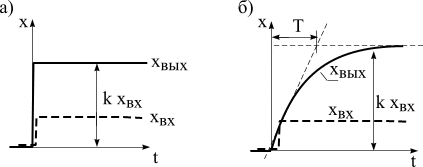Рис. 4.4. Переходные функции звеньев:

а) безынерционного, б) апериодического первого порядка

Дата добавления: 2014-11-29