Дифференцирующие звенья

Дифференцирующие звенья реагируют на скорость изменения входного воздействия, и поэтому в их дифференциальных уравнениях в правой части содержатся производные от входной переменной.

Идеальное дифференцирующее звено. Уравнение динамики звена, его операторное уравнение и передаточная функция имеют вид:

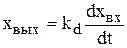(4.40)

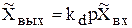(4.41)

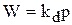. (4.42)

Переходная характеристика звена представляет собой импульс с бесконечной амплитудой и бесконечно малой шириной (рис. 4.9,а) и записывается уравнением

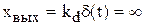. (4.43)

Действительно, идеальных дифференцирующих звеньев в природе нет, так как любое устройство обладает некоторой инерционностью и потерями, но некоторые технические устройства при определенных допущениях могут представляться таким звеном (см. пример 4.5).

Реальное дифференцирующее звено без статизма. Учет инерционности дает следующее уравнение динамики

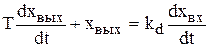. (4.44)

Передаточная функция и переходная характеристика звена запишутся следующим образом

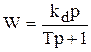, (4.45)

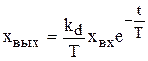. (4.46)

График переходной характеристики звена показан на рис. 4.9,б.

Реальное дифференцирующее звено со статизмом. Уравнение звена

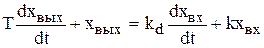. (4.47)

Передаточная функция и переходная характеристика звена запишутся так

, (4.48)

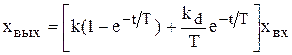. (4.49)

График переходной характеристики звена показан на рис. 4.9,в.

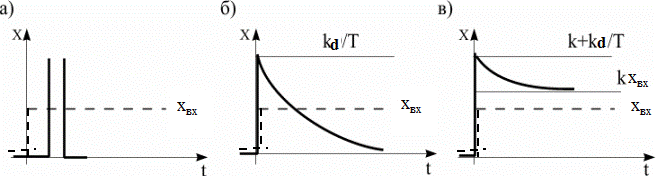
Рис. 4.9. Переходные характеристики дифференцирующих звеньев:

а) идеальное, б) реальное без статизма, в) реальное со статизмом

Пример 4.5. Близким к идеальному дифференцирующему звену можно считать тахогенератор постоянного тока (рис. 4.10,а), если входом считать угол поворота ротора 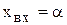, а выходом его напряжение .

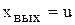Действительно, при постоянном потоке возбуждения э.д.с. будет пропорциональна частоте вращения 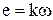и так как 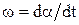, то для режима холостого хода получим

.

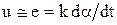Пример 4.6. Реальным звеном без статизма является С-Rконтур (рис. 4.10,б), если принять 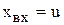, 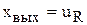. Из уравнения баланса напряжений

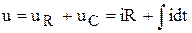
после однократного дифференцирования и простых преобразований получим

,

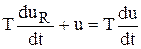где Т=RC - постоянная времени.

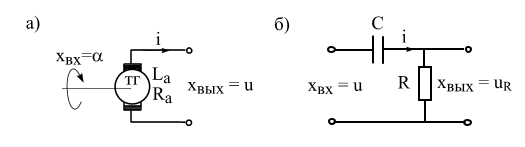Рис. 4.10. Примеры дифференцирующих звеньев

Дата добавления: 2014-11-29