Инерционное звено второго порядка

Уравнение динамики звена

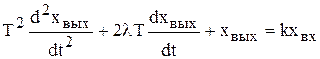, (4.20)

где Т –постоянная времени, 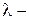коэффициент демпфирования, 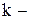коэффициент передачи звена.

Операторное уравнение и передаточная функция звена следующие:

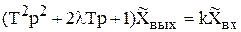, (4.21)

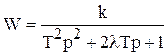. (4.22)

Отличительной чертой этого звена является возможность существования трех видов переходных характеристик, что определяется корнями его характеристического уравнения 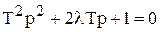. Корни этого уравнения

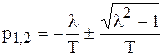(4.23)

могут быть вещественными, комплексными или чисто мнимыми, определяя в каждом случае свой переходный процесс. При этом обычно говорят о трех типах звеньев.

Апериодическое звено второго порядка. При 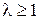корни вещественные, и переходная функция определяется формулой

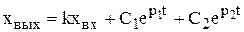. (4.24)

Переходный процесс имеет апериодический характер, протекающий без колебаний (рис. 4.6,а). Можно показать, что в этом режиме звено эквивалентно последовательному соединению двух апериодических звеньев первого порядка с постоянными времени T₁, T₂ и коэффициентами передачи k₁, k₂ . Поэтому передаточная функция звена может быть записана также в виде

.

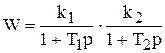Колебательное звено. При l<1 корни характеристического уравнения комплексные

,

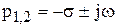где 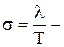коэффициент затухания, а 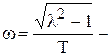угловая частота свободных колебаний. Переходная характеристика колебательного звена определяется уравнением

,

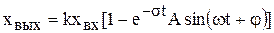где 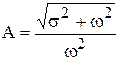и 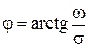- соответственно амплитуда, и фаза свободных колебаний. Переходный процесс показан на рис. 4.6,б.

Консервативное звено. При 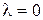корни становятся чисто мнимыми

, (4.27)

и звено представляет собой идеализированный случай звена без потерь. Переходный процесс носит незатухающий колебательный характер (рис.4.6, в).

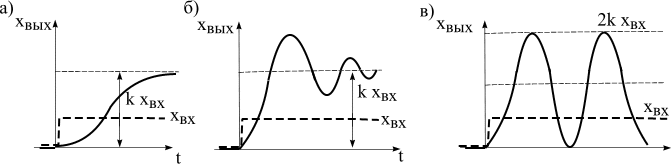Рис. 4.6. Переходные функции инерционных звеньев второго порядка

Примеры. К инерционным звеньям второго порядка относятся элементы, способные запасать потенциальную и кинетическую энергию и преобразовывать их одну в другую. Такими возможностями обладают: электрические R-L-С контуры; электромеханические устройства, например, двигатели, у которых кинетическая энергия запасается в якоре, а электромагнитная (потенциальная) в якорной цепи; механические элементы, обладающие массой, упругостью и вязким трением и т. д.

Пример 4.2. Для R-L-Cконтура справедливо уравнение

.

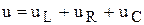Используя известные формулы: 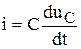, , 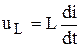, 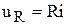получим

.

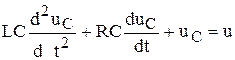Это уравнение инерционного звена второго порядка, в котором , .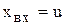

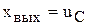Дата добавления: 2014-11-29