
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамические характеристики звена
|
|
|
|
Автоматические системы относятся к классу динамических систем, потому что процессы регулирования, протекающие в них, сопровождаются постоянными изменениями во времени. Математическое описание этих систем построено в основном на дифференциальных и алгебраических уравнениях. Динамическое звено, как элементарный компонент математической модели системы, также обладает динамическими свойствами и описывается своим уравнением.
Дифференциальное уравнение звена. Это уравнение определяет временную зависимость выходной величины звена от входной величины
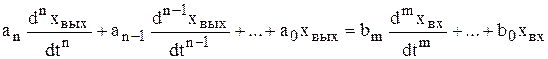 . (4.1)
. (4.1)
Преобразование Лапласа для этого уравнения дает операторную форму
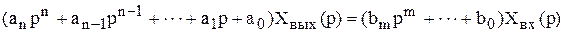 . (4.2)
. (4.2)
или сокращенно
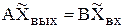
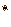 (4.3)
(4.3)
Так как свободное движение звена происходит при отсутствии сигнала на его входе, то это состояние описывается однородным дифференциальным уравнением
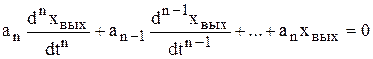 , (4.4)
, (4.4)
по которому определяется характеристическое уравнение звена
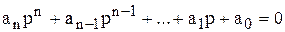 . (4.5)
. (4.5)
Корни характеристического уравнения  определяют динамические свойства звена и их значения являются предметом особого внимания, как при проектировании, так и при эксплуатации автоматических систем.
определяют динамические свойства звена и их значения являются предметом особого внимания, как при проектировании, так и при эксплуатации автоматических систем.
Характер переходного процесса в звене определяется двумя факторами: внутренними свойствами звена, которые описываются уравнением (4.4), и формой входного воздействия, которое учитывается в правой части уравнения (4.1).
Типовые входные воздействия. Для того, чтобы иметь возможность классифицировать динамические звенья, используют типовые входные воздействия. Набор этих воздействий подобран таким образом, чтобы получить исчерпывающий динамический портрет звена.
Ступенчатое воздействие (рис. 4.2,а) представляет скачкообразное изменение сигнала во времени. В теории и практике расчетов используются как единичные*, так и неединичные воздействия. Единичное воздействие обозначают 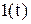 . Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена. Неединичное воздействие обозначают
. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена. Неединичное воздействие обозначают  .
.
Примерами ступенчатых воздействий можно считать мгновенное замыкание или размыкание электрической цепи постоянного тока, внезапное приложение или сброс нагрузки (например, момента в системах поддержания заданной скорости двигателя) и т. д. Ступенчатое воздействие используется для получения переходной функции звена.
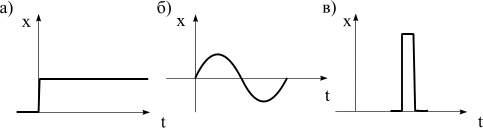 |
Рис. 4.2
______________________________________
* В дальнейшем функции от переменной “p” будем обозначать волнистой линией, например, вместо 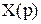 будем писать будем писать  . .
|
Гармоническое воздействие (рис. 4.2,б) представляет синусоидальный во времени сигнал и используется при анализе частотных свойств звена.
Единичное импульсное воздействие (рис. 4.2,в) представляет импульс прямоугольной или другой формы, за время существования которого реакция системы остается практически постоянной. Если устремить ширину импульса к нулю, оставляя при этом неизменной его площадь, то в пределе получается единичный импульс, называемый d-импульсом. Понятие d-импульса применяется для получения импульсных характеристик звена.
Описание динамических свойств звена производится в виде следующих специальных функций и характеристик: переходная функция, передаточная функция, частотная передаточная функция, частотные характеристики звена, логарифмические частотные характеристики (ЛЧХ).
Переходная функция. Эта функция представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход ступенчатого воздействия. При единичном входном воздействии переходную функцию обозначают 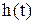 , а при неединичном
, а при неединичном 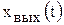 . Переходная функция получается либо в результате решения дифференциального уравнения звена, либо экспериментально.
. Переходная функция получается либо в результате решения дифференциального уравнения звена, либо экспериментально.
____________________________________________________________________
Комментарий к понятию “единичное воздействие”. Работа с единичными воздействиями позволяет через единичный сигнал выразить непрерывные сигналы любой формы. Например, если на входе системы действует сигнал f(t) рис.4.3, то его можно представить либо в виде суммы скачков 1,2,3,... определенных интенсивностей, подаваемых в определенные моменты времени 0,t1, t2,... (рис.4.3, а), либо через суммы импульсов подаваемых в равные промежутки времени (рис.4.3, б). Найдя реакцию системы на каждый скачок (импульс) и просуммировав результат, получим реакцию системы на сложный входной сигнал f(t).
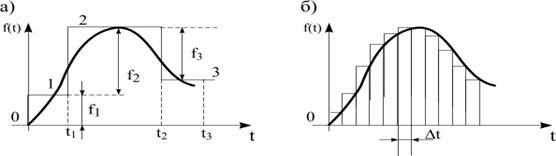 Рис. 4.3
Рис. 4.3
|
Передаточная функция. Представляет собой отношение операторных значений выходного воздействия к входному воздействию
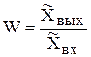 . (4.6)
. (4.6)
Из уравнения (4.3) следует также, что

и это показывает, что знаменателем передаточной функции звена всегда является его характеристическое уравнение.
Несмотря на то, что передаточная функция это просто другая форма записи операторного уравнения звена, форма настолько эффективна, что стала одним из главных математических инструментов теории автоматического управления.
Частотная передаточная функция и частотные характеристики звена. Каждое звено можно рассматривать как устройство с присущими ему определенными частотными свойствами, которые отображают его динамические свойства. Частотная передаточная функция это реакция звена на входное гармоническое воздействие.
Если звено линейное и на его входе действует синусоидальное воздействие
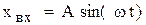 ,
,
то на выходе звена воздействие будет отличаться только амплитудой и фазой
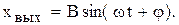
(Как известно, в линейных физических элементах частота сигнала не изменяется.) Так как при работе с синусоидальными функциями предпочтительной является комплексная форма записи, то, пользуясь формулой Эйлера,
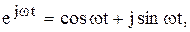
пишут
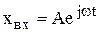 ,
, 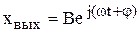
подразумевая при этом, что используется только мнимая часть 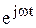 .
.
Если амплитуду входного сигнала “А” оставлять неизменной, но изменять частоту  , то каждой частоте будет соответствовать свое значение амплитуды
, то каждой частоте будет соответствовать свое значение амплитуды 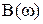 и фазы
и фазы 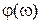 выходного сигнала. Это позволяет определить частотную передаточную функцию звена как отношение выходного сигнала к входному сигналу
выходного сигнала. Это позволяет определить частотную передаточную функцию звена как отношение выходного сигнала к входному сигналу
 (4.7)
(4.7)
Эту передаточную функцию записывают еще следующим образом
 .
.
Таким образом, наряду с понятием “частотная передаточная функция” вводятся также понятия частотных характеристик:
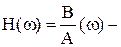 амплитудно-частотная характеристика (АЧХ);
амплитудно-частотная характеристика (АЧХ);
 фазо-частотная характеристика (ФЧХ);
фазо-частотная характеристика (ФЧХ);
 вещественная частотная характеристика;
вещественная частотная характеристика;
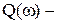 мнимая частотная характеристика.
мнимая частотная характеристика.
Покажем, что передаточные функции W(p) и W(jw) можно получать одну из другой формальной заменой оператора рна jw. Для этого запишем для синусоидальных воздействий входа и выхода следующие соотношения
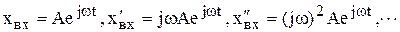



и подставим их в дифференциальное уравнение звена (4.1). После упрощений получим
 (4.8)
(4.8)
Сравнение уравнений (4.2) и (4.8) подтверждает сделанное утверждение.
Логарифмические частотные характеристики (ЛЧХ). Для построения этих характеристик используется выражение частотной передаточной функции в показательной форме
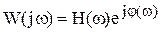 . (4.9)
. (4.9)
Логарифмируя правую и левую части уравнения (4.9), найдем
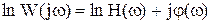 . (4.10)
. (4.10)
Выражения 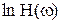 и
и 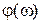 представляют соответственно логарифмическую амплитудную (ЛАХ) и логарифмическую фазовую (ЛФХ) частотные характеристики.
представляют соответственно логарифмическую амплитудную (ЛАХ) и логарифмическую фазовую (ЛФХ) частотные характеристики.
Однако в практических расчетах удобнее пользоваться десятичными логарифмами, и поэтому ЛАХ определяется в децибелах

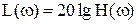 . (4.11)
. (4.11)
Примечание. Бел представляет собой логарифмическую единицу и соответствует десятикратному увеличению мощности: 1 бел - это увеличение в 10 раз, 2 бела - в 100 раз, 3 бела - в 1000 раз и т.д.. Децибел равен одной десятой части бела. Если бы 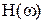 было отношением мощностей, то в формуле (4.11) стоял бы множитель 10. Но так как
было отношением мощностей, то в формуле (4.11) стоял бы множитель 10. Но так как 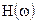 является отношением перемещений, скоростей, напряжений и т.д., то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в 100 раз, что соответствует 2 белам или 20 децибелам. Поэтому в (4.11) стоит множитель 20.
является отношением перемещений, скоростей, напряжений и т.д., то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в 100 раз, что соответствует 2 белам или 20 децибелам. Поэтому в (4.11) стоит множитель 20.
При построении логарифмических характеристик по оси абсцисс откладывается частота в логарифмическом масштабе; по оси ординат - значения амплитуд в децибелах, а углов - в градусах или радианах в равномерных масштабах.Для оценки диапазона частот при построении логарифмических характеристик используют понятия октавы и декады. Если две частоты 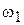 и
и  отличаются друг от друга в 2 раза, то говорят, что они отличаются на октаву
отличаются друг от друга в 2 раза, то говорят, что они отличаются на октаву
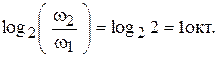
Если это отличие равно 10, то вводят понятие декады
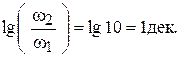
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 845; Нарушение авторских прав?; Мы поможем в написании вашей работы!