Интегрирующие звенья

Интегрирующим называется звено, в котором производится интегрирование входного воздействия, и поэтому в выходном воздействии обязательно присутствует интеграл .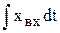

Идеальное интегрирующее звено. Уравнение динамики звена в дифференциальной и интегральной формах имеют вид

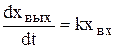, (4.28)

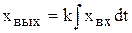. (4.29)

Операторное уравнение и передаточная функция определяются выражениями

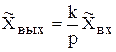, (4.30)

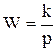. (4.31)

Переходную характеристику легко получить из уравнения (4.29), если учесть, что при ступенчатом входном сигнале 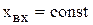и его можно вынести за знак интеграла. Это дает выражение

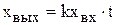. (4.32)

График переходной характеристики приведен на рис. 4.7,а.

Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением

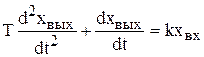, (4.33)

и имеет передаточную функцию

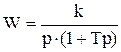. (4.34)

Отметим, что эту передаточную функцию можно записать еще так

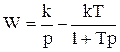, (4.35)

что позволяет представить это звено, состоящим из параллельно соединенных звеньев идеального интегрирующего звена и апериодического звена первого порядка. Как показано на рис. 4.7,б, переходная функция звена представляется суммой переходных функций двух звеньев и определяется выражением

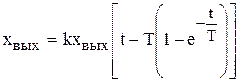. (4.36)

Изодромное звено. У равнение звена и его передаточная функция

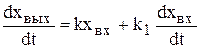(4.37)

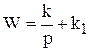. (4.38)

По виду передаточной функции можно сделать вывод, что изодромное звено составлено из параллельно включенных звеньев - идеального интегрирующего и безынерционного. Переходная функция звена определяется уравнением

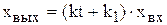(4.39)

и график ее показан на рис. 4.7, в.

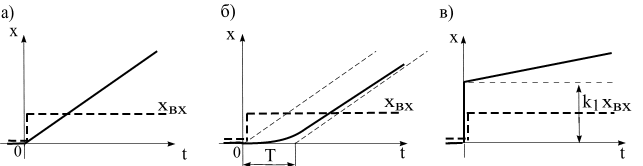Рис. 4.7. Переходные функции интегрирующих звеньев

Пример 4.3. Идеальным интегрирующим звеном можно считать двигатель постоянного тока в режиме холостого хода. Для цепи якоря справедливо уравнение

.

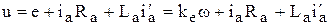Если пренебречь потерями напряжений 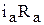, 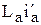и учесть, что 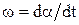, где a-угол поворота вала, получим 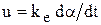. Интегрирование этого уравнения дает уравнение идеального интегрирующего звена, в котором ,

.

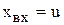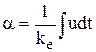Пример 4.4. Многие математические операции эффективно выполняются электронными схемами на основе операционных усилителей. Пример такой схемы дан на рис. 4.8,б.

Для этих усилителей характерно три свойства: 1) усилитель имеет исключительно большой коэффициент усиления 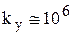; 2) ток, проходящий через усилитель настолько мал, что при составлении баланса токов им можно пренебречь; 3) потенциал в узле “а” можно принять равным нулю так как 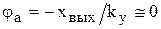, потому что 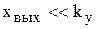. Покажем, что при данных допущениях, схема на рис. 4.8,б является идеальным интегрирующим звеном. Запишем для точки “а” уравнение баланса токов

,

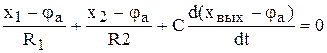принимая 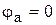и интегрируя это уравнение, получим

.

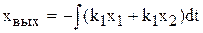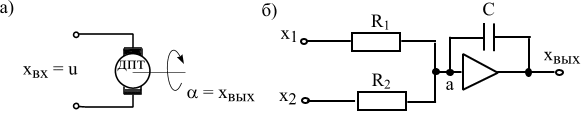Рис. 4.8. Примеры интегрирующих звеньев

Дата добавления: 2014-11-29