Функция нечетная

Функция четная

f(t)=f(-t) - функция симметрична относительно оси ординат. В этом случае при разложении отсутствуют слагаемые, содержащие синусоидальные

гармоники,т.е. О—О I (см. Выражение (1))

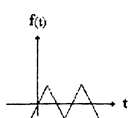
(симметрична относительно начала коордюат) f(t)= -f(-t). Отсутствуют косинусоидальные гармоники и постоянная составляющая

аn=О

З.Функция симметрична относительно оси абсцисс со

cдвигом за период

Отсутствуют гармоники с четными порядковыми номерами.

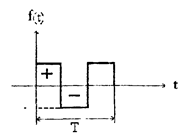
На практике могут быть комбинации рассмотренных случаев. 1и3: 2и3 На I рис 4.2 для примера представлена диаграмма разложения прямоугольных разнополярных импульсов в ряд Фурье согласно выражению 4 1

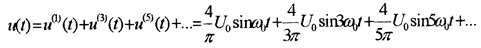
Так как функция обладает 1 и 3 видами симметрии, то в разложении присутствуют синусоидальные гармоники с нечетными порядковыми номерами (см. рис 4.2).

При анализе цепей несинусоидального тока удобно гармонический состав тока ( напряжения, ЭДС) представлять в виде амплитудного и фазового дискретных

(линейчатых) спектров.

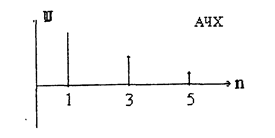
Под амплитудном линейчатым спектром понимают зависимость амплитуды тока (напряжения, ЭДС) от частоты (порядкового номера гармоники).

Под фазовым линейчатым спектром понимают зависимость фазы тока (напряжения) от частоты (порядкового номера). На рисунках показаны соответствующие амплитудный (АЧХ) и фазовый (ФЧХ) дискретные спектры.

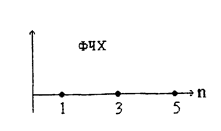
Амплитудные значения 1,3,5 гармоник и их начальные фазы при этом равны соответственно

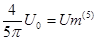
Дата добавления: 2014-11-29