Анализ переходных процессов в цепи первого порядка. 1 страница

(4.8)????????

Рассмотрим мощность в цепи несинусоидального тока.

Пусть напряжение и ток разложены в ряд Фурье:

Тогда мгновенная мощность равна

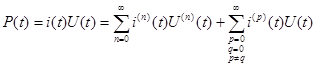(4.5)

Пользоваться понятием мгновенной мощности неудобно, так как она зависит от времени.

Найдем среднюю мощность за период, т.е. активную мощность:

,

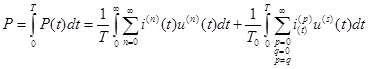где (в силу ортогональности гармонической функции)

б

где 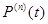-мгновенное значение мощности ‘n’-ой гармоники,

-среднее значение (активная мощность) ‘ n ’-ой гармоники

тогда с учётом последнего получим:

(4.6)

Активная мощность в цепи несинусоидального тока равна сумме активных мощностей каждой из гармоник в отдельности.

Кроме понятия активной мощности рассматриваем понятие полной мощности

где ????????

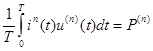
(4.7) ???????

и реактивной мощности:

Последняя равна алгебраической сумме реактивных мощностей каждой гармоники. Отношение активной мощности к полной называется коэффициентов мощности:.

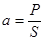коэффициент мощности.

-т.е. а всегда меньше COS(фи) для основной гармоники

Активная мощность в цепи несинусоидального тока больше активной мощности в цепи синусоидального тока за счет наличия дополнительных высших гармоник.

В цепи несинусоидального тока присутствует также мощность искажений

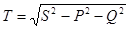(4.10)

которая получается в силу разного гармонического состава кривых тока и напряжения.

Для оценки формы кривых напряжения и тока используется ряд коэффициентов, при этом рассматриваются кривые, в которых отсутствует постоянная составляющая.

Коэффициент формы определяется как отношение действующего значения к среднему за период:

(4.11)

для синусоиды

Коэффициент амплитуды равен отношению максимального значения к действующему:

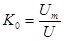(4.12)

для синусоиды ,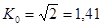

Коэффициент гармоник характеризует совокупную величину высших гармоник и равен отношению действующего значения высших гармоник к действующему значению основной:

(4.13)

По стандарту для промышленной сети коэффициент гармоник не должен превышать 5%.

5. Матричный метод анализа цепей 5.1. Законы Кирхгофа в Матричной форме

При анализе сложных электрических цепей целесообразно использовать матричный метод, основанный на представлении топологии цепи и ее параметров таблицами чисел - матрицами. Матричный метод позволяет записать уравнения цеп наиболее компактных форме, а также систематизирует и упрощает процесс их формирования. Достоинства матричного метода особенно проявляются при использовании ЭВМ, так как он позволяет получить алгоритмы формирования уравнений цепей и упростить их решение на ЭВМ.

Матричный метод базируется на классической теории цепей и опирается на законы

Кирхгофа, справедливые для любых цепей (линейных и нелинейных) с сосредоточенными параметрами.

Уравнения закона токов (ЗТК) и закона напряжений (ЗНК) Кирхгофа определяются только схемами соединения ветвей и не зависят от их физического содержания. Поэтому для записи уравнений Кирхгофа в матричной форме достатоно¹ располагать только направленным графом схемы и представить его, а также выбран переменные (токи и напряжения ветвей) в виде матриц.

Важным требованием, предъявляемым к уравнениям цепи, является их независимость - ни одно уравнение системы не должно являться линейной комбинацией остальных уравнений. Получение линейно независимых уравнений цепи как в классической так и в матричной формах обеспечивается применением теории графов, являющейся частью математической дисциплины - топологии (см. подразд. 2.4).

5.1.1.Закон токов Кирхгофа. Матрицы вершин и сечений

Уравнение ЗТК для i - го узла (сечения) можно представить в следующем

виде:

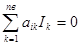k=1,2….

где коэффициент аik = + I, если k-я ветвь выходит из i -го yзла; аik = -I, если она входит в i -и узел и аik = 0, если k -я ветвь не соединяется с i -м узлом.Отметим, что число слагаемых в уравнении (5.1.) всегда равно числу ветвей схемы nв.

Если записать уравнения ЗТК для всех n y узлов, то получим систему следующего вида:

для синусоиды

Коэффициент гармоник характеризует совокупную величину высших гармоник и равен отношению действующего значения высших гармоник к действующему значению основной:

По стандарту для промышленной сети коэффициент гармоник не должен превышать 5%.

5. Матричный метод анализа цепей 5.1. Законы Кирхгофа в Матричной форме

При анализе сложных электрических цепей целесообразно использовать матричный метод, основанный на представлении топологии цепи и ее параметров таблицами чисел - матрицами. Матричный метод позволяет записать уравнения цеп наиболее компактных форме, а также систематизирует и упрощает процесс их формирования. Достоинства матричного метода особенно проявляются при использовании ЭВМ, так как он позволяет получить алгоритмы формирования уравнений цепей и упростить их решение на ЭВМ.

Матричный метод базируется на классической теории цепей и опирается на законы

Кирхгофа, справедливые для любых цепей (линейных и нелинейных) с сосредоточенными параметрами.

Уравнения закона токов (ЗТК) и закона напряжений (ЗНК) Кирхгофа определяются только схемами соединения ветвей и не зависят от их физического содержания. Поэтому для записи уравнений Кирхгофа в матричной форме достатоно¹ располагать только направленным графом схемы и представить его, а также выбран переменные (токи и напряжения ветвей) в виде матриц.

Важным требованием, предъявляемым к уравнениям цепи, является их независимость - ни одно уравнение системы не должно являться линейной комбинацией остальных уравнений. Получение линейно независимых уравнений цепи как в классической так и в матричной формах обеспечивается применением теории графов, являющейся частью математической дисциплины - топологии (см. подразд. 2.4).

5.1.1.Закон токов Кирхгофа. Матрицы вершин и сечений

Уравнение ЗТК для i - го узла (сечения) можно представить в следующем

виде:

где коэффициент аik = + I, если k-я ветвь выходит из i -го yзла; аik = -I, если она входит в i -и узел и аik = 0, если k -я ветвь не

соединяется с i -м узлом.

Отметим, что число слагаемых в уравнении (5.1.) всегда равно числу ветвей

схемы nв.

Если записать уравнения ЗТК для всех n y узлов, то получим систему следующего вида:

которую легко записать в матричной форме. Для этого обозначим матрицу коэффициентов размером (ny nв) через [Во] и столбцовую матрицу токов [Iв] Тогда (5.2) примет следующий вид:

[Bo][lв]=0. (5.3) Матричное уравнение (5.3) выражает уравнение ЗТК для всех узлов схемы

Матрица [bo ] называется полной матрицей вершин, a [Iв] - матрицей токов ветвей.

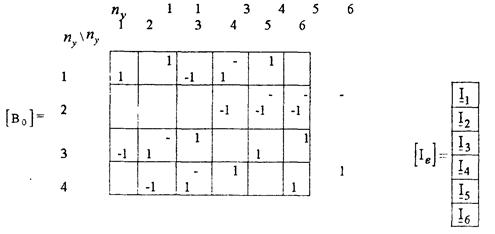
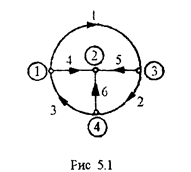
Для примера запишем матрицы [bo ] и [Iв] для графа, изображенного на рис 5 1. и имеющего nу =4, nв =6.

Оставшаяся после удаления базисной строки матрица размером (i

1)хnв обозначается [В] и называется

матрицей вершин. Выражение

[B][lв]=[0] (5.4)

представляет собой уравнена ЗТК в матричной форме.

Для графа (рис.5.1.) выбрав базисным узел 4, получим:

Уравнения ЗТК приобретают более удобный и упорядоченный вид, если для их записи выбрать не независимые узлы, а главные сечения и условиться о определенной процедуре нумерации ветвей и сечений. При записи матричного уравнения ЗТК выбирают дерево графа, затем нумеруют по порядку: вначале все (!!!ci!!!) от 1 до (nв - п у +1), а потом ветви дерева от (nв - n у +1) до nв обозначают все

главные сечения, число которых равно (ny -1), и задают их направления, совпадают

с направлениями пересекаемых ветвей дерева Затем аналогично матрице I [B] составляется матрица сечений[ С] размером (п y -1)х nв. Знаки элементов

матрицы [ C] определяются относительно направлений сечений. Если направление ветви совпадает с направлением сечения - записывается +I, если не совпадает - (-I), если ветвь не входит в данное сечение записывается ноль

Составим для примера матрицу сечений для графа рис. 5.2

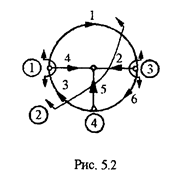
Особенностью матрицы [ С] является то, что ее можно представить в виде двух блоков - матрицы [G] и единичной матрицы размером (ny -1)х(ny -1), как это показано в (5.5.).

Отметим, что матрицы [ G] и [В] содержат полную информацию о графе.

Это означает, что, располагая матрицей [ G] или матрицей [ В], можно восстановить графы схемы.

Умножив матрицу [ С] слева на матрицу токов ветвей [iв ], получим аналогично (5.4) выражение ЗТК в матричной форме

5.1.2. Закон напряжений Кирхгофа. Контурная матрица.

Уравнение ЗНК для i - го контура можно представить в ином

виде

где bi k = +I, если направление k -ой ветви совпадает с направлением обхода контура, bi k = -1 - если эти направления не совпадают, и bi k = 0, если k -я ветвь не входит в i -и контур. Если записать уравнения ЗНК для всех nU =(nв-ny +1) главных контуров

графа, то получим систему уравнений следующего вида:

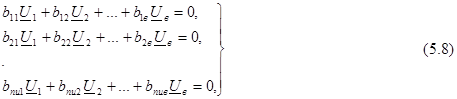
Левую часть системы уравнений (5.8) удобно представить в виде произведения двух матриц: матрицы коэффициентов bi k размером (nв - п y + 1)х nв

виде контурной матрицы [ К] и столбцовой матрицы напряжений ветвей [Uв ]:

Последнее равенство (5.9) представляет собой выражение ЗНК в матричной

форме.

При составлении матрицы [ К] для упорядочивания ее элементов следует придерживаться следующего порядка: вначале выбирается дерево графа и производиться нумерация ветвей в прежнем порядке - в начале связи, а потом ветви дерева, затем по порядку (по номерам связей) обходятся главные контуры в направлениях связей.

Напомним, что под Uk, понимается напряжение k -и ветви, т.е. условно

выделенного в общем случае активного двухполюсника, или напряжение на зажимаx обобщенной ветви, как это показано, например, на рис. 5.3.

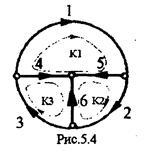
В качестве примера составим матрицы [К] и [Uв ] для графа, изображенного

на рис.5.4 и содержащего nв =6 и ny=4. Поэтому [К] имеет размер 3х6, а [Uв] -6х1:

Общим свойством матрицы [К], которое является следствием выбранной процедуры ее составления, является то, что она всегда содержит блок в виде

единичной матрицы [1св] размер которой равен числу связей. Остальную часть матрицы [ К] обозначим [ F], и тогда контурная матрица

5.2.Уравнения ветви. Обобщенная ветвь.

Для сокращения числа уравнений цепи (размеров матриц) и получения наиболее общих результатов, рассмотрим в качестве ветви схему (рис. 5.3), называемую обобщенной ветвью.

Аналитическая связь между током I. и напряжением Uk ветви, выражен

через ее параметры, называется уравнением ветви.

Запишем для обобщенной ветви уравнения по ЗНК и ЗТК

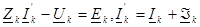
и подставив второе уравнение в первое, получим выражение

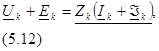
представляющее собой уравнение к -и ветви.

Заметим, что если ветвь не содержит источников (источник тока разомкнут источник ЭДС замкнут накоротко), то получим

Для схемы, содержащей nв не связанных между собой ветвей, мы можем записать

следующих правил знаков. Если направление ветви совпадает с направлением ЭДС, она записывается со знаком плюс, а если эти направления не совпадают - минус

(рис. 5.5). При определении знака источника рассматривается контур, составленный из источника и параллельной ветви.

Этот контур обходят в направлении этой ветви (рис. 5.6). Если выбранное направление обхода контура совладает с 3, то его записывают со знаком плюс, и если не совладает - со знаком минус.

Кроме того (5.13) содержит диагональную матрицу называемую матрицей сопротивлений ветвей.

Равенство (5.13) можно решить также относительно токов:

Равенство (5.13), также как и (5.14), являются уравнением ветви. Иногда их называют уравнениями закона Ома в матричной форме.

5.3.Метод токов связей (контурных токов)

Вначале, на примере графа (рис.5.4), покажем справедливость следующего равенства:

представляющего собой связь между токами ветвей и контурными токами. Здесь [Ik] - матрица контурных токов, элементами которой являются контурные токи (токи ветвей связи), число которых равно nв = nв - n у +1

Для графа (рис. 5.4)с использованием контурной матрицы (5.10) получим

Первые nв - nу +1 строк полученной матрицы отражают в себе тот факт, что контурные токи равны токам связей. Остальные nу -1 строк определяют токи деревьев

по уравнениям ЗТК, записанным для главных сечений. Следовательно, после перемножения получается матрица токов ветвей.

Напомним, что в уравнениях контурных токов переменными являются ток связей. Для получения таких уравнений воспользуемся (5.13). Умножим все члены

этого равенства слева на матрицу [ К] и учтем, что

Теперь исключим из последнего выражения токи ветвей (выразим их через контурные токи) при помощи (5.15) и получим окончательно

представляющее собой матричное уравнение контурных токов. Правая часть (5.16) учитывает все источники ЭДС и токов, действующих вцепи. В левой части тройное матричное произведение

представляет собой матрицу контурных сопротивлений [Zk]. Действительно, для примера (рис 5.4), используя (5.10) и учитывая, что

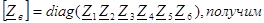
Расчет цели методом контурных токов выполняется в следующем порядке: в

начале по (5.1 б) вычисляется матрица контурных токов [Ik], а затем по (5.15) - токи [Ik]

ветвей [Iв] Обычно для этих вычислений используются стандартные программы ЭВМ и некоторых отечественных программируемых калькуляторов.

5.4. Метод узловых напряжений

Покажем вначале на примере справедливость следующего матричного равенства

Равенство (5.17) устанавливает связь между напряжениями ветвей и узловыми напряжениями при условии, что базисный узел выбран за опорный.

Для графа схемы (рис. 5.1 и 5.7), используя полученную ранее матрицу [ В], при базисном узле 4 имеем

Каждая строка полученной матрица определяет напряжение соответствующей ветви через узловые напряжения по ЗНК.

т.д. Следовательно, она является матрицей

напряжений ветвей [Uв]. Для записи

матричного уравнения узловых напряжении воспользуемся уравнением ветви форме (5.4) и умножим его

на матрицу [ B] слева. Учтем также, что

Исключим теперь напряжения ветвей [Uв ] при помощи (5.17) и получим окончательно

представляющее собой уравнение узловых напряжений в матричной форме Правая часть (5.18) учитывает источники токов и преобразованных

источников ЭДС. Тройное матричное произведение

в левой

части равно матрице контурных проводимостей схемы. Для схемы рис. 5.7 в этом не трудно убедиться, если воспользоваться полученными выше [B] и [B]^е, а так матрицами учесть, что

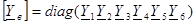
По методу узловых напряжении расчет выполняется порядке следующем:

вначале определяются узловые напряжения [Uy] (из 5.18), затем матрица напряжений ветвей по (5.17), а потом матрица токов ветвей из (5.14).

5.5. Метод напряжений ветвей дерева

Учитывая аналогию уравнений ЗТК через матрицу вершин [В] [Iв] =0 и матрицу сечений [ C][Iв] = [ 0], можно получить уравнение, аналогичное матричному уравнению узловых напряжений (5.18), заменив в нем матрицу вершин | В | на

матрицу сечений [С ]. При этом количество независимых переменных nу -1 не

изменится, а в качестве переменных будут использоваться не узловые напряжения, а напряжения ветвей выбранного дерева графа. Действительно, если

, то аналогичное уравнение, записанное через матрицу сечений

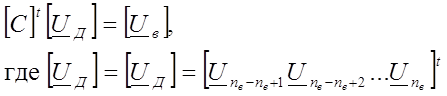
столбцовая матрица напряжений ветвей дерева.

В качестве примера запишем уравнение (5.19) для графа (рис. 5.8) с использованием матрицы [С ], записанной ранее (5.5)

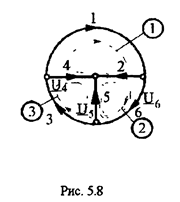
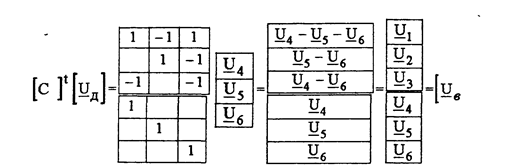
Первые три строки полученной матрицы - напряжения 1,2 и 3 ветвей связи, определяемые по уравнениям ЗНК, записанных для главных контуров 1,2 иЗ (рис 5. Остальные строки тривиально определяют напряжения ветвей дерева.

Используя уравнения (5.6) (5.14) и (5.19), получим уравнение, аналогичное уравнению узловых напряжений (5.18)

которое называется матричным уравнением напряжений ветвей дерева. Вычисление токов ветвей [Iв ] осуществляется аналогично методу узловых

напряжений.

Уравнения узловых напряжений и напряжений ветвей дерева аналогичны и совпадают в том случае, если все ветви графа имеют общую точку, и она выбрана в качестве опорного узла (о) (рис. 5.9).

Основные определения, понятия. Законы коммутации.

Переходные процессы возникают в электрических цепях при переходе из одного режима в другой в следствие подключения источников в сеть, отключения от нее, изменения параметров сети или ее топологии. Любая причина, вызывающая переходный процесс, называется коммутацией.

В большинстве случаев переходные процессы возникают после срабатывания механического или электронного переключателя, работу которого сопровождают весьма сложные явления - горение дуги, перенос носителей в полупроводнике, пробой изоляции и другие- Учет всех этих факторов представляет собою трудную и часто практически неразрешимую задачу. Поэтому при анализе переходных процессов реальное устройство представляется схемой замещения, отражающей рассматриваемые физические процессы с достаточной для практики точностью. В результате получают идеализированную расчетную модель цепи, содержащую сосредоточенные параметры - активное сопротивление, индуктивность, емкость, взаимную индуктивность и идеализированный ключ мгновенного действия. Предполагается, что процесс переключения таким ключом совершается мгновенно за время Dt->0, в течение которого его сопротивление изменяется мгновенно от бесконечности до нуля при включение и от нуля до бесконечности - при выключение.

Задача исследования переходных процессов состоит в определение в мгновенных значений напряжений U(t), токов i(t), потокосцепдений y(t)

и т.п. после коммутации. Обычно момент коммутации совмещается с началом отсчета времени t =0. Момент времени непосредственно предшествующий коммутации обозначают t = 0^- и непосредственно после

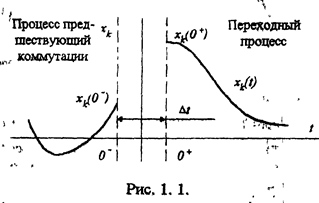
На рис. 1. 1 представлена кривая некоторой переменной напряжение тока и т.п.) хk(t) до и после коммутации. Расчету подлежит функция x_k(t) при t>=0⁺. Она определяется, как решение системы

интегродифференциальных уравнении цепи образующихся после коммутации, с учетом состояния цепи, предшествующего коммутации x_k(0^-).

Классический метод анализа переходных процессов состоит в формирование и последующем решение системы обыкновенных линейных дифференциальных уравнений цепи. Они должны составляться для цепи

после коммутации на основе законов Кирхгофа или с применением методов токов связей, узловых напряжений с использованием уравнений элементов, приведенных в табл1.

Таблица 1 Уравнения элементов

Затем полученные уравнения необходимо привести к одному

дифференциальному уравнению относительно искомой переменной.

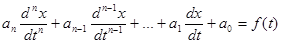В общем случае будем иметь неоднородное дифференциальное уравнение n-го

порядка, линейное с постоянными коэффициентами:

(Неоднородное уравнение, так как правая часть f(t)¹0).

Как известно из математики решение неоднородного уравнения складывается из двух решений:

x(t)=х'(t)+х"(t), (2)

где х'(t) = хуст(t)-частное решение неоднородного уравнения, которое в

электротехнике носит понятие установившейся (вынужденной) составляющей;

x"(t) = x_св(t) -общее решение однородного дифференциального уравнения

Для определения установившейся составляющей необходимо рассчитать цепь любым методом расчета в новом установившемся режиме. Для нахождения свободной составляющей, необходимо определить корни xapaктеристического уравнения a1, a2,... an и постоянные интегрирования A2...An так как общее решение однородного уравнения записывается следующим образом

Составим характеристическое уравнение. Для этого необходимо первую производную заменить на a, вторую- a², а n- производную на aⁿ B соответствии с выражением (2) имеем

Решая (3), найдем корни характеристического уравнения. Свободная составляющая всех реакций с течением времени затухает, так как энергия электрических полей емкостей и магнитных полей индуктивностей цепи убывает при выключенных источниках. Как видно из (3), для этого необходимо, чтобы вещественные части всех корней характсристического уравнения были отрицательны Re[ak]<0, т.е. корни должны быть либо отрицательными вещественными, либо комплексными сопряженными с отрицательной вещественной частью.

Дата добавления: 2014-11-29