Анализ переходных процессов в цепи первого порядка. 2 страница

Произвольные постоянные интегрирования А1,А2,..,Аn находятся с использованием начальных условий-значений переменных или их производных в момент времени t= 0*.т.е. сразу после коммутации. Требуемое число начальных условий равно числу определяемых постоянных интегрирования или порядку, цепи п. Постоянные интегрирования А1,А2,..,Аn определяются из условий Коши, то есть необходимо знать выражения и начальные значения (числи) для функции'^ (п-1)- ой ее производных. При этом используются так называемые законы коммутации. Законы коммутации отражают тот физический факт, что энергия как магнитного поля индуктивности, тем и электрического поля емкости мгновенно (скачком) изменится не может, В противном случае мощность в такой цепи (при скачкообразном изменении энергии) должна быть бесконечно большой, что не может быть. Таким образом, энергия магнитного поля индуктивности и электрического поля емкости изменяются во время коммутации непрерывно. Поэтому, так как энергия магнитного поля в индуктивности,

то, если во время коммутации L=const, то чтобы не изменилась энергия достаточно, чтобы

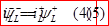
то есть ток в индуктивности во время-коммутации скачком измениться не может(ток в индуктивности до коммутации равен току индуктивности после коммутации). Условие (4) выражает закон коммутации тока в индуктивности. Если во время коммутации меняется величина индуктивности, то необходимо рассматривать более общий закон коммутации, гласящий,что потокосцепление контура во время коммутации скачком измениться не может:

Энергия электрического поля емкости как известно, равна

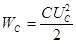
Поэтому имеем следующий закон коммутации для емкости:

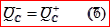
напряжение емкости во время коммутации скачком изменится не может(напряжение на емкости до коммутации равно напряжению емкости после коммутации). В случае, если емкость меняется во время коммутации, то говорят о более общем законе: заряд узла, содержащего емкости, скачком изменится не может

После определения свободной и установившейся составляющих окончательно записывают решение дифференциального уравнения в соответствии с выражением (2).

В некоторых случаях для оценки сложности решаемой задачи представляет интерес определение, порядка цепи n. Как известно из курса математики, порядок цепи (порядок системы дифференциальных уравнений) равен числу независимых начальных условий. Отсюда следует, что порядок цепи может быть определен по числу независимых начальных условий.

Так как напряжения на индуктивностях

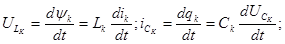
и токи в емкостях определятся первыми производными по времени, то наибольший порядок цепи равен суммарному числу индуктивностей и емкостей, включенных в цепь. Обозначим это число NLC. Однако индуктивности и емкости могут соединятся между собой так, что их начальные токи и напряжения окажутся зависимыми. Рассмотрим сечение цепи, которое включает в себя только ветви с индуктивностями и с источниками тока (рис. 2).

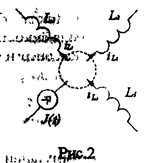
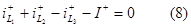
По ЗТК для него можем записать уравнение в момент времени t-=0⁺ из которого следует, что

одно т начальных условий является зависимым и такая подцепь имеет порядок не третий (по числу индуктивностей), а второй. Такое сечение, содержащее только ветви с индуктивностями и с источником тока, называют индуктивным. Еслицепь содержит NL I таких сечений, то порядок цепи n=NLC-NLI

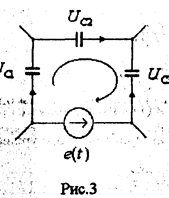
Рассмотрим контур схемы, состоящей из емкостей и источников напряжения, изображенный на рис.3, и запишем для него уравнение ЗНК

в момент времени t=0⁺

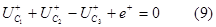Из этого уравнения следует что одно из начальных условий зависимо и рассматриваемая подцепь имеет порядок не третий (по числу емкостей), а второй. Такой контур, образованный только емкостями и источниками напряжений, называют емкостным. Если цепь содержит N_CE таких контуров, то порядок уменьшается на это число. Итак в общем случае порядок цепи

В качестве примера определим порядок цепи, изображенной на рис. 4. Здесь имеем N_LC=9, два емкостных контура и два индуктивных сечения, указанных на рисунке. Поэтому получим n =9-2-2=5. Заметим, что порядок цепи может оказаться меньше, чем вычисленный по (10) вследствие определенного соотношения параметрами схемы.

2.1. Общий случай

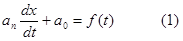Цепь первого порядка с одним независимым источником описывается уравнением

Записываем общее решение

Приравнивая правую часть в (1) к нулю, получим однородное уравнение

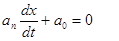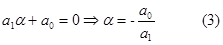а затем из характеристического уравнения находим его корень

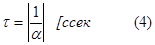то есть корень характеристического уравнения один и он обязательно отрицательный, что характерно для пассивной цепи. Величина обратная корню характеристического уравнения, взятого по модулю,

носит название постоянной времени.

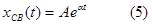Записывая свободную составляющую в виде

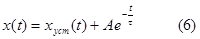и подставляя (5) в (2) с учетом (4), имеем

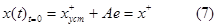Решение (6) должно удовлетворять начальным значениям при t=0

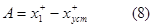где х⁺_уст - значение установившейся составляющей реакции в начальный момент, х⁺-начальное значение реакции. Откуда постоянная интегрирования

Подставляя (8) в (6), записываем окончательно решение неоднородного дифференциального уравнения:

Таким образом определяется решение для любой цепи первого порядка. Как видно из (9), в цепи первого порядка переходный процесс полностью характеризуется постоянной времени.

Рассмотрим подробнее понятие постоянной времени цепи. Для этого рассчитаем и построим график кривой свободной реакции цепи первого порядка хсв, = Ае^wt. В табл.2 приведены расчетные значения для конкретных значений времени t, кратных постоянной времени т, а на рис.2.1 в соответствии с данными табл.2 построен график сводной реакции.

Таблица 2

t		1t	2t	3t	4t
e^-t/^t		0.368	0.87	0.95	0.98
1- e^-t/^t		0.632	0.13	0.05	0.02

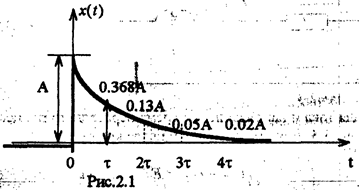
Как видно из рис 2.1 и табл.2, при t=3t сводная реакция составляет 0.05А (5%) от начального значения,при t=4t -0.02A (2%) от начального значения, т.е. с погрешностью 5% для первого случая и 2% для второго случая можно считать, что сводная составляющая равна нулю и в цели имеет место установившейся режим работы. Поэтому постоянная времени характеризует длительность переходного процесса. Теоретически переходный пороцесс продолжается бесконечно долго, реально длительность переходного процесса T_nn

принимается равной 3-4 t, T_nn @(3-4)t.

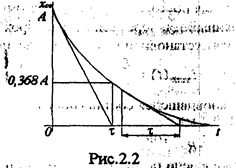
Так как отрезок подкасательной в любой точке кривой Ае ^–t/t равен постоянной величине t (см. рис: 2.1) и имеет размерность времени, то значение величины t определяет скорость затухания свободной реакции, т.е. скорость изменения тока или напряжения во время переходного процесса. Экспериментально постоянная времени t определяется либо как абсцисса точки на кривой сводной реакции (рис 2.2), ордината которой равна 0.368А, либо как отрезок, отсекаемый подкасательной на оси абсцисс подкасательной, г. с. постоянная времени численно равна отрезку времени в течении; которого ток либо напряжение изменяются в е раз. Итак,в цепи первого порядка вид и длительность переходного процесса полностью определяется постоянной времени t. Причем при включении цепи одной и той же топологии (конфигурации) на источник постоянного или переменного, гармонического напряжения постоянная времени одна и таже, так как является величиной, обратной корню характеристического уравнения, взятому по модулю.

Рассмотрим конкретные случаи переходных процессов в цепи первого порядка.

2.2. Включение цепи RL на источник постоянного напряжения

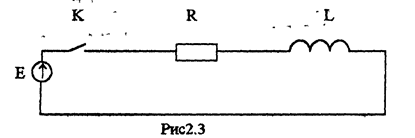
Определим закон изменения тока и напряжения во время переходного процесса в цепи, изображенной на рис.3.3. Для этого для цепи после коммутации составим уравнение по ЗНК.

Будем иметь:

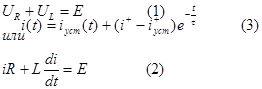общее решение в соответствии с выражением (9) раздела 3.1, имеет вид:

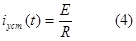Найдем установившуюся составляющую тока. Для этого составим эквивалентную расчетную схему для цели в новом установившемся режиме работы. Если источник постоянный, то необходимо закоротигь ветви с индуктивностями (ul=o для постоянного тока) и разомкнуть ветви с емкостями(ic=0 -постоянный ток через емкость не проходит); из расчета полученной схемы находят установившуюся составляющую.

Начальное значение установившейся составляющей

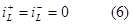Начальное значение тока в цепи по закону коммутации

так как до коммутации ток в цепи не протекал.

Найдем постоянную времени цепи для данного случая. Характеристическое уравнение имеет вид

Откуда постоянная времени для цепи с индуктивностью

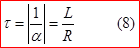Исходя из (3) с учетом (4)-(6), (8), записываем окончательно выражение для тока (реакции) во время переходного процесса

или

Найдем изменение напряжения на индуктивности

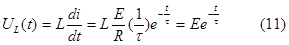
В соответствии с полученными выражениями на рис 2.4а,б построены зависимости тока и напряжения индуктивности во время переходного процесса при включении цепи RL на источник постоянного напряжения.

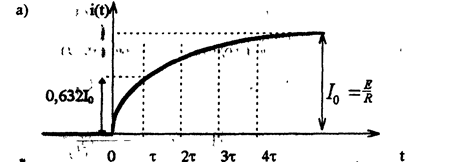
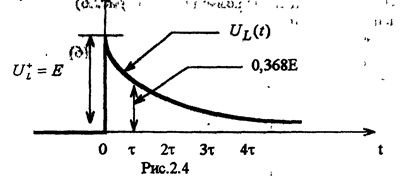
Ток и напряжение изменяются по экспоненциальным законам. При этом, ток индуктивности изменяется непрерывно, а напряжение индуктивности в момент коммутации имеет скачок напряжения U+L=E, равный напряжению источника. Постоянная времени может быть найдена по кривой тока (возрастающей экспоненциальной зависимости) как абсцисса точки, ордината которой равна 0,632I_о от установившегося значения тока.

Для убывающей экспоненциальной зависимости -как абсцисса точки, ордината которой равна 0,368 от начального значения.

2.3???

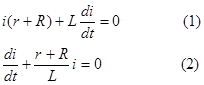Во время коммутации ключ переводится из положения 1 в 2 т.е цепь. отключается от источника и замыкается на добавочное сопротивление R. Для цепи после коммутации уравнение по ЗНК имеет вид.

или

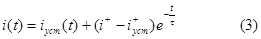
т.е. получили однородное дифференциальное уравнение с постоянными коэффициентами. Как известно, общее решение записывается в следующем виде

(производную di/dt заменяем на a)

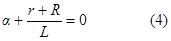
Составим характеристическое уравнение

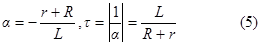
откуда

Из закона коммутации с учетом схемы цепи до коммутации (см. рис2.б) начальное значение тока в цепи (при t=0)

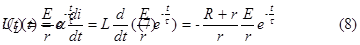Так как в новом установившемся режиме цепь отключена от источника, то установившаяся составляющая реакции равна нулю iycт=O, поэтому также начальное значение установившейся составляющей iyст = 0 С учетом (6) общее решение (3) имеет вид

При этом напряжение

Как видно из рис.2.7, во время коммутации напряжение на индуктивности имеет

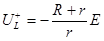1 скачок напряжения (перенапряжение)

, которое может значительно превосходить напряжение источника.

Пример. Напряжение источника Е=12В. Сопротивление катушки r= 1 Ом.

Добавочное сопротивление R=1 кОм. Тогда начальное значение напряжения на катушке (перенапряжение на катушке)

Такое напряжение может привести к пробою межвитковой изоляции, вызвать межвитковое короткое замыкание, искрение контактов переключателя, горение дуги, т.е. привести к аварийному режиму работы. Поэтому при отключении больших индуктивностей необходимо предусмотреть меры по снижению начального перенапряжения на индуктивности реостатное выключение, шунтирование индуктивности гасящими цепочками (см.рис.2.8)

2.4 Переходный процесс в цепи RL при включении на синусоидальное напряжение

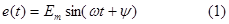Пусть напряжение источника изменяется по следующему закону

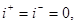где y-начальная фаза, определяющая момент коммутации и называемая фазой включения. В этом случае по-прежнему начальное значение тока

а установившиеся значения тока определяется

где j=arctg(wL/R) - угол сдвига между током и напряжением. Тогда подставляя найденные значения в общее решение для цепи первого порядка (3) предыдущего раздела получим

Вид переходного процесса в этом случае определяется не только постоянной времени, но и существенно зависит от фазы включения y. Если y-j=0, то свободный ток i_св(t)=I_msin(y-j)e^-t/t =0 и переходный процесс отсутствует, сразу после включения наступает установившейся режим. если же y-j=p/2, то i_св(t)=I_me^t/t имеет наибольшее значение в начальный момент времени. В этом случае ток в цепи во время переходного процесса

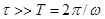Кривая тока при условии, что

имеет, приведена на рис.2.6, из которого видно, что в цепи образуется сверхток I_mm £2I_m. Величина сверхтока I_mm тем больше, чем больше постоянная времени t.

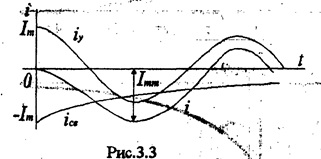
Электродинамическая сила, как известно, пропорциональна квадрату тока. Поэтому во время переходного процесса она может возрасти до 4 раз по сравнению со значением в установившемся режиме работы. Для нелинейной индуктивности (трансформатора) сверхток возрастает в десятки раз, следовательно, силы в сотни раз. Поэтому, чтобы исключить их механические повреждения, необходим бандаж для обмоток и для магнитопровода (стяжки).

Пепреходный процесс в цепи RL при включении на синусоидальное напряжение

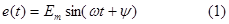Пусть напряжение источника на входе цепи (рис 2.9) изменяется по следующему закону

где y-начальная фаза, определяющая момент коммутации и называемая фазой включения. В соответствии с ЗНК, составленного для цепи после коммутации, имеем неоднородное дифференциальное уравнение первого порядка

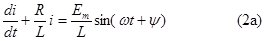либо в нормальной форме

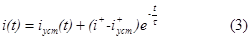Как известно можно записать

Установившеюся составляющую тока найдем из расчета цепи (см. рис 2.10) на основе метода комплексных амплитуд.

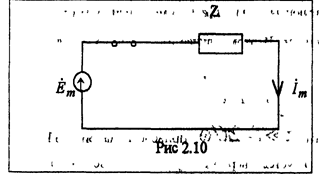
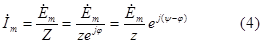По закону Ома:

Где комплексное сопротивление цепи

Исходя из (4), записываем мгновенное значение установившегося тока

и значение установившейся составляющей при t=0

В соответствии с законом коммутации ток индуктивности скачком измениться не может, поэтому начальное значение тока в цепи

так как до коммутации ток в цепи не протекал.

Найдем постоянную времени. Из уравнения (3).приравнивая правую часть нулю, получим однородное уравнение

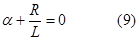
которому соответствует характеристическое уравнение

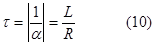
Откуда постоянная времени

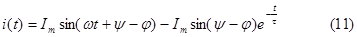
Записывая окончательно решение уравнения в соответствии с выражением (3) и с учетом (10),(7),(б),(5) будем иметь.

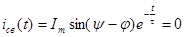
Вид переходного процесса в этом случае отделяется не то времени, но и существенно зависит от фазы включения y. Если y- j = 0, то свободный ток

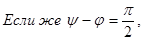
и переходный процесс отсутствует, сразу после включения наступает установившейся режим.

то свободная составляющая

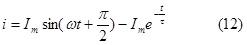
имеет наибольшее значение в начальный момент времени. В этом случае ток в цепи во время переходного процесса

Кривая тока при условии, что t»T=2p/w, приведена на рис.2.11, из которого видно, что в цепи образуется сверхток I_mm£2I_m. Величина сверхтока I_mm тем больше, чем больше постоянная времени t.

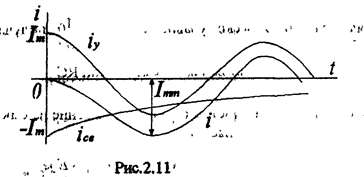
Электродинамическая сила, как известно, пропорциональна квадрату тока. Поэтому во время переходного процесса она может возрасти до 4 раз по сравнения со значением в установившемся режиме работы. Для нелинейной индуктивности (трансформатора) сверхток возрастает в десятки раз, следовательно, силы в сотни раз. Поэтому, чтобы исключить механические повреждения обмоток и шихтованного магнитопровода, необходим бандаж для обмоток и для магнитопровода (стяжки). Мощные трансформаторы (индуктивности) включают при фазе включения y- j = 0,, чтобы отсутствовал переходный процесс и сразу наступал установившейся режим работы.

2.5 Включение цепи RС на постоянном напряжении

В соответствии ЗНК iR +Uc = Е и учитывая, что ток I = С(dU_c)/dt имеем следующее неоднородное дифференциальное уравнение для цепи

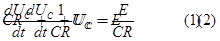
или в нормальной форме

Общее решение запишем в следующем виде

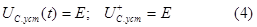
Напряжение на емкости в новом установившемся режиме и его значение при t=0 равны, соответственно

В соответствии с законом коммутации напряжение емкости во время коммутации

скачком измениться не может, поэтому

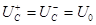
т.е. пусть до коммутации на емкости имелось начальное значение Uo.

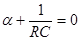
Составляя характеристическое уравнение получаем

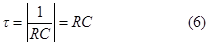
Постоянная цепи RC:

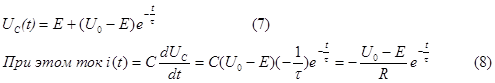
В соответствии с (3) и с учетом (4) - (6) напряжение на емкости во время переходного процесса изменяется

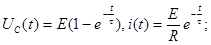
На рис. 2.13. в соответствии с (7) и (8) построены напряжение емкости и ток в цепи для трех случаев в зависимости от начального напряжения емкости.

1-й случай. Заряд емкости: Пусть напряжение Uo=0, из выражений (7) и (8)

2-й случай. Дозаряд емкости: Начальное напряжение емкости 0 < Uо < E тогда напряжение и ток изменяются в соответствии с выражениями (7) и (8). При этом как видно из выражения (8), ток при дозаряде минимальный.

3-й случай перезаряд емкости: Uо < 0 напряжение емкости отрицательное но по модулю IUoI < Е

Как видно полученных кривых, в начальный момент времени при включении цепи RC имеет место скачок тока, i⁺=-(Uo-E)/R, величина которого значением источника ЭДС E, начальным напряжением на емкости Uo и активным сопротивлением цепи R. При этом наибольшее значение скачок тока имеет место при перезаряде емкости, что необходимо учитывать при включении конденсаторов (необходимо подключать сопротивления, ограничивающие ток заряда емкости).

Перенапряжений ЗАМЕЧАНИЕ

Если рассмотреть энергетические процессы при включении цепи RC на источник постоянного напряжения, то окажется, что за время переходного процесса 50% энергии источника выделяется на активном сопротивлении в виде тепла, а 50% запасается в виде энергии электрического поля емкости, т.е. КПД такого устройства 50 %. Другими словами, если необходимо запасти в конденсаторе энергию 1 Дж, то от источника будет потреблена энергия в 2 Дж, энергия в 1Дж будет выделена в виде потерь на соединительных проводах.

2.6 Коротеое замыкание цепи RC

Ключ во время коммутации из положения 1 переводится в 2 (см рис 2.14). Исходя из ЗНК для цепи после коммутации, iR + U с = О дифференциальное уравнение относительно напряжения емкости имеет вид:

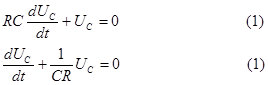
Составляя характеристическое уравнение

и определяя его корень, найдем постоянную времени цепи RC

В соответствии с законом коммутации начальное напряжение на емкости U⁺_c=U^-_c; = E. Так как после коммутации цепь отключается от источника, то установившиеся напряжение U_с.уст (t) == U⁺_c.ycrn ⁼ S. Теперь, исходя из общего решения (см. выражение (3) раздела 2.5.), окончательно записываем решение
дифференциального уравнения и находим ток цепи.

Дата добавления: 2014-11-29