Задачи статики. Аксиомы статики

СТАТИКА

Исходя из определения раздела статики, можно представить две основных задачи статики: задача о приведении системы сил к простейшему виду и задача о равновесии системы сил.

В первой задаче данную систему сил приводят к более простому виду. Методами статики систему сил любой сложности можно привести к одной или двум силам.

Вторая задача ставится в тех случаях, когда равновесие твердого тела имеет место или необходимо определить условия, при котором это равновесие наступит. Условия равновесия устанавливают зависимости между всеми силами, приложенными к твердому телу.

В основе раздела статики лежат аксиомы, которые были сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы классической механики являются одновременно и аксиомами статики. Представим данные аксиомы.

1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны (рис. 2).

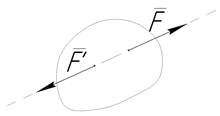
Рисунок 1.1

3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил.

Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление.

Таким образом, силу можно переносить в любую точку по линии действия, не изменяя ее модуля и направления. Поэтому в статике твердого тела сила рассматривается как скользящий вектор. Данным результатом можно пользоваться в случае определения условий равновесия и не рассматриваются внутренние усилия.

4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис. 5).

(1.1)

Рисунок 1.2

Модуль силы R будет равен:

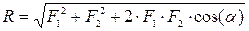(1.2)

где α — угол между направлениями сил F₁ и F₂.

Сила R является равнодействующей сил F₁ и F₂. Однако это явление сохраняется только в том случае, если силы приложены в одной точке. В общем случае сила R называется геометрической суммой векторов.

5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.

Эта аксиома утверждает, что силы действия друг на друга двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Таким образом, в природе не существует одностороннего действия силы. Так же данная аксиома утверждает, что при взаимодействии две любые части тела действуют друг на друга с равными по модулю и противоположно направленными силами, которые образуют уравновешенную систему сил.

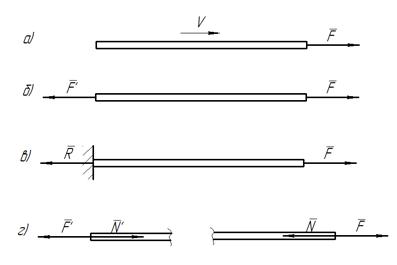
Рисунок 1.3

Рассмотрим данное положение на следующем примере. Пусть стержень растягивается с некоторой силой F. Если силу приложить только к одному концу, то произойдет движение стержня (рис. 1.3а), т.е. нарушится равновесие. Чтобы этого не произошло необходимо к другому концу приложить равную по модулю силу F’, но противоположно направленную (рис. 1.3б), или закрепить второй конец (рис. 1.3в). Однако и во втором случае будет возникать некоторая сила R, называемая реакцией связи, которая уравновесит силу F.

Если же мы мысленно рассечем стержень на две части, то и эти части будут уравновешенны. Так как в этом случае необходимо рассматривать и возникающие внутренние усилия в стержне N и N’, которые стремятся сжать стержень обратно (рис. 1.3г). Внутренние усилия образуют взаимно уравновешенную систему сил, поэтому при решении задач статики они не рассматриваются.

6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении.

Принцип аксиомы заключен в следующем. Если деформируемое тело находится в равновесии и, соответственно, под действием внешних сил оно не изменяет более свой размер, то при составлении условий равновесия данной тело можно принять как абсолютно твердое.

Дата добавления: 2014-11-29