
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задачи С4
|
|
|
|
Пример С4а
Задание. На угольник ABC (угол ABC=90°), конец A которого жестко заделан, в точке C опирается стержень DE (рис. 5.10). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена сила F1 и пара с моментом M, а к угольнику – равномерно распределенная на участке KB нагрузка интенсивностью q и сила F2.
Дано: F1=10кН, F2=20кН, M=5кНм, q=20кН/м, a=0,2м.
Определить: реакции в точках A, C, D, вызванные заданными нагрузками.
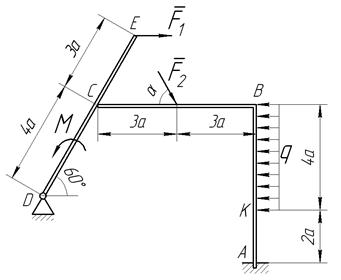
Рисунок 5.10
Решение.
Рассматриваемая конструкция состоит из двух тел – угольника и стержня. Соответственно для решения задачи можно составить шесть уравнений равновесия, по три каждого тела. В точке A находится заделка. Данная связь имеет три составляющие реакции. В точке D – неподвижный шарнир, т.е. две составляющие реакции. Связь стержня DE в точке C является вариантом гладкой поверхности. Соответственно имеем еще одну неизвестную. Реакция направлена перпендикулярно поверхности DE. Количество неизвестных равно количеству уравнений равновесия, поэтому задача является статически определимой.
В данной задаче для определения реакций наиболее удобно разделить конструкцию на части. Полученный результат с реакциями в опорах показан на рисунке 5.11. Реакция N характеризует воздействие угольника на стержень. Реакция N’, наоборот, воздействие стержня на угольник. Силы равны по модулю и направлены в противоположные стороны. При рассмотрении конструкции целиком, данные силы будут являться внутренними и компенсировать друг друга.
Распределенная нагрузка заменена на эквивалентную сосредоточенную силу Q, приложенную по центру распределения. Модуль силы Q будет равен:
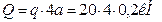 .
.

Рисунок 5.11
На угольник действуют четыре неизвестные реакции, на стержень три. Поэтому вначале рассматриваем равновесие стержня. Составляем уравнения равновесия:
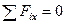 ,
, 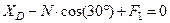 , (1)
, (1)
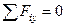 ,
, 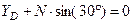 , (2)
, (2)
 ,
, 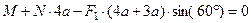 , (3)
, (3)
Из уравнения (3):
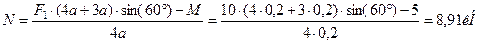
Из уравнения (2):
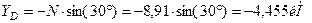
Из уравнения (1):
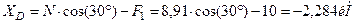
После определения N, в угольнике остаются неизвестными так же три реакции. Составляем теперь уравнения равновесия для данного тела:
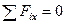 ,
, 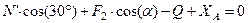 , (4)
, (4)
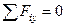 ,
, 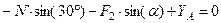 , (5)
, (5)
 ,
,
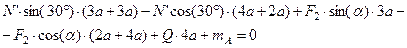 (6)
(6)
Из уравнения (4):

Из уравнения (5):
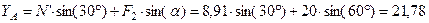
Из уравнения (6):
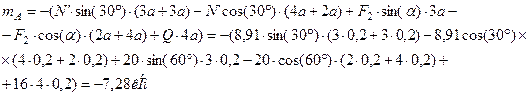
Ответ: XD=-2,284кН, YD=-4,455кН, N=8,91кН, XА=-1,716кН, YA=21,78кН, mA=-7,28кНм.
Пример С4б
Задание. Конструкция состоит из двух ломаных стержней и представляет собой трехшарнирную арку (рис. 5.12). В точках А и В находятся шарнирные неподвижные опоры, в точке С – шарнир. На левый стержень действует сила F1 и пара с моментом М, а на правый равномерно распределенная нагрузка интенсивностью q и горизонтальная сила F2.
Дано: F1=15кН, F2=10кН, M=6кНм, q=30кН/м, a=0,3м.
Определить: реакции в точках A, B, C вызванные заданными нагрузками.

Рисунок 5.12
Конструкция состоит из двух стержней, т.е. можно составить шесть уравнений равновесия, по три для каждого стержня. В опорах А и В по две неизвестных составляющих реакций опор. В точке С шарнир, в котором возникают две пары взаимноуравновешенных сил. Силы XC и YC выражают действие левого стержня на правый, а X’C и Y’C наоборот, действие правого на левый (рис. 5.13). Задача является статически определимой, так как количество неизвестных соответствует количеству уравнений равновесия.
Для решения задачи разделим конструкцию на части, приложим соответствующие реакции связей и заменим распределенную нагрузку на эквивалентную сосредоточенную силу Q, приложенную по центру распределения. Модуль силы Q будет равен:
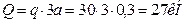 .
.

Рисунок 5.13
Составляем условие равновесия правой части:
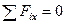 ,
,  , (1)
, (1)
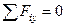 ,
,  , (2)
, (2)
 ,
,
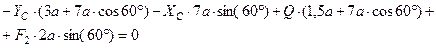 , (3)
, (3)
В полученных уравнениях четыре неизвестных. Определить реакции опор для правого стержня пока невозможно. Составляем условия равновесия для левого стержня.
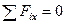 ,
,  , (4)
, (4)
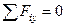 ,
, 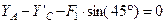 , (5)
, (5)
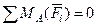 ,
,
 , (6)
, (6)
В данной системе также четыре неизвестных. Поэтому требуется рассматривать систему из шести уравнений, учитывая, что 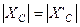 и
и 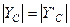 .
.
Для упрощения расчетов 3 и 6 уравнения были составлены так, чтобы в них были по две одинаковые неизвестные реакции. Составим из данных уравнений систему, заменив X’C и Y’C на XC и YC соответственно:
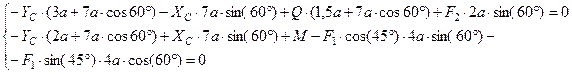
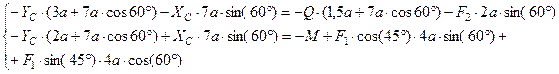
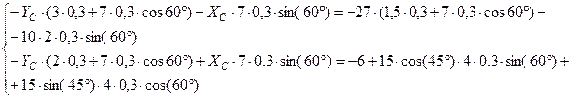
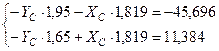
Решив данную систему уравнений, получим 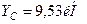 ,
, 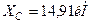 .
.
Подставляя найденные значения реакций в уравнения (1), (2), (4), (5) определим остальные неизвестные.
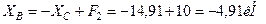 ,
,
 ,
,
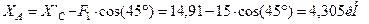 ,
,
 .
.
Ответ: XA=4,305кН, YA=20,135кН, XB=-4,91кН, YB=17,47кН, XC=14,91кН, YC=9,53кН.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 2383; Нарушение авторских прав?; Мы поможем в написании вашей работы!