Примеры решения задач. Определить равнодействующую и центр параллельных сил P и Q (рис

Задача 7.2.1

Определить равнодействующую и центр параллельных сил P и Q (рис. 7.2а), если модули сил равны P=15Н, Q=10Н, а расстояние между точками приложения сил AB=10м.

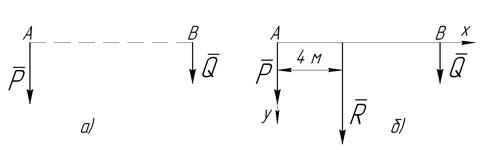
Рисунок 7.2

Решение.

Проведем оси Ox и Oy вдоль линии AB и перпендикулярно ей соответственно. Модуль равнодействующей параллельных сил определяем как сумму данных сил:

Центр параллельных сил (точки приложения равнодействующей) будет находиться на линии АВ. Координату точки определим формуле (7.1):

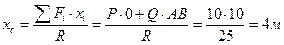
Откладываем от начала координат вдоль оси Ox 4 м (рис. 7.2б).

Ответ: R=25Н, xC=4м.

Задача 7.2.2

Определить равнодействующую и центр параллельных сил P и Q (рис. 7.3а), если силы направлены в противоположные стороны, их модули равны P=15Н, Q=10Н, а расстояние между точками приложения сил AB=10м.

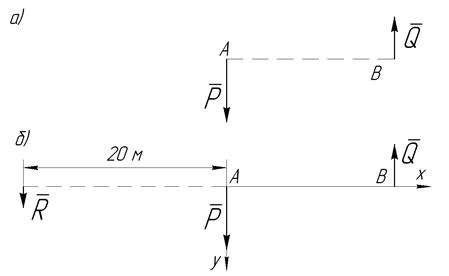
Рисунок 7.3

Решение.

Аналогично с предыдущей задачей проводим оси координат и определяем модуль равнодействующей, учитывая направление сил:

.

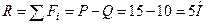Определяем положение центра параллельных сил, считая направление сил вдоль оси Oy положительным, а обратно - отрицательным:

.

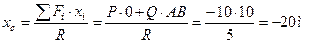Откладываем от начала координат вдоль оси Ox в отрицательном направлении 20 м (рис. 7.3б).

Ответ: R=5Н, xC=-20м.

Задача 7.2.3

Определить в координаты цента тяжести кронштейна, состоящего из однородных стержней AB=0,2м, BD=0,1м и DE=0,06 м, имеющих одинаковых линейный вес (рис. 7.4).

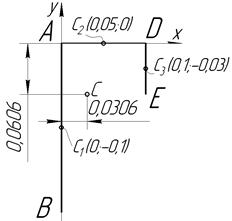
Рисунок 7.4

Решение.

Обозначим центы тяжести однородных стержней и найдем их координаты. Определим положение центра тяжести по формулам (7.4):

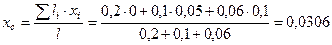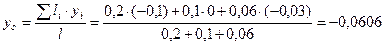м,

м.

Обозначаем центр тяжести С на рисунке.

Ответ: x_C=0,0306м, y_C=-0,0606м.

Задача 7.2.4

Из однородной пластины в виде треугольника ОАВ с основанием ОВ=60см и высотой ОА=45 см вырезан полукруг радиуса r=20см (рис. 7.5). Определить в координаты центра тяжести полученной фигуры.

Рисунок 7.5

Решение.

Определяем площади фигур. Для треугольника ОАВ:

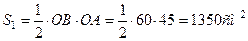
Для кругового сектора:

,

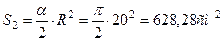где α – угол сектора в радианах, α=π.

Координата центра тяжести треугольника находится на пересечении медиан. Эта точка делит каждую медиану в соотношении 2:1. Для нахождения центра тяжести прямоугольника достаточно от катетов отложить по 1/3 длины другого катета. Соответственно координаты центра тяжести треугольника ОАВ:

, .

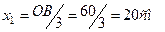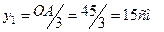Определяем координаты центра тяжести кругового сектора. Центр лежит на оси симметрии сектора, т.е. .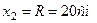

Ординату центра тяжести получим по формуле:

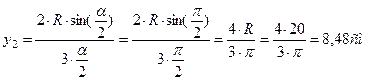
Определяем центр тяжести всей фигуры, учитывая, что вырезы берутся с отрицательным знаком:

,

.

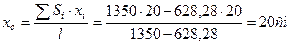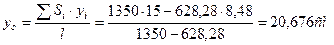Обозначим центр тяжести на рисунке.

Ответ: X_C=20 см, Y_C=20,676см.

Задача 7.2.5

Определить высоту H однородного прямоугольного параллелепипеда из условия, чтобы центр тяжести тела, состоящего из однородных пирамиды и параллелепипеда находился в плоскости ABCD (рис. 7.6). Высота призмы H₁=1,2м.

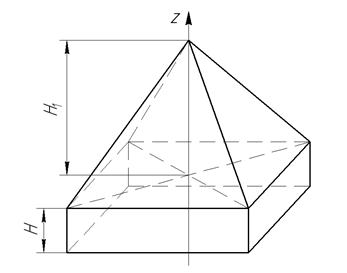
Рисунок 7.6

Решение.

Проведем ось z по оси пирамиды. За отметку «0» принимаем точку пересечения оси с основанием ABCD.

Объем пирамиды определяется как 1/3 произведения площади основания на высоту, а координата центра тяжести на расстоянии 1/4 высоты от основания, т.е. в нашем случае:

, .

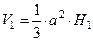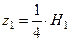Объем параллелепипеда и координата центра тяжести по оси Z:

, .

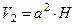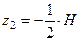Центра тяжести тела должен иметь координату z=0:

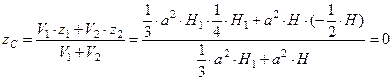
Выражение равно нулю, если числитель равен нулю:

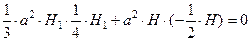
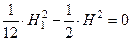
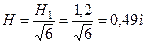
Ответ: H=0,49м

Дата добавления: 2014-11-29