Определение вероятностей состояния полнодоступного пучка. 2 страница

Определение вероятностей состояния системы. Процесс изменения состояний (i =0, 1, 2,...) рассматриваемой коммутационной системы можно рассматривать как марковский процесс рождения и гибели со счетным множеством состояний, так как за бесконечно малый промежуток времени [ t, t +t)с вероятностью более нуля в состояние i возможен только непосредственный переход системы из состояний i –1, i, i +1.

Для процесса рождения и гибели (занятий и освобождений) со счетным множеством состояний стационарные вероятности состояний определяются, выражениями (4.12). Поскольку в рассматриваемой задаче на обслуживание поступают вызовы простейшего потока, то параметр потока занятий l _i= l, i =0, 1, 2,.... Параметр потока освобождений

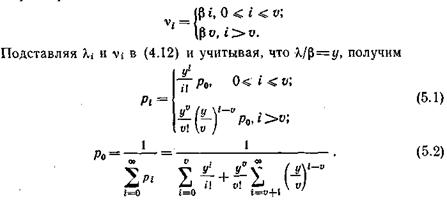
Практический интерес представляет случай с конечной очередью, т. е. l _i <n _i, i> u.Отсюда l < ubи y< u.Учитывая это и используя выражения для суммы бесконечно убывающей геометрической прогрессии, преобразуем (5.2) к виду

Стационарные вероятности состояний (5.1) с учетом (5.3) запишутся в следующем виде:

Заметим, что при ограничении числа состояний коммутационной системы 0£ i £u, т. е. при переходе к системе с потерями ф-ла (5.4) для определения вероятности p_i приводится к первой формуле Эрланга (4.21) – E_{i, u}(y).

Сопоставим значения вероятности состояний p_i в системе с ожиданием и вероятности состояний E_{i ,u}(y) в системе с потерями. С этой целью разделим числитель и знаменатель соотношения

т. е. для систем с ожиданием время нахождения в состояниях, когда поступающие вызовы немедленно обслуживаются, меньше, чем для систем с потерями.

Рекуррентное соотношение (4.31) p_i=p_{i -1}(y / i),полученное для систем с потерями, сохраняется и для систем с ожиданием при i £u.Несколько иной характер имеет рекуррентное соотношение для вероятности того, что на ожидании находится точно r +1 вызовов:

Из этого соотношения, имея в виду, что y< u, следует w₀ > w₁ > >w₂>..., т. е.вероятность того, что в пучке заняты все линии и на ожидании нет вызовов, больше, чем вероятность того, что на ожидании находится точно один вызов, а последняя вероятность больше, чем вероятность того, что на ожидании находятся точно два вызова, и т. д.

В системах с ожиданием потери по времени p_t есть доля времени, в течение которой все uлиний пучка заняты и на ожидании находится r =0, 1, 2,... вызовов. Исходя из этого, потери по времени равны вероятности р (g>0) того, что поступивший вызов не будет немедленно обслужен, а будет ожидать начала обслуживания в течение времени g больше нуля. Эта вероятность равна

Используя соотношение (5.5), получаем

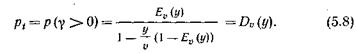
Выражение (5.8) называется второй формулой Эрланга. Формула табулирована. Таблицы позволяют по любым двум из трех параметров – у, u, p_t – определить третий.

Выражение (5.8) показывает, что потери по времени p_t, численно равные условным потерям р (g > 0),могут быть определены и с помощью таблиц первой формулы Эрланга. Используя эти таблицы, p_t можем определить из следующего соотношения:

Из (5.8), знаменатель которой меньше 1, следует, что в системах с ожиданием потери по времени больше, чем в системах с потерями. Такой вывод находится в полном соответствии и с соотношением (5.6).

В системах с ожиданием, как и в системах с потерями, при обслуживании полнодоступным пучком вызовов простейшего потока вероятность потерь по времени и вероятности состояний системы, определяемые по (5.4), зависят только от интенсивности поступающей нагрузки у иемкости пучка линий u.

Характер зависимостей между у, uи p_t. Зависимости y=f (u) при p_t =const и y=f (p_t)при u=const (и соответственно c= f (u) и c= f (p_t), где c= y /u) для систем с ожиданием имеют точно такой же характер, как и для систем с потерями (см. рис. 4.4–4.7). Однако количественные оценки этих зависимостей существенно различаются. При заданных потерях p_t величина поступающей нагрузки в системах с ожиданием должна быть меньше, чем в системах с потерями. Так, например, при потерях p_t = 0,02;0,05; 0,1 в пучках емкостью u=10¸30 линий удельная поступающая нагрузка cв системах с ожиданием соответственно на 10, 15, 20% меньше, чем в системах с потерями.

Влияние величины допустимых потерь p_t на снижение пропускной способности систем с ожиданием более наглядно показывает зависимость h =f (p_t)при u=const, где h – удельная обслуженная нагрузка. В системах с ожиданием h=c, а в системах с потерями h=c(1– p_t)=c(1– Е _u(у)). Несмотря на это, при одних и тех же значениях потерь обслуженная нагрузка в системах с потерями выше, чем в системах с ожиданием. Так, при потерях p_t= 0,2 в пучках емкостью u=4, 10 и 20 линий в системах с потерями h на 10–12% больше, чем в системах с ожиданием.

На первый взгляд кажется парадоксальным тот факт, что системы с потерями обладают более высокой пропускной способностью. Ведь с точки зрения использования коммутационных устройств (пучка линий) система с ожиданием создает более благоприятные условия – вызовы в очереди ожидают начала обслуживания и после освобождения каждая линия пучка немедленно занимается для обслуживания очередного ожидающего вызова. В системах же с потерями освободившаяся линия может некоторое время оставаться свободной и занимается только после поступления нового вызова.

Однако эти рассуждения не в полной мере отражают процессы обслуживания поступающего потока вызовов системой с ожиданием и системой с потерями. Следует учитывать также следующие два обстоятельства:

1. Соотношение (5.6) показывает, что время, в течение которого коммутационная система находится в состояниях, когда вызовы немедленно обслуживаются, больше для систем с потерями, чем для систем с ожиданием. Отсюда нагрузка, обслуженная системой с потерями, больше нагрузки, которая обслуживается немедленно системой с ожиданием (т. е. без учета обслуженной нагрузки, создаваемой ожидающими вызовами).

2. Величина поступающей нагрузки в системах с ожиданием ограничена (y< uили c<1 Эрл), а в системах с потерями такого ограничения нет. Поэтому, особенно в области больших потерь, в системах с потерями удельная поступающая нагрузка к может принимать значения значительно больше 1(c=h/(1– р)),что обеспечивает и большую величину h.

Таким образом, следует констатировать, что в области любых потерь при заданной величине потерь p_t не только поступающая, но обслуженная нагрузка в системах с потерями больше, чем в системах с ожиданием.

Естественно возникает вопрос: какие особенности систем с ожиданием обусловливают их практическое применение и в какой области коммутационной техники такие системы целесообразно использовать? В связи с этим необходимо, прежде всего, отметить различный качественный характер явных и условных потерь. В системах с потерями часть вызовов теряется (не обслуживается), в системах с ожиданием обслуживаются все поступающие вызовы, при этом часть из них с некоторой задержкой. При малых величинах потерь, исчисляемых промилле и даже несколькими процентами, абонент не ощущает неудобств. Поэтому в области малых потерь предпочтительнее система с потерями, обладающая более высокой пропускной способностью. При больших значениях потерь система с потерями не обеспечивает должного качества обслуживания абонентов и непригодна для применения.

В случае больших потерь нельзя однозначно дать оценку системам с ожиданием. Все зависит от времени задержки обслуживания вызовов, находящихся на ожидании. Необходимо, чтобы время ожидания начала обслуживания для подавляющего большинства вызовов не вызывало неудобств у абонентов. Иными словами, системы с ожиданием следует применять в тех случаях, когда для повышения использования коммутационных устройств целесообразно допускать большие условные потери (исчисляемые десятками процентов), если возможно при этом обеспечить мало ощутимое для абонентов время задержки начала обслуживания. В технике телефонной связи с ожиданием вызовы обслуживаются управляющими устройствами. Область применения систем с ожиданием подробно рассмотрена во второй части этой главы.

Функция распределения времени ожидания. Потери по времени p_t,или, что то же самое, вероятность р (g > 0)того, что поступивший вызов будет обслужен лишь после некоторого времени ожидания, не позволяют в достаточной мере характеризовать качество обслуживания коммутационной системой с ожиданием поступающего потока вызовов. Полученная характеристика p_t=p (g > 0) =D _u(y)определяет долю вызовов, обслуживание которых происходит после некоторого времени ожидания, однако не дает ответа на весьма важный с точки зрения обеспечения качества обслуживания вопрос – как распределяется время ожидания начала обслуживания для вызовов, которые попадают на ожидание. В связи с этим определим функцию распределения длительности ожидания начала обслуживания при исходных предположениях рассматриваемой задачи: показательное распределение длительности занятия, ожидающие вызовы обслуживаются в порядке очереди.

Обозначим через p (g >t)вероятность того, что вызов, поступивший в произвольный момент времени, попадет на ожидание и время ожидания будет больше t; через p_i (g >t)условную вероятность того же неравенства в предположении, что вызов поступит в момент времени, когда система находится в состоянии i, и через p_i вероятность того, что система находится в этом состоянии, т. е. в системе имеется точно i обслуживаемых и ожидающих вызовов.

Имея в виду, что в рассматриваемой коммутационной системе поступивший вызов попадает на ожидание лишь в случае, когда в момент поступления вызова в системе заняты все линии пучка и на ожидании находится r =0, 1, 2,... вызовов, т. е. система находится в одном из состояний i= u, u + 1,u+2,..., по формуле полной вероятности получим

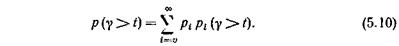
Найдем вероятность p_i (g> t) Если система находится в состоянии i (i ³u),то непосредственно перед моментом поступления вызова в системе на ожидании находится (i –u)вызовов. Поступивший вызов становится в очередь и является в очереди (i –u+1)-м. Поскольку вызовы снимаются с очереди для обслуживания в порядке поступления («первым пришел – первым обслуживается»), то вероятность p_i (g >t)есть вероятность того, что за время t после момента поступления рассматриваемого вызова будет снято с ожидания и переведено на обслуживание не более (i –u)вызовов. Исходя из этого, вероятность p_i (g >t)соответствует вероятности того, что за время t произойдет освобождение (закончится обслуживание) не более (i– u)вызовов.

Длительность обслуживания одного вызова Т (без учета времени ожидания) распределена по показательному закону

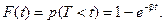
Функция распределения промежутков между моментами освобождения линий пучка при условии занятости в пучке всех uлиний есть 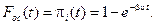Эта функция распределена по показательному закону, что определяет поток освобождений как простейший поток, параметр которого l = bu.В соответствии с этим вероятность p_j того, что за время t произойдет освобождение точно j линий, согласно формуле Пуассона составляет 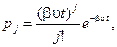а вероятность того, что за время t произойдет не более (i –u) освобождений, если система находится в состоянии i, –

Подставив соотношения (5.5) и (5.11) в (5.10) и произведя некоторые преобразования, получим

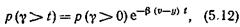
где p (g>0) определяется по ф-ле (5.8). Если за единицу измерения времени g и t принять среднюю длительность занятия, то b=1 и

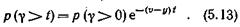
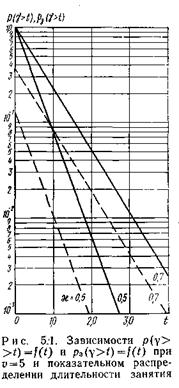Последняя формула позволяет строить универсальные семейства кривых р (g> t) =f (t)(и получить универсальные таблицы) для любых значений средней длительности занятия.

Характеристики качества обслуживания вызовов системами с ожиданием. Характер зависимости p (g >t) =f(t) при b=1 показан на рис. 5.1 для пучка u=5. Кривые построены для значений удельной поступающей нагрузки c= y /u=0,5 и 0,7 Эрл (пунктирные кривые).

Семейства кривых иллюстрируют следующие закономерности:

1. С увеличением удельной поступающей нагрузки c при фиксированной емкости пучка uкачество обслуживания ухудшается, т. е. увеличивается p (g >t) – доля вызовов, ожидающих начала обслуживания свыше заданного времени t, или для заданной величины p (g> t) увеличивается время ожидания начала обслуживания. Так, например, в пучке u=5 увеличение cс 0,5 до 0,7 Эрл при t= 1приводит к увеличению р( g>1)с 0,01 до 0,085 (в 8,5 раза) или при p (g> t)=0,01 – к увеличению t с 1 до 2,4 (в 2,4 раза).

2. С увеличением p (g >t)уменьшается время ожидания свыше заданного t при любых значениях uи c. Так, в пучке u= 5 при c=0,7 Эрл увеличение p (g> t) с 0,01 до 0,1 приводит к уменьшению t с 2,4 до 0,85 (почти в 3 раза).

Заметим, что с увеличением uпри любых значениях c и р (g >t) уменьшается значение времени t или при любых значениях cи t уменьшается вероятность p( g >t). Например, при c=0,5 Эрл и p (g> t)=0,01 увеличение u с 5 до 10 приводит, к уменьшению времени t с 1 до 0,25 (в 4 раза).

Качество обслуживания поступающего потока вызовов в системах с ожиданием также характеризуют вероятности p _з ( g >t) того, что время ожидания начала обслуживания gдля вызова, попадающего на ожидание, будет больше t, т. е. для вызовов, попадающих на ожидание,

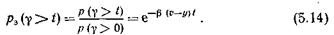
На рис. 5.1 сплошными линиями приведены кривые зависимости p _з ( g >t)=f(t). Вероятности p _з(g> t) существенно превышают вероятности p( g >t). Так, например, при u =5 и c=0,5 Эрл вероятность р _з ( g >1) в 8,5 раза превышает вероятность р( g > 1).

Ранее было установлено, что при любых значениях у иuимеет место неравенство р( g>0) >E _u (y), т. е. вероятность того, что в системе с ожиданием поступающий вызов поступает на ожидание, больше вероятности того, что в системе с потерями этот вызов будет потерян. Одной из качественных характеристик сравнения систем с ожиданием и систем с потерями является значение времени t, при котором вероятность p( g >t) численно равна E _u (y). Обозначим такое значение t через t*.

Формула (5.12) и рассмотренная зависимость р (g> t)= f (t) показывают, что с увеличением t вероятность p( g >t) уменьшается и p( g >t) ®0при t ®¥. Имея также в виду, что р (g> t)> E _u(y), можно утверждать, что при некотором значении t* имеет место равенство p( g >t *)= E _u (y), откуда p( g >t)>E _u (y) при t < t * и, наоборот, р( g >t)<E _u (у) при t>t*. Используя (5.12), определяем значение t*:

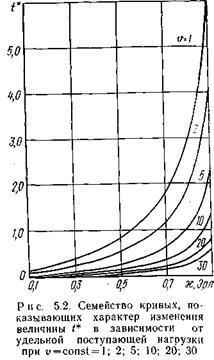
Количественная оценка величины t* иллюстрируется семейством кривых, приведенных на рис. 5.2. Эти кривые показывают характер изменения величины t* в зависимости от удельной поступающей нагрузки t *= f (c) при u = 1, 2, 5, 10, 20, 30. Для этого семейства кривых за единицу времени принята средняя длительность одного занятия, т. е. b=1. Рисунок 5.2 показывает также, что с уменьшением емкости пучка линий u и с увеличением интенсивности удельной поступающей нагрузки c повышается значение t *, при котором р(g>t*)=E _u (y).

Рассмотрим численный пример, который позволят сделать весьма важный вывод. При t* = 1 интенсивности нагрузок у, поступающих на пучки емкостью u=1, 2, 5, 10 линий, соответственно составляют 0,53; 1,34; 3,95; 8,7 Эрл. Для этих значений у по таблицам первой формулы Эрланга отыскиваем соответствующие значения E _u (y) = p (g>l)=0,34; 0,275; 0,195; 0,154. Из этого примера следует, что с увеличением u и c при определенном значении t* качество обслуживания улучшается – уменьшаются значения р (g> t *)= =Е _u (у). Однако основной вывод заключается в том, что все приведенные значения потерь в системах с потерями указывают на неудовлетворительное качество обслуживания, в то время как в системах с ожиданием при относительно малой величине среднего времени обслуживания вызова такие значения р (g>1). по существу, обеспечивают высокое качество обслуживания даже в пучке емкостью u = 1 – абоненты не замечают малые по времени задержки в установлении соединений.

К характеристикам процесса обслуживания поступающего потока вызовов в системах с ожиданием, кроме р (g>0) и р (g> t), относятся: среднее время ожидания начала обслуживания `g, отнесенное ко всем поступающим вызовам; среднее время ожидания начала обслуживания `g_зотнесенное к вызовам, попадающим на ожидание (задержанным с обслуживанием); средняя длина очереди ` r. Определим эти величины:

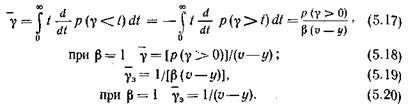
Используя (5.5) для вероятности p _{u +r} = w _r, r =0, 1, 2,..., получаем формулы, определяющие среднюю длину очереди:

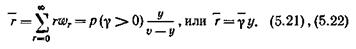
Из (5.22) следует, что средняя длина очереди определяется как среднее время ожидания начала обслуживания вызова, отнесенное ко всем поступающим вызовам, умноженное на интенсивность поступающей нагрузки.

Анализ полученных соотношений показывает, что с увеличением c и уменьшением uповышаются значения `g, `g_зи ` r. Так, например, при c=0,6 Эрл в пучке емкостью u=10 линий рассматриваемые характеристики принимают значения `g=0.02, `g<sub>з</sub>=0,25 и ` r =0,15, а в пучке u=5 линий значения этих характеристик возрастают до `g=0,12, `g_з=0,5 и ` r =0,35.

5.2. Обслуживание вызовов простейшего потока при постоянной длительности занятия

Теория Кроммелина. Исходные данные задачи такие же, как и задачи, подробно рассмотренной в парагр. 5.1. На полнодоступный пучок емкостью u(1£u£¥) линий, работающий по системе с ожиданием, поступает простейший поток вызовов с параметром l. Сохраняются предположения предыдущей задачи: вызовы, находящиеся на ожидании, обслуживаются в порядке очереди; поступающая на пучок из uлиний нагрузка у должна иметь значение, меньшее емкости пучка – y< u. Отличие заключается только в законе распределения длительности обслуживания: вместо показательного распределения полагаем длительность обслуживания каждого вызова постоянной и равной h. Длительность занятия h примем за единицу времени – h= 1. Требуется определить функцию распределения длительности ожидания начала обслуживания для любого поступающего вызова p( g >t).

Определим вначале вероятность р (g<t). имея в виду, что p (g> t)=1– p (g< t). Пусть в момент t ₀система находится в состоянии k, т. е. в таком состоянии, при котором в системе на обслуживании и ожидании находится точно k вызовов. Если k< u, то за единицу времени, равную h, коммутационная система обслужит все эти вызовы, т. е. все вызовы, находящиеся в системе в момент t ₀, к моменту (t ₀+1) покинут систему. Если же k >u, то за каждую единицу времени (рис. 5.3) коммутационная система обслуживает точно uвызовов; за время [ t ₀, t ₀+1) будет обслужено v вызовов, за время [ t ₀, t ₀ + 2)–2uвызовов,..., за время [ t ₀, t ₀+ t)– t uвызовов (в данном случае t – целое число).

Нас интересует вероятность того, что вызов, поступивший в момент t ₀, попадет на обслуживание в течение времени g, меньшего t. В момент t ₀система находится всостоянии k, рассматриваемый вызов переводит систему в состояние (k +1). Значит для того, чтобы g< t необходимо выполнение условия k+ 1£ t u + u,при этом имеется в виду, что из всех (k +1) вызовов, находящихся в системе непосредственно после момента t ₀, t _uвызовов за время t

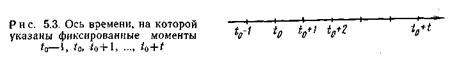
окажутся обслуженными и покинут систему, а остальные uвызовов к моменту (t ₀ +t) попадут на обслуживание. Отсюда k £ t u+u–1.

Введем обозначения: p_i(t ₀ ) – вероятность того, что в момент t ₀ система находится в состоянии i и a_k(t ₀ ) – вероятность того, что в момент t ₀ система находится в состоянии, не превышающем k:

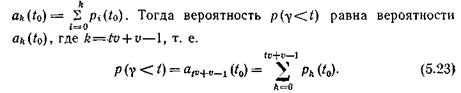
Аналогичными рассуждениями можно показать, что ф-ла (5.23) справедлива и в случае, если t – нецелое число.

Определим вероятность p_k(t ₀ ) того, что в момент t ₀система находится в состоянии k. Искомую вероятность можно представить состоящей из двух слагаемых: из вероятности p_k(t ₀ ) ₁того, что в моменты t ₀система находится в состоянии k, если в момент (t ₀–1) в системе нет очереди (k £u),и из вероятности p_k(t ₀ ) ₂того, что в момент t ₀ система находится в состоянии k, если в момент (t ₀ – 1) в системе на обслуживании находятся и и на ожидании r вызовов (k =u+ r). Рассматриваемые в момент t ₀события взаимно независимы. Поэтому p_k(t ₀ )=p_k(t ₀ ) ₁ +p_k(t ₀ ) ₂.

Определяем вероятность p_k(t ₀ ) ₁.В момент (t ₀ – 1) в системе находится не более uвызовов, вероятность этого события a u (t ₀–1). Так как длительность обслуживания каждого вызова h =1, то к моменту t ₀все эти вызовы будут обслужены и покинут систему. Ни один из вызовов, поступивших, в систему после момента (t ₀ – 1), к моменту t ₀не завершится обслуживанием и останется в системе. Для того чтобы в момент t ₀система находилась в состоянии k, необходимо поступление за время [ t ₀–1, t ₀) точно k вызовов. Согласно формуле Пуассона вероятность этого есть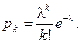

Тогда

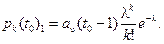
Аналогично определяем вероятность р_k (t ₀)₂. В момент (t ₀ – 1) в системе находится u +r вызовов; вероятность этого p _{u +r} (t ₀ – 1). К моменту t ₀за единицу времени систему покинут uобслуженных вызовов. Для того чтобы в момент t ₀система оказалась в состоя-

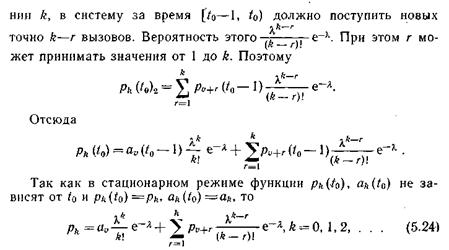
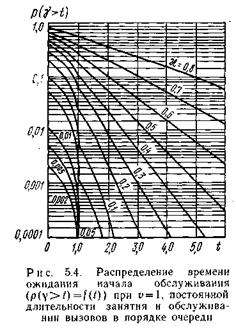Используя (5.23), находим вероятность того, что любой поступивший вызов попадет на ожидание и будет ожидать начала обслуживания больше времени t:

Система (5.24) решается методом производящих функций. Формула (5.25) для практических расчетов трудоемка. Поэтому на практике используются построенные Кроммелином семейства кривых р( g >t)= f (t) для ряда значений uиc (c =y/ u=l/u).На рис. 5.4 приведено семейство кривых для u=1.Эти кривые показывают, что характер зависимости p(y>t)=f(t) такой же, как и при показательном распределении длительности занятия: с увеличением времени ожидания g свыше заданного t уменьшается вероятность p( g >t). Однако количественные оценки рассматриваемой зависимости при постоянной и показательно распределенной длительностях занятия существенно отличаются.

Однолинейная система; произвольное распределение длительности занятия. Полячек и Хинчин, независимо друг от друга, исследовали однолинейную систему с ожиданием, на которую поступают вызовы простейшего потока с параметром l, и произвольным распределением длительности занятия. Вызовы обслуживаются в порядке очереди. Формула Полячека – Хинчина для среднего времени ожидания начала обслуживания любого вызова имеет следующий вид:

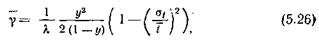
где ` t – среднее значение длительности занятия; s <sub>t</sub> – среднеквадратическое отклонение длительности занятия; у – интенсивность нагрузки, поступающей на однолинейную систему: y =l` t <1. Принимая значение t за единицу времени (` t =1), получаем

где s – среднеквадратическое отклонение длительности занятия в условных единицах. За единицу времени принята средняя длительность занятия ` t.

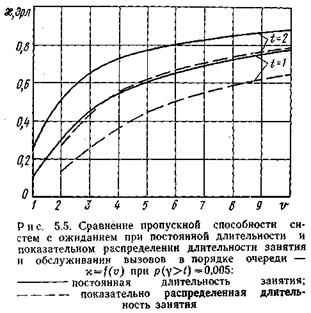При показательном распределении времени занятия s=1 ф-лы (5.27) и (5.28) соответственно совпадают с (5.18) и (5.20), так как для однолинейного пучка p( g > 0 )=y. При постоянной длительности занятия s=0

Таким образом, при постоянной длительности занятия среднее время ожидания в очереди любого вызова `gи задержанного вызова `g_з вдвое меньше, чем при показательно распределенной длительности занятия.

Дата добавления: 2014-11-29