
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение вероятностей состояния полнодоступного пучка. 4 страница
|
|
|
|
Имея в виду, что перечисленные события, приводящие коммутационную систему к моменту (t +t) в состояние (i,j,k), вза-имио независимы, можно записать
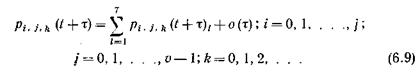
Систему уравнений вероятностей состояний модели (6.9) необходимо дополнить уравнениями, в которых состояния коммутационной системы в момент (t+ t ) характеризуются занятостью всех uлиний пучка первым и вторым этапами обслуживания вызовов, т. е. состояниями (i, u, k), в которых j =u и соответственно вероятность которых есть pi,u,k(t+ t ).
Производя над общей системой уравнений pi,j,k(t+ t ) и pi, u ,k (t+ t ) точно такие же преобразования, которые произведены в гл. 4 над системой уравнений вероятностей состояний полнодоступного пучка, обслуживающего симметричный поток вызовов, получаем систему алгебраических уравнений для определения вероятностей состояний коммутационной системы pi, j , k и pi, u ,k .
6.4. Основные характеристики качества работы системы с повторными вызовами
В качестве основных характеристик работы рассматриваемой системы примем: вероятность потери первичного вызова р и среднее число повторных вызовов, приходящихся на один первичный вызов ` c 0.
Вероятность потери первичного вызова р определяется отношением интенсивности mп потерянных первичных вызовов по причине отсутствия свободных линий в пучке в момент поступления первичного вызова к интенсивности m поступивших первичных вызовов: р =mп/m=lп/l. Поскольку поток первичных вызовов яв-
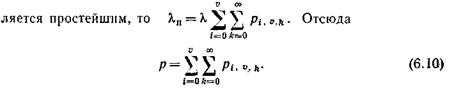
 При определении ` с 0 следует учитывать, что повторные вызовы источника вызваны как отсутствием свободных линий в пучке в момент поступления первичного и повторных вызовов, так и только первым этапом обслуживания части вызовов. Обозначим через ` c 1 среднее число повторных вызовов, приходящихся на один первичный или повторный вызов, которые происходят по причине отсутствия свободных линий в пучке в момент поступления вызова, и через ` c 2– среднее число повторных вызовов на первом этапе обслуживания. Тогда общее среднее число повторных вызовов ` c 0, осуществляемых абонентом для обслуживания одного вызова (независимо от того, закончилось ли обслуживание вызова вторым этапом либо источник отказался от дальнейших попыток добиться полного обслуживания), составляет ` c 0=` c 2+(1+` c 2)` c 1=` c 1+` c 2+` c 1` c 2.
При определении ` с 0 следует учитывать, что повторные вызовы источника вызваны как отсутствием свободных линий в пучке в момент поступления первичного и повторных вызовов, так и только первым этапом обслуживания части вызовов. Обозначим через ` c 1 среднее число повторных вызовов, приходящихся на один первичный или повторный вызов, которые происходят по причине отсутствия свободных линий в пучке в момент поступления вызова, и через ` c 2– среднее число повторных вызовов на первом этапе обслуживания. Тогда общее среднее число повторных вызовов ` c 0, осуществляемых абонентом для обслуживания одного вызова (независимо от того, закончилось ли обслуживание вызова вторым этапом либо источник отказался от дальнейших попыток добиться полного обслуживания), составляет ` c 0=` c 2+(1+` c 2)` c 1=` c 1+` c 2+` c 1` c 2.
Величина ` c 2 может быть определена из ф-лы (6.4), по которой рассчитывается среднее число попыток на первом этапе обслуживания L: ` c 2 =L –1. Тогда

 Для определения р и ` c 1могут быть использованы таблицы [24]. В этих таблицах приводятся значения р и` c 1для модели обслуживания потока вызовов, в которой учитываются повторные вызовы, появляющиеся только по причине отсутствия свободных линий в пучке в моменты поступления первичных вызовов. Значения р и ` c 1даны в зависимости от емкости пучка uпри фиксированных значениях c = l/u, T =1/r и u =g/r. Значения р и ` c 1справедливы для значений среднего времени z между двумя соседними повторными вызовами, осуществляемыми источником, и вероятности Н того, что источник производит повторный вызов, которые связаны с Т и и следующими зависимостями:
Для определения р и ` c 1могут быть использованы таблицы [24]. В этих таблицах приводятся значения р и` c 1для модели обслуживания потока вызовов, в которой учитываются повторные вызовы, появляющиеся только по причине отсутствия свободных линий в пучке в моменты поступления первичных вызовов. Значения р и ` c 1даны в зависимости от емкости пучка uпри фиксированных значениях c = l/u, T =1/r и u =g/r. Значения р и ` c 1справедливы для значений среднего времени z между двумя соседними повторными вызовами, осуществляемыми источником, и вероятности Н того, что источник производит повторный вызов, которые связаны с Т и и следующими зависимостями:

На характеристики р и ` c 0 работы системы с повторными вызовами, как и других коммутационных систем, существенное влияние оказывают величина интенсивности поступающей нагрузки у и емкость пучка линий u. Помимо того, р и ` c 0 зависят от ряда других параметров: вероятности j того, что постудивший вызов не будет полностью обслужен; вероятности H, того, что источник производит повторный вызов; среднего времени z между двумя соседними попытками источника добиться обслуживания своего вызова.
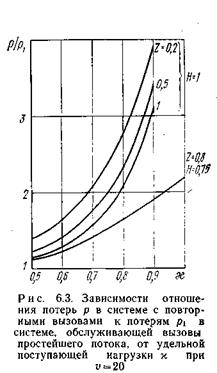
Рассматриваемые зависимости характеризуются семействами кривых ` c 0= f (c) и р/р 1 =f( c ) при определенных значениях u, j, Н и z, где c – удельная поступающая нагрузка на одну линию пучка, p 1 – потери в системе, обслуживающей простейший поток вызовов. Указанные семейства кривых приведены на рис. 6.2 и 6.3 для значений u=20; j=0,5; Н= 1и 0,75; z =0,2; 0,5; 1,0. За единицу времени величины z принята средняя длительность одного занятия ` t. Задаваясь средними длительностями первого и второго этапов обслуживания ` t =25 с и ` t =120 с, получаем при Н 1 = 1и Н 2=0,75 соответственно t 1=170 с и t 2=136 с.
Из рисунков следует, что значения ` c 0и p/p 1увеличиваются с возрастанием c, Н и уменьшением z. При этом ` c 0увеличивается более интенсивно в области больших значений c. Так, при z= 0,2 и H =0,75 увеличение cс 0,6 до 0,9 Эрл приводит к увеличению ` c 0 с 0,6 до 1,1, т. е. в 1,8 раза. Еще более ощутимо влияет на c 0 вероятность H. При c=0,9 Эрл и z =0,2 увеличение H с 0,75 до 1,0 приводит к увеличению ` c 0 в 4,3 раза.
Влияние среднего времени z на величину ` c 0 ощутимо только в области больших значений c(c>0,6 Эрл) и значений вероятности H, близких к единице. Так, при c=0,8 Эрл и H =0,75 значениям z =1,0; 0,5; 0,2 соответствуют значения ` c 0 = 0,75; 0,8; 0,9, а при H =1–` c 0=1,4; 1,55; 2,0.
На величину потерь р помимо величины удельной поступающей нагрузки х существенно влияет вероятность Н, в то время как величина z оказывает малое влияние, которое практически можно не учитывать. Так, если H =1, и z =0,5, то при c=0,5 Эрл отношение р/р 1»1,2, а при c=0,9 Эрл – р/р 1 = 3,5.
Задача.
Определить: качественные характеристики р и ` c 0 полнодоступного пучка емкостью u = 30 линий при следующих исходных данных: ` t a=20 с; ` t b=140 с; c=0,6 Эрл; j=0,4; H =0,9; z =0,09.
Решение. Определяем среднюю суммарную длительность занятия линий пучка полным обслуживанием одного вызова: t= (` t a+y` t b)/(l–j H)=162 с =0,045 ч. Значения р и ` c 1определяем по таблицам вероятностных характеристик полнодоступного пучка при повторных вызовах. Для этой цели вычисляем вспомогательные величины Т и и: T=z/H= 0,1; u=( 1 –Н) / Н»0,1.
При полученных значениях T и и, c=0,6 Эрл и u=30 выписываем из таблиц значения р и ` c 1: p =0,004; ` c 1=0,006 45. При L =l/(l–j H)=1,56 находим ` c 0 =L+ ` c 1 L– 1=0,57.
Контрольные вопросы
1. В чем заключаются основные отличия работы системы с повторными вызовами от работы систем, обслуживающих простейший и примитивный потоки вызовов?
2. Почему в системе с повторными вызовами необходимо ограничивать величину поступающей нагрузки?
3. Каковы основные параметры, влияющие на работу системы с повторными вызовами?
4. Каковы особенности составления системы уравнений вероятностей состояний системы с повторными вызовами?
5. Каковы характеристики качества работы системы с повторными вызовами, способы их определения?
6. Каковы закономерности изменения характеристик качества обслуживания р и ` c 0 в зависимости от изменения c, Н, z?
ГЛАВА СЕДЬМАЯ
Метод статистического моделирования в задачах теории телетрафика
7.1. Общие сведения
Большое число задач теории телетрафика, связанных с изучением процессов обслуживания коммутационными системами поступающих потоков вызовов, требуют исследования микросостояний коммутационных систем. К таким системам, в первую очередь, относятся неполнедоступные коммутационные системы, блокирующие звеньевые коммутационные системы, использующие ряд режимов искания и алгоритмов установления соединений. Марковские процессы позволяют достаточно просто составить системы уравнений, описывающие исследуемые процессы. Однако решение указанных систем уравнений наталкивается на большие вычислительные трудности. В качестве примера достаточно указать на наиболее простые по структуре неполнодоступ-ные схемы. Последние имеют s= 2uмикросостояний, где u – емкость пучка линий, включаемого в выходы такой системы. Напомним, что в реальных коммутационных системах u³50 и соответственно s³250>1015. Решение системы с таким числом уравнений невозможно осуществить не только на существующих ЭВМ, но и на ЭВМ ближайшего будущего. Наиболее эффективным средством решения указанных задач теории телетрафика является метод статистического моделирования.
Использование универсальных и специализированных электронных машин для решения задач теории телетрафика за последние два десятилетия нашло широкое распространение. Если на первом этапе для этих целей преимущественно создавались специализированные машины, то в последнее десятилетие, характерное бурным развитием вычислительной техники, основное применение имеют универсальные ЭВМ.
Метод статистического моделирования сложных коммутационных систем на универсальных ЭВМ или специализированных машинах сводится к имитации процесса обслуживания коммутационной системой поступающего потока вызовов, в результате которой можно получить задаваемые статистические характеристи-ки исследуемого процесса. В машине (или в приставке к ней) вырабатывается требуемого типа случайный поток вызовов, в памяти машины отображается структура моделирования коммутационной системы, моделирование производится по разработанной программе управления процессом установления соединений и их разъединения. При статистическом моделировании возможно с любой степенью точности воспроизвести весь исследуемый процесс и получить интересующие статистические характеристики. Естественно, чем выше требуется точность результатов исследуемого процесса, тем в большем объеме необходимо провести статистические испытания и, следовательно, требуется больше машинного времени.
Для экономного расходования машинного времени с сохранением высокой точности результатов моделирования непосредственное статистическое моделирование истинного процесса обслуживания коммутационной системой поступающего потока вызовов заменяется моделированием искусственных вероятностных моделей. В качестве такой модели широко используется моделирование марковской цепью.
Необходимо отметить, что в курсе «Теория телетрафика» предусматривается лишь ознакомление с основными принципами статистического моделирования. Изучение вопросов программирования и статистического моделирования – задача специального курса.
7.2. Моделирование случайных величин
Метод Монте-Карло. Моделирование случайных процессов, в том числе и систем массового обслуживания, осуществляется с помощью моделирования случайных величин, подчиняющихся различным распределениям: равномерному, показательному, нормальному и др. Для получения таких случайных величин используется случайная величина X, равномерно распределенная на отрезке [0,1], из которой различными преобразованиями получают случайную величину, подчиняющуюся требуемому закону распределения.
Случайная величина X называется равномерно распределенной на отрезке [0,1], если ее плотность f (c) на этом отрезке постоянна и равна единице:

Функция распределения такой случайной величины X имеет значения

 Плотность f (c) и функция распределения F (c) случайной величины X, равномерно распределенной на отрезке [0,1], показаны на рис. 7.1.
Плотность f (c) и функция распределения F (c) случайной величины X, равномерно распределенной на отрезке [0,1], показаны на рис. 7.1.
Случайную величину X, равномерно распределенную на отрезке [0,1], можно получить из дискретной случайной величины, равновероятно принимающей значения 0 и 1. Действительно, двоичная дробь Х=0, a –1 a –2..., где a –1 a –2... есть последовательность независимыхслучайных величин, каждая из которых с вероятностью 1/2 принимает значение 0 и с вероятностью1/2 – единицу, представляет случайную величину, равновероятно распределенную на отрезке [0, 1].
Для того чтобы промежутки между соседними значениями равномерно распределенной случайной величины X стремились к нулю, необходимо иметь бесконечную последовательность независимых случайных величин { ai, i= – 1, –2,...}, равновероятно принимающих значения 0 и 1. На практике непрерывно распределенная случайная величина моделируется приближенно. При этом может быть обеспечена сколь угодно высокая точность за счет выбора числа k двоичных разрядов в ЭВМ, определяющих двоичную дробь 0, a -1 a -2... a - k . Таким образом, вместо непрерывной случайной величины, равномерно распределенной на отрезке [0,1], моделируется дискретная случайная величина, равновероятно принимающая значения 0, 1/2 k, 2/2 k,..., 2 k –1/2 k с промежутками между соседними значениями 1/2 k.
Представим отрезок [0,1] линией, образующей окружность. Тогда случайная величина X, равномерно распределенная на отрезке [0,1], окажется равномерно распределенной по длине окружности. Получаем аналогию сигрой в рулетку. В связи с этим разнообразные модели равномерно распределенной случайной величины часто называют рулеткой, а метод статистических испытаний получил название метода Монте-Карло (по названию курорта в княжестве Монако на берегу Средиземного моря, в игорных домах которого распространена игра в рулетку).
Случайные величины X, равномерно распределенные на отрезке [0,1], можно получить тремя способами: 1) используя таблицы случайных чисел; 2) с помощью генераторов (датчиков) случайных чисел; 3) программным путем с помощью ЭВМ (псевдослучайные числа).
Псевдослучайные числа (точнее, псевдослучайная последовательность чисел) вырабатываются рекуррентным способом по специальным алгоритмам, в которых каждое последующее число получается из предыдущих в результате применения некоторых арифметических и логических операций. Эти числа называются псевдослучайными, а не случайными, так как последовательности чисел, получаемых с помощью рекуррентных соотношений, являются периодическими. Однако период может быть выбран столь большим, что практически этот недостаток можно не учитывать.
На универсальных ЭВМ используется много различных алгоритмов получения псевдослучайных последовательностей чисел, равномерно распределенных на интервале [0,1]. В них предусматривается сдвиг исходного числа на несколько разрядов влево, затем сдвиг исходного числа на несколько разрядов вправо, сложение двух новых чисел, взятие какой-либо части нового числа и другие арифметические и логические операции для получения следующего случайного числа, равномерно распределенного на отрезке [0,1].
Для увеличения периода в качестве исходных выбирается не одно, а несколько случайных чисел, используется не одно, а несколько различных рекуррентных соотношений.
Принцип моделирования непрерывной случайной величины, распределенной по любому закону. Возможность моделирования случайной величины X, равномерно распределенной на отрезке [0,1], позволяет моделировать и непрерывную случайную величину 3, распределенную по любому закону F (x)= p (X<x). Функция распределения случайной величины X монотонно возрастает от 0 до 1. Можно показать, что значения случайной величины X, распределенной по любому закону в интервале [ а, b)с плотностью f (x), определяется из уравнения

Для каждой реализации величины X решается последнее уравнение относительно x, т. е. определяется реализация величины X.
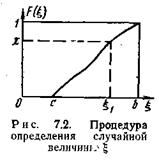 Процедура получения случайной величины x по некоторой реализации величины X показана на рис. 7.2, на котором приведена функция распределения F( x) случайной величины X. Для каждой конкретной реализации равномерно распределенной случайной величины X прямая f (x)=c пересекает кривую функции распределения только в одной точке, абсцисса которой x и определяет значение X в этой реализации.
Процедура получения случайной величины x по некоторой реализации величины X показана на рис. 7.2, на котором приведена функция распределения F( x) случайной величины X. Для каждой конкретной реализации равномерно распределенной случайной величины X прямая f (x)=c пересекает кривую функции распределения только в одной точке, абсцисса которой x и определяет значение X в этой реализации.
Покажем принцип моделирования случайной величины X, равномерно распределенной в интервале [ а, b),и случайной величины X, распределенной по показательному закону.
Равномерно распределенная в интервале [ а, b)случайная величина X имеет в этом интервале постоянную плотность, равную
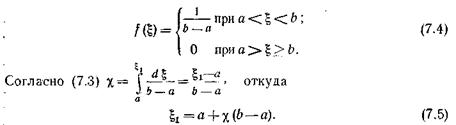
Используя в процессе моделирования каждую реализацию случайной величины X и преобразование (7.5), получаем последовательность случайных величин x, равномерно распределенных в интервале [ а, b).
Случайная величина X, распределенная в интервале [0, ¥) по показательному закону с параметром l, имеет плотность распределения

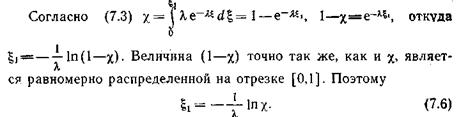
Таким образом, в процессе моделирования на основе многократной реализации случайной величины X и преобразования (7.6) получаем последовательность случайных величин x распределенных по показательному закону с заданным параметром l.
Умение моделировать непрерывные случайные величины x дает возможность моделировать и любой поток вызовов, заданный последовательностью функций распределения промежутков между вызовами. Так, при моделировании простейшего потока вызовов последовательность случайных величин zi можно получить, используя преобразование (7.6).
7.3. Моделирование коммутационных систем на универсальных вычислительных машинах
Моделирование на основе цепи Маркова процесса обслуживания потока вызовов коммутационной системой. При моделировании процесса обслуживания потока вызовов коммутационной системой, как и при моделировании любой системы массового обслуживания, нет необходимости полностью имитировать реальный процесс. Достаточно, чтобы различные состояния искусственного и реального процессов совпадали либо находились во взаимно однозначном соответствии, иными словами, достаточно, чтобы моделируемый искусственный процесс и получаемые при этом характеристики соответствовали в статистическом смысле реальному процессу и исследуемым вероятностным характеристикам.
Ранее было показано, что процесс функционирования любойкоммутационной системы при обслуживании потока с простымпоследействием (в том числе и простейшего потока вызовов) припоказательном распределении длительности занятия является марковским процессом. Поэтому вместо моделирования реальногопроцесса обслуживания потока вызовов коммутационной системойможно моделировать марковский процесс, т. е. моделировать искусственный процесс с вероятностными свойствами реального процесса. При этом модель описывается системой уравнений различных состояний обслуживающей коммутационной системы. Заменамоделирования реального процесса моделированием марковскогопроцесса приводит к существенной экономии в оперативной и постоянной памяти вычислительной машины.
При имитации моделирования реального процесса обслуживающей коммутационной системы марковским процессом требуется учитывать случайные отрезки времени пребывания системы в различных состояниях. Существенное дальнейшее упрощение статистического моделирования обслуживающей коммутационной системы достигается заменой моделирования марковского процесса моделированием цепи Маркова. При этом переход модели из одного состояния в другое происходит в дискретные моменты времени, в каждый из которых реализация случайной величины имитирует либо поступление нового вызова, либо окончание находящегося на обслуживании какого-либо вызова. Между всеми состояниями коммутационной системы и моделируемой цепи Маркова устанавливается взаимно однозначное соответствие. Это означает, что под воздействием поступившего в дискретный момент времени вызова (или окончания соединения) переход моделируемой цепи Маркова из какого-либо определенного состояния в новое соответствует переходу реальной коммутационной системы в такое же новое состояние, если до этого коммутационная система находилась в однозначном состоянии с моделируемой цепью Маркова.
При моделировании цепи Маркова каждое изменение цепи происходит за один цикл работы машины, в течение которого реализуется случайная величина, имитирующая поступление нового вызова или окончание обслуживания какого-либо ранее поступившего вызова, а также происходит переход цепи в другое состояние. Не требуется в явном виде учитывать время пребывания системы в различных состояниях. В результате уменьшаются объемы информации, которые должны храниться в памяти машины, на каждое изменение состояния обслуживающей системы требуется 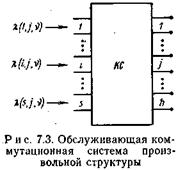 меньшее число операций машины – сокращается время цикла работы машины. Поэтому имеется возможность осуществлять на ЭВМ статистическое моделирование обслуживающих коммутационных параметров, получать значительные по объему статистические характеристики исследуемых систем и одновременно сокращать время моделирования. Для реализации каждого из событий, поступающих в дискретные моменты времени (поступления нового вызова, освобождения какого-либо соединительного пути), необходимо знать вероятности их поступления. С этой целью определим указанные вероятности и способ их реализации при моделировании на ЭВМ цепи Маркова, имитирующей обслуживающую коммутационную систему при достаточно общих предположениях.
меньшее число операций машины – сокращается время цикла работы машины. Поэтому имеется возможность осуществлять на ЭВМ статистическое моделирование обслуживающих коммутационных параметров, получать значительные по объему статистические характеристики исследуемых систем и одновременно сокращать время моделирования. Для реализации каждого из событий, поступающих в дискретные моменты времени (поступления нового вызова, освобождения какого-либо соединительного пути), необходимо знать вероятности их поступления. С этой целью определим указанные вероятности и способ их реализации при моделировании на ЭВМ цепи Маркова, имитирующей обслуживающую коммутационную систему при достаточно общих предположениях.
Коммутационная система произвольной структуры (рис. 7.3) содержит s групп входов и h групп (направлений) выходов. На каждую группу входов поступает поток с простым последействием.
Параметр потока вызовов – l (i, j, k), где i – номер группы входов; j – номер выбираемого направления; k – номер состояния коммутационной системы в момент поступления вызова. Параметр потока освобождений соединительного пути между i -й группой входов и j -м направлением при k -мсостоянии системы – n (i, j, k). Суммарный параметр потоков вызовов аk и суммарный параметр потоков освобождений bk в промежутки времени, в которые коммутационная система находится в состоянии k, составляют
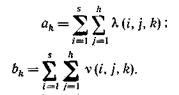
При k -мсостоянии цепи Маркова моделируется случайная величина x, равномерно распределенная на отрезке [0, ak+bk).Если в рассматриваемом цикле работы ЭВМ случайная величина x реализуется на участке равномерно распределенного отрезка [0, аk + bk), соответствующем

то полагаем, что эта случайная величина определяет поступление вызова на п -югруппу входов и соединение требуется установить в m -м направлении. Если x реализуется на участке
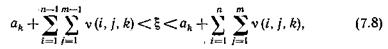
то величина x определяет освобождение соединительного пути между n -й группой входов и т -йгруппой выходов. Заметим, что при этом может освободиться любой из установленных соединительных путей между указанными группами входов и выходов.
Статистические характеристики моделирования. Целью моделирования является получение статистических оценок вероятностных характеристик процессов обслуживания коммутационными системами поступающих потоков вызовов при заданных дисциплинах обслуживания. Эти оценки принято называть статистическими характеристиками. К таким характеристикам относятся: в системах с потерями – вероятность потерь, вероятности различных состояний коммутационной системы; в системах с ожиданием – распределение времени ожидания начала обслуживания, среднее время ожидания, средняя длина очереди и другие характеристики.
Моделирование исследуемого процесса разбивается на группу п экспериментов (серий), в каждом из которых производится равное число m испытаний (например, число поступающих вызовов).
Число испытаний в каждом эксперименте выбирается таким, чтобы измеряемые статистические характеристики исследуемых вероятностных величин были бы достаточно представительны. Так, при определении вероятности потерь (ожидаемая величина которых составляет порядка 5%o) необходимо в каждом эксперименте предусмотреть десять и более тысяч испытаний, с тем чтобы число потерянных вызовов достигало нескольких десятков и даже сотен. В конце моделирования исследуемого процесса определяются средние значения, дисперсии и доверительные интервалы измеряемых статистических характеристик.
Перед моделированием первого эксперимента необходимо осуществить нулевую серию моделирования для приведения исследуемой системы в стационарный режим.
7.4. Точность и достоверность результатов моделирования
При моделировании коммутационных систем, как отмечалось выше, общее время моделирования разбивается на п равных отрезков, т. е. разбивается на п экспериментов (серий). В каждом эксперименте производится равное число т испытаний (как правило, т поступающих вызовов). Для каждой серии определяется экспериментальное значение исследуемой статистической характеристики, например потерь, по формуле

где ri – число появлений исследуемого события (число потерянных вызовов) в i -йсерии; xi – экспериментальное значение статистической характеристики (потерь) в той же серии.
После завершения процесса моделирования определяются статистические оценки среднего значения ` х, дисперсии s2 и среднеквадратического отклонения s по формулам
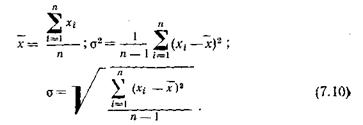
Оценка точности и достоверности результатов моделирования может быть произведена на основе применения центральной предельной теоремы для стационарных последовательностей, согласно которой исследуемые статистические характеристики сходятся к нормальному закону. При этом оценка точности и достоверности результатов моделирования производится по критерию Стьюдента:

где р (z * n -1) – доверительная вероятность или надежность статистической оценки, т. е. вероятность того, что случайный доверительный интервал ( ` х– e, ` х+ e ) содержит в себе теоретическую (достоверную) характеристику х; Sn- 1 (z*n- 1 ) – коэффициент, определяемый распределением Стьюдента при (п– 1)-й степени свободы. Величина e определяет точность статистической оценки, или доверительную границу статистической оценки.
При числе степеней свободы (п– 1)£19 и  величина S n _1(z* n _1) определяется по таблицам распределения Стьюдента.
величина S n _1(z* n _1) определяется по таблицам распределения Стьюдента.
Если число степеней свободы (n –1)>19 (т. е. число экспериментов n >20), то величину S n_1(z * n _1) можно определять по приближенной формуле

|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 597; Нарушение авторских прав?; Мы поможем в написании вашей работы!