Определение вероятностей состояния полнодоступного пучка. 8 страница

Рассуждения, которые приведены выше, дают возможность получить аналогичные системы уравнений для расчета числа соединительных устройств при использовании других типов двухзвеньевых неполнодоступных схем. Составление системы производится следующим образом. Используется формула О'Делла (9.16) в записи (9.17) и (9.18), где вместо d введена максимальная доступность двухзвеньевой неполнодоступной схемы. Для определения двух пределов нагрузки, обслуженной каждым выходом, к последующей ступени искания в рассматриваемом направлении берутся две формулы, справедливые для двухзвеньевого полнодоступного включения. Нижний предел определяется по формуле, полученной в предположении справедливости для выходов направления распределения Эрланга, а верхний предел – по формуле, использующей для выходов распределение Бернулли. Эти формулы выбираются конкретно для каждого рассматриваемого примера в зависимости от величины отношения т/п, величины q и способа отыскания свободного выхода в направлении. Все системы уравнений дают приемлемые результаты, если для заданной интенсивности нагрузки, потерь и параметров схемы число выходов к последующей ступени искания удовлетворяет следующему неравенству: mq £u£ (g/2)mq, где g – число блоков искания, объединяемых неполнодоступным включением.

9.6. Метод эффективной доступности

Метод эффективной доступности пригоден как для полнодоступных, так и неполнодоступных двухзвеньевых схем. Он основан на понятии переменной доступности, которое можно уяснить из рассмотрения схемы рис. 9.1. В режиме группового искания в выходы этой схемы включаются соединительные устройства нескольких направлений. Для подключения соединительных устройств последующей ступени, принадлежащих одному направлению, в каждом коммутаторе второго звена в общем случае может отводиться q выходов. На рис. 9.1 показано направление H_j, в котором для каждого коммутатора второго звена имеется только по одному выходу (q =1).

В рассматриваемой схеме каждому входу доступен любой выход требуемого направления только тогда, когда нет занятых соединительных путей. В этом случае доступность выходов данного направления будет максимальной (все выходы доступны) и при q =1 будет равна т. В общем случае d_max=mq.

Если занята одна промежуточная линия, то для всех входов в том коммутаторе, из которого она выходит, доступность выходов в указанном направлении уменьшится на единицу для случая q =1 и на q в общем случае, так как занятая промежуточная линия заблокирует выходы рассматриваемого направления, к которым можно подключиться с ее помощью.

При наличии i занятых промежуточных линий для всех входов в этот коммутатор, в котором имеются занятые i линий, доступность уменьшается на iq и составит величину

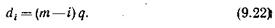
Минимальная доступность выходов рассматриваемого направления для случая сжатия (п>т) равна нулю, так как для (m +1)-го занятия, поступающего на вход коммутатора, из-за занятости всех т промежуточных линий невозможно подключение ни к какому выходу, даже при наличии свободных выходов. Для схем срасширением или без расширения и сжатия (п£т) минимальная доступность больше нуля и составляет величину

так как к моменту поступления последнего вызова (п– 1)-я промежуточная линия занята и, следовательно, доступность уменьшилась на величину (п– 1 )q. Таким образом, в процессе работы двухзвеньевой схемы в режиме группового искания доступность d_i выходов (соединительных устройств последующей ступени искания) меняется в пределах между наибольшим и наименьшим значениями:

Каждое из значений доступности d_i появляется с вероятностью W_i,где W_i – вероятность занятия i промежуточных линий из т линий, принадлежащих одному коммутатору первого звена.

Вероятность W_i можно трактовать как долю времени в течение рассматриваемого интервала, в пределах которого занято i промежуточных линий, т. е. в течение которого существует доступность d_i. Тогда работу схемы в интервал времени, в пределах которого занято i промежуточных линий, можно уподобить работе схемы неполнодоступного включения с доступностью d_i, а потери p_i, которые возникнут в это время, будут определяться значением доступности d_i. Так как значения d_i определяются соотношением (9.24), то потери р в случае включения соединительных устройств в выходы двухзвеньевой схемы будут меньше, чем при неполнодоступном включении с доступностью d_min (т. е. меньше р_тах), и больше, чем при неполнодоступном включении с доступностью d_max (т. е. больше р_тiп)

Соотношение (9.25) означает, другими словами, что рассматриваемая двухзвеньевая схема с точки зрения потерь будет хуже однозвеньевого неполнодоступного включения с доступностью d_max и лучше неполнодоступного включения с доступностью d_min.

Из этого же соотношения следует, что всегда найдутся такие два значения доступности, d_j и d_{j+ 1}, где j – целое положительное число, для которых будет справедливо

Это означает, что для данной двухзвеньевой схемы существует эквивалентное ей с точки зрения потерь однозвеньевое неполнодоступное включение. Доступность такого неполнодоступного включения с потерями, равными потерям в двухзвеньевой схеме, назовем эффективной доступностью и обозначим d _э. Из соотношения (9.25) вытекает, что

Если зависимость вероятности потерь р от доступности d при определенных значениях интенсивности нагрузки у и числа соединительных устройств последующей ступени искания uвыражается функцией

то вероятность потерь при использовании двухзвеньевой схемы запишется следующим образом:

где r = п– 1 при n £ m или r = m при n > m.

Значение р из (9.29) будет удовлетворять неравенству (9.26). Так как эффективная доступность определяется из равенства потерь, то для ее вычисления можно использовать такое соотношение:

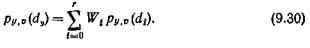
Значение эффективной доступности, определяемое из (9.30), лежит в пределах

(j – целое положительное число) и может быть дробным, причем дробное значение эффективной доступности следует понимать в смысле соотношения (9.26).

Можно показать, что если функциональная зависимость (9.28) является линейной, т. е. p=Ad + B, то из соотношения (9.30) следует, что

где ` d – математическое ожидание доступности.

В общем случае справедливо следующее соотношение для эффективной доступности:

Соотношение (9.33) по сравнению с неравенством (9.27) сужает диапазон, в котором может лежать значение d _э. Этот диапазон определяется неравенствами

Неравенство (9.34) можно записать в более удобном для вычислений виде:

где q – коэффициент, определяемый зависимостью потерь от доступности и распределением W_i (вероятностей доступности).

Минимальная доступность d_min рассчитывается по (9.23), если она не равна нулю в случаях, указанных выше. Математическое ожидание доступности

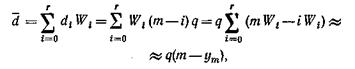
где у_m – интенсивность нагрузки, обслуженной т промежуточными линиями.

Таким образом, для определения ` d можно пользоваться следующей приближенной формулой:

Для двухсвязной схемы f =2 (см. рис. 9.2) математическое ожидание доступности можно определить из следующего выражения:

После определения эффективной доступности расчет двухзвеньевой схемы сводится к применению таблиц или формул для неполнодоступного включения. В частности, можно пользоваться ф-лой (8.36). Для заданных величин доступности и потерь эта формула является линейной зависимостью:

Выбор величины q должен производиться в зависимости от характера применяемой расчетной формулы неполнодоступного включения. При использовании (8.36) величину коэффициента q можно принимать в пределах 0,75–0,85, величины a и b см. [12].

Расчет по методу эффективной доступности производится в следующем порядке. По (9.23) определяют значение минимальной доступности d_min для случая, когда она не равна нулю. Далее по (9.36) находят величину математического ожидания доступности ` d, а затем определяют эффективную доступность d _эиз соотношения (9.35). Если d _эпо условиям точности расчетов можно заменить ближайшим целым числом, то определяют коэффициенты a и b расчетной ф-лы (9.37) в зависимости от полученной величины d _эи требуемой величины потерь. Наконец, число соединительных устройств, которое должно быть включено в выходы рассматриваемой двухзвеньевой схемы для обслуживания интенсивности поступающей на них нагрузки при заданных потерях, рассчитывается по (9.37).

9.7. Структура многозвеньевых коммутационных схем

Помимо двухзвеньевых коммутационных схем в коммутационной технике широко применяются многозвеньевые схемы. В частности, квазиэлектронные системы коммутации используют четыре – восемь звеньев соединения.

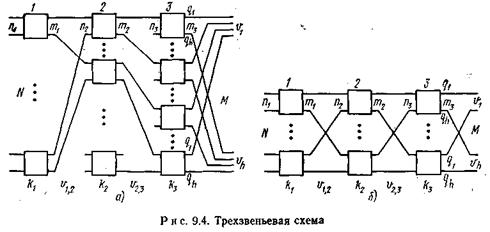
На рис. 9.4 приведена трехзвеньевая схема, показанная в двух вариантах. Если в схеме между любым из входов и любым коммутатором последнего звена имеется не более одного соединительного пути, то такую структуру называют веерной (рис. 9.4 а); если число соединительных путей более одного, структуру называют связанной (рис. 9.4 б). Обозначения структурных параметров для трехзвеньёвой схемы, приведенной на рис. 9.4, аналогичны обозначениям параметров двухзвеньевой схемы. Трехзвеньевая схема помимо режима группового искания может быть использована и в режиме индивидуального искания (кроме веерной, так как она имеет не более одного пути между заданным входом и требуемым выходом). В этом случае в каждом направлении имеется лишь один выход.

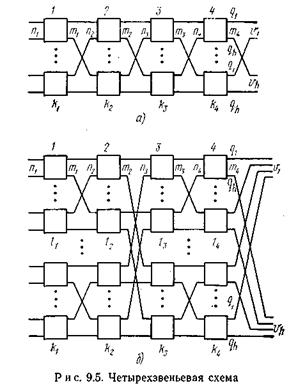
На рис. 9.5 а приведена четырехзвеньевая коммутационная схема с неделимой структурой, т. е. со структурой, которая не распадается на блоки, а на рис. 9.5 б – четырехзвеньевая схема блочной структуры. При блочном построении коммутаторы первого и второго звеньев, а также третьего и четвертого звеньев соединяются таким образом, что представляют собой отдельные двухзвеньевые блоки. Несколько таких блоков образует левую группу, находящуюся в первых двух звеньях. Аналогичное построение имеет и правая группа (третье и четвертое звенья). Левые и правые двухзвеньевые блоки связаны между собой. Схему, приведенную на рис. 9.5 б, иногда называют итерационной схемой, так как ее можно получить, заменяя каждый коммутатор двухзвеньевой схемы такой же двухзвеньевой схемой. На этом рисунке число коммутаторов в каждом звене обозначено k ₁ ,...,k ₄, aчисло коммутаторов в каждом блоке соответствующего звена обозначено l ₁,..., l ₄.

Для построения коммутационных схем с большим числом звеньев могут быть использованы те же закономерности структуры, которые показаны на примерах двух–четырехзвеньевых схем. Так, например, восьмизвеньевая схема может быть построена из нескольких четырехзвеньевых схем (см. рис. 9.5), соединенных между собой в одну общую схему. На рис. 9.6 приведен один из вариантов такой восьмизвеньевой схемы. Коммутаторы каждой пары соседних звеньев образуют двухзвеньевые блоки. Несколько двухзвеньевых блоков связывается между собой и образует четырехзвеньевую схему в соседних четырех звеньях. Такие укрупненные четырехзвеньевые блоки объединяются, в свою очередь, в восьмизвеньевую схему.

На основе рассмотренных схем легко представить себе построение схем с числом звеньев более восьми.

Существенную роль в коммутационных схемах играет отношение числа выходов к числу входов на каждом звене, которое называется коэффициентом расширения, если это отношение больше единицы, или коэффициентом концентрации, если оно меньше единицы. Для трехзвеньевой схемы, приведенной на рис. 9.4, таким образом, можно рассматривать три коэффициента: s₁=s_вх=u_1,2/ N; s₂=u_2,3/u₁,₂; s₃=s_вых= M /u_2,3. В схемах с любым числом звеньев количество коэффициентов а равно числу звеньев.

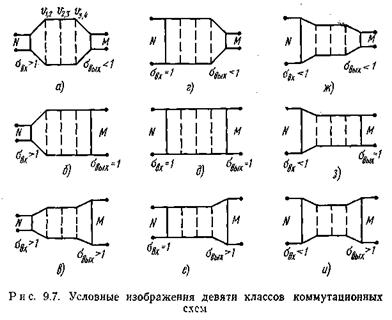В режиме группового искания, когда заданный вход схемы должен быть подключен к любому свободному выходу требуемого направления, схемы, как правило, должны иметь расширение. Особо существенную роль играют коэффициенты s_вх и s_вых, относящиеся к первому и последнему звеньям. Если считать, что во всех звеньях, кроме первого и последнего, нет ни концентрации, ни расширения (число входов в коммутаторы равно числу выходов), тогда по отношению к значениям коэффициентов концентрации или расширения на входе и выходе имеет место девять типов коммутационных схем, приведенных на рис. 9.7. Условные изображения схем показаны применительно к четырехзвеньевым схемам.

Первые три типа схем (схемы а–в) относятся к случаю, когда на входе схемы (в первом звене) имеется расширение. Последние три типа (схемы ж–и) – это схемы с концентрацией на входе, а остальные три типа схем не имеют ни концентрации, ни расширения в первом звене. Каждой из схем в этих трех группах соответствуют три возможных значения коэффициента s_вых в последнем звене (на выходе).

Естественно, что коммутационные схемы связанной структуры, имеющие более двух звеньев, могут использоваться в режиме индивидуального искания, т. е. в таком режиме, когда заданный вход, на который поступает вызов, должен быть подключен к одному вполне определенному выходу.

9.8. Способы межзвеньевых соединений и методы искания в многозвеньевых схемах

Вероятность потерь в звеньевых блокирующих коммутационных схемах зависит от многих факторов. В первую очередь она зависит от характера потока вызовов и величины поступающей нагрузки. Существенная зависимость вероятности потерь наблюдается от структуры коммутационной схемы: размеров коммутаторов, числа промежуточных линий между коммутаторами, наличия или отсутствия расширения (концентрации) в каждом из звеньев, наличия или отсутствия блоков, веерной или связанной структуры и других характеристик структуры. Установлено также, что вероятность потерь зависит от способа межзвеньевых соединений л метода искания свободных промежуточных линий (выбора пути установления соединения для поступающего вызова).

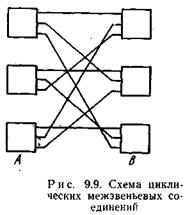
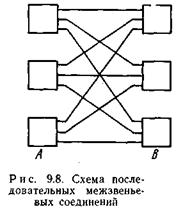
В звеньевых коммутационных схемах наиболее часто используются два способа межзвеньевых соединений, показанных на рис. 9.8 и 9.9. На первом рисунке изображен способ последовательных межзвеньевых соединений, при котором номера занимаемых входов в коммутаторах звена В соответствуют номеру коммутатора в звене А. На втором рисунке приведен способ циклических межзвеньевых соединений. При этом способе осуществляется циклический сдвиг номера занимаемого входа в коммутаторах звена В при переходе от одного выхода из коммутатора звена А к другому. Любой из указанных двух способов соединений при неделимой структуре может применяться независимо от другого между любой парой соседних звеньев. При блочной структуре каждый из способов может использоваться как внутри блока, так и для междублочных соединений. Таким образом, для схемы с несколькими звеньями число вариантов межзвеньевых соединений может быть значительным.

Методами искания, наиболее часто применяемыми в коммутационной технике, считаются: последовательное искание из фиксированного исходного положения, последовательное искание из случайного положения. Второй из этих способов дает такие же результаты, как и равновероятное случайное искание (равновероятный выбор любой свободной промежуточной линии).

Каждый из указанных методов искания может независимо от другого использоваться между любой парой звеньев как внутри блоков, так и на междублочных промежуточных линиях.

9.9. Расчет многозвеньевых коммутационных схем в режиме группового искания. Метод КЛИГС

Комбинаторный метод Якобеуса, рассмотренный на примере двухзвеньевых схем, без существенных усложнений может быть использован для расчета трехзвеньевых схем. Некоторые четырехзвеньевые схемы также можно проанализировать комбинаторным методом, принимая простейшие предположения о распределениях вероятностей занятия промежуточных линий в отдельных звеньях. Использование комбинаторного метода для схем с большим числом звеньев (пять и более) в настоящем его виде затруднительно.

Метод эффективной доступности приспособлен для расчета двухзвеньевых схем в режиме группового или свободного искания, а также трехзвеньевых схем в режиме индивидуального искания. Однако обобщение этого метода возможно для схем с большим числом звеньев. Если вместо эффективной доступности использовать среднюю доступность, то анализ многозвеньевых коммутационных схем дополнительно упрощается.

Таким образом, комбинаторный метод и метод эффективной доступности в основном обеспечивают расчеты числа соединительных устройств, включаемых в выходы двухзвеньевых коммутационных схем. При проектировании отечественных АТС координатной системы (АТСК и АТСКУ) определение объема коммутационного оборудования сводится к анализу двухзвеньевых схем, поэтому данные методы позволяют обеспечить нужды проектирования таких АТС.

Структура квазиэлектронных АТС такова, что для их анализа и проектирования необходимо рассматривать коммутационные схемы с четырьмя, шестью и более звеньями соединений. Из-за сложности расчета схем с большим числом звеньев, связанной в основном со сложностью их структуры, до последнего времени, за исключением метода вероятностных графов, не было даже приближенных инженерных методов анализа многозвеньевых схем. Использование понятия эффективной доступности и методов статистического моделирования позволило А. Лотце разработать приближенные методы расчета многозвеньевых схем в режиме группового искания (метод КЛИГС) и в режиме индивидуального искания (метод ППЛ), а также предложить метод оптимизации коммутационных схем по числу точек коммутации.

Метод КЛИГС получил сокращенное название от английских слов, означающих «расчет звеньевых систем группового искания». Метод основывается на понятиях средней доступности (свободный веер) d _cp, средней недоступности (занятый веер) ` d _cp, максимальной доступности (максимальный веер) d_max коммутаторов последнего звена от любого свободного входа первого звена. С помощью этих понятий определяется эффективная доступность d _э, значение которой позволяет вычислить вероятность потерь, пользуясь модифицированной формулой Пальма – Якобеуса. Используем следующие обозначения:

т_i – число выходов коммутатора i -ro звена; k_i – число коммутаторов i -ro звена; s – число звеньев;

q_r – число выходов из одного коммутатора последнего звена в направлении r; u _r – число линий в пучке r -го направления; М – общее число выходов схемы;

u _{i, i+ 1}– общее число промежуточных линий между соседними звеньями;

s_вx=u_1,2/ N – коэффициент расширения на входе; s_вых= M /u_{s-1, s}– коэффициент концентрации на выходе. Тогда

где y_i – обслуженная нагрузка коммутатора i-ro звена.

На соотношение (9.38) налагается следующее ограничение:

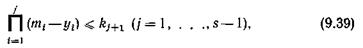
которое означает, что средняя доступность коммутаторов любого звена от любого свободного входа не может превышать числа коммутаторов в соответствующем звене.

Величина d _cр равна среднему числу коммутаторов последнего звена, доступных от любого свободного входа в первом звене через свободные промежуточные линии между звеньями. Максимальная доступность определяется выражением

и равна максимальному числу коммутаторов последнего звена, доступных от любого свободного входа первого звена. Она равна средней доступности при нулевой нагрузке и ограничена соотношением d_max £ k_s. Средняя недоступность определяется соотношением

и соответствует среднему числу недоступных коммутаторов последнего звена, равному разности между количеством коммутаторов, доступных при нулевой нагрузке и заданной обслуженной нагрузке.

В рассматриваемом методе эффективная доступность определяется как сумма двух слагаемых:

Первое из этих слагаемых является функцией d _cp, определяется соотношением

и представляет собой среднее число выходов рассматриваемого r -го направления, которые могут заниматься через промежуточные линии, образующие среднюю доступность (свободный веер). Второе слагаемое эффективной доступности задается выражением

где y _{o r} – обслуженная нагрузка r -го направления; у _o – общая обслуженная нагрузка.

Произведение первых двух сомножителей в правой части (9.44) выражает число выходов рассматриваемого направления, находящихся в недоступных коммутаторах последнего звена. Умножением на третий множитель y _{o r} / u _r получаем среднее число занятых выходов рассматриваемого направления, которые находятся в недоступных коммутаторах. Четвертый множитель представляет собой отношение среднего числа свободных входов в последнее звено к общему числу выходов последнего звена и является коэффициентом, учитывающим степень концентрации в последнем звене.

После определения эффективной доступности по (9.42) считают, что вероятность потерь в многозвеньевой схеме равна вероятности потерь в однозвеньевой схеме с доступностью, равной эффективной доступности. Для расчета вероятности потерь р применяется модифицированная формула Пальма – Якобеуса (см. гл. 8)

В числителе (9.45) стоит функция Эрланга, выражающая потери в полнодоступном пучке, содержащем u _r линий, на который поступает некоторая фиктивная нагрузка у _{ф r} , в знаменателе – функция Эрланга, выражающая потери в полнодоступном пучке из u _r – d _э линий при той же нагрузке. Фиктивная нагрузка у _{ф r} определяется из соотношения

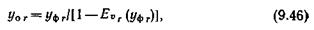
а фактически поступающая на направление нагрузка у_r определится затем из соотношения

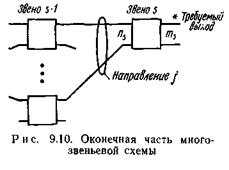Точность рассмотренного метода проверена статистическим моделированием. Метод позволяет определить вероятность потерь в многозвеньевых схемах, в которых число промежуточных линий между всеми звеньями одинаково, а s_вх³1 и s_вых£1, при этом схемы могут иметь как веерную, так и связанную структуры неделимого или блочного типа.

При использовании s -звеньевых блокирующих коммутационных схем в режиме индивидуального искания пучок, состоящий из n_s промежуточных линий между предпоследним и последним звеньями, входящих в тот коммутатор последнего звена, в который включен требуемый выход, можно рассматривать (рис. 9.10) как некоторое направление j коммутационной схемы с числом звеньев на единицу меньше (схемы с s –1 звеном). В этом случае работа s-звенье-вой схемы в режиме индивидуального искания эквивалентна работе (s –1)-звеньевой схеме в режиме группового искания. Поэтому методы расчета, применимые в режиме группового искания, могут быть использованы для расчета схем в режиме индивидуального искания. В частности, метод КЛИГС, предложенный А. Лотце для режима группового искания, можно применить для схем, используемых в режиме индивидуального искания. Для многозвеньевых блокирующих схем, работающих в режиме индивидуального искания, разработаны также специальные методы расчета.

9.10. Метод вероятностных графов

Метод основывается на представлении коммутационной схемы в виде графа, конфигурация которого зависит не только от структуры схемы, но и от режима искания, в котором используется схема. Переход от коммутационной схемы практически любой сложности к графу не представляет принципиальных трудностей. Граф, представляющий собой картину всевозможных путей между заданным входом схемы и заданным выходом (или одним из выходов заданной группы), может принадлежать к классу параллельно-последовательных графов или к классу непараллельно-последовательных (мостиковых) графов.

Дальнейшая процедура метода вероятностных графов заключается в том, чтобы записать функцию для вероятности потерь при установлении соединений в рассматриваемом графе между его входными и выходными полюсами, аргументами которой являются вероятности занятости отдельных дуг графа. Для определения вероятностей занятости дуг обычно используют значение средней интенсивности нагрузки, обслуженной каждой из них. Записанная таким образом функция позволяет определить вероятности потерь или оптимизировать структуру по числу точек коммутации или другим показателям.

Для того чтобы уяснить соответствие между коммутационной схемой и представляющим ее графом и способ перехода от схемы к графу, рассмотрим графы отдельных типовых коммутационных схем. Трехзвеньевая коммутационная схема, приведенная на рис. 9.4 б, в зависимости от режима искания будет соответствовать одному из вероятностных графов, изображенных на рис. 9.11. При построении этих графов считаем, что коммутационная схема – односвязная (одна промежуточная линия между каждой парой коммутаторов соседних звеньев), а структурные параметры схемы удовлетворяют следующим соотношениям: k ₂ =m ₁; п ₂= k ₁; k ₃ =m ₂; n ₃= k ₂ =m ₁.

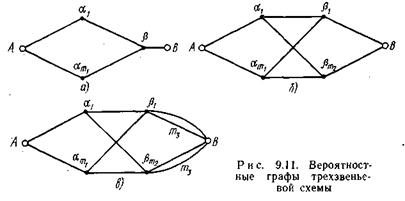На рис. 9.11 а приведен вероятностный граф трехзвеньевой коммутационной схемы, используемой в режиме индивидуального искания (определенный вход должен быть подключен к точно указанному выходу). Дуги A a _i, соединяющие входной полюс А ивершины a _i, изображают промежуточные линии между звеньями 1 и 2, дуги a _i b, соединяющие вершины a _i с вершиной b, изображают промежуточные линии между звеньями 2 и 3, а дуга b В, соединяющая вершину b с выходным полюсом В, изображает выход коммутационной схемы, к которому должен быть подключен заданный вход при использовании схемы в режиме индивидуального искания (режим И).

Дата добавления: 2014-11-29