Определение вероятностей состояния полнодоступного пучка. 9 страница

При такой конфигурации графа совокупность всех путей награфе, содержащих дуги, лежащие между входным и выходнымполюсами (полюса A и В), является совокупностью всех возможных путей установления соединения анализируемой коммутационной схемы в рассматриваемом режиме искания.

На рис. 9.11 б приведен вероятностный граф той же трехзвенье-вой коммутационной схемы, используемой в режиме группового искания (определенный вход должен быть подключен к одному из свободных выходов в заданной группе – направлении). Граф изображен для случая, когда рассматриваемая группа выходов (направление) содержит только по одному выходу в каждом коммутаторе третьего звена.

На этом рисунке, как и на предыдущем, дуги A a _i изображают промежуточные линии между звеньями 1 и 2, дуги a _i b _i – промежуточные линии между звеньями 2 и 3, а дуги b _jB – выходы рассматриваемого направления, к одному из которых должен быть подключен заданный вход в режиме группового искания (режиме Г).

Рассматриваемый граф, как и в предыдущем случае (рис. 9.11 а), изображает совокупность всех возможных путей установления соединения в анализируемой схеме (см. рис. 9.4 б) в режиме группового искания.

На рис. 9.11 б приведен вероятностный граф трехзвеньевой коммутационной схемы в режиме свободного искания (режим С), в котором определенный вход должен быть подключен к одному из свободных выходов всей схемы. Этот граф отличается от предыдущего только тем, что между каждой вершиной b _i и полюсом В имеется не одна, а m ₃ дуг, изображающих тз выходов из каждого коммутатора третьего звена.

Если в режиме Г для рассматриваемого направления в каждом из коммутаторов третьего звена используется q выходов, то структура графа будет такой же, как показано на рис. 9.11 в, a между вершинами b _j и полюсом В будет q дуг вместо m ₃.

Приведенные на рис. 9.11 три вероятностных графа трехзвеньевой схемы рис. 9.4 б соответствуют, как указано выше, трем режимам искания. В режиме И трехзвеньевая схема имеет граф параллельно-последовательного типа (тип П), а в режимах Г и С – граф непараллельно-последовательного типа (тип Н).

Рассмотренные принципы построения графов трехзвеньевой коммутационной схемы позволяют построить вероятностный граф для схемы с любым числом звеньев, учитывая закономерность построения, подмеченную в рассмотренных примерах. Увеличение числа звеньев схемы приводит к возрастанию числа звеньев графа, однако принцип построения сохраняется тот же.

Запись функции потерь вида p=f( w_, w₂ ,..., w _i,..., w _s), где p – вероятность потерь, a w _i – вероятность занятости каждой дуги i -ro звена, сводится для графов параллельно-последовательного типа к умножению и суммированию вероятностей w _i,так как предполагается независимость событий, происходящих в различных звеньях графа (коммутационной схемы). При этом в случае параллельного включения нескольких дуг, образующих некоторую общую ветвь, для получения вероятности занятости всей ветви вычисляют произведение вероятностей занятости отдельных дуг. Если ветвь образуется последовательным включением (цепочкой) дуг, то вероятность занятости всей ветви определяется как дополнительная вероятность к вероятности свободности всей ветви, а вероятность свободности всей ветви, в свою очередь, определяется как произведение вероятностей свободности отдельных последовательно включенных дуг.

Обозначим вероятность занятости дуг для параллельно-последовательного графа, приведенного на рис. 9.11 a, соответственно w₁(для дуг A a _i), w ₂ (для дуг a _i b) и w₃(для дуги b B), а вероятности свободности этих же дуг через q ₁ = 1–w₁, q ₁ = 1 – w ₂ и q ₃=1–w₃. Тогда вероятность того, что один из путей между полюсом А и вершиной b, состоящий из двух дуг, будет свободен, составит 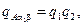а вероятность занятости этого пути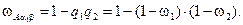

Вероятность занятости всех т ₁путей между полюсом А и вершиной р будет равна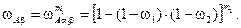

Для того чтобы подсчитать вероятность потерь р, равную вероятности занятости всех возможных путей между полюсами А и В ( w _ab), определим вероятность свободности хотя бы одного пути между полюсами А и В какпроизведение вероятностей свободности ветви Ab и дуги b B:

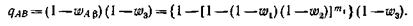
В свою очередь, вероятность потерь будет равна

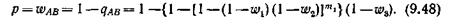
Таким образом, функция вероятности потерь для графа по рис. 9.11 а будет определяться (9.48). Следовательно, для вероятности потерь трехзвеньевой схемы (см. рис. 9.4 б) в режиме индивидуального искания по методу вероятностных графов также будет справедлива ф-ла (9.48).

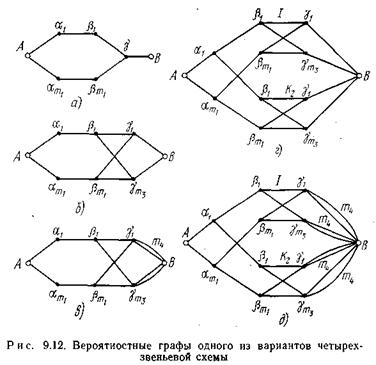Во многих случаях графы коммутационных схем относятся к классу непараллельно-последовательных. Так, коммутационной схеме, приведенной на рис. 9.5 б, в зависимости от режима искания соответствует один из графов рис. 9.12. На рис. 9.12 а приведен граф для режима индивидуального искания. В режиме группового искания схема рис. 9.5 б будет иметь один из графов, приведенных на рис. 9.12 б, в, г. Первый из этих графов соответствует случаю, когда к выходам одной группы относятся по одному выходу из каждого коммутатора только одного двухзвеньевого блока. Второй граф соответствует случаю, когда все выходы этого двухзвеньевого блока образуют искомую группу выходов. Третий граф справедлив для случая, когда группа выходов образуется путем использования по одному из выходов от каждого коммутатора всей схемы.

В режиме свободного искания рассматриваемая схема будет соответствовать графу на рис. 9.12 д

Как видно из рис. 9.12, все графы, за исключением первого (рис. 9.12а), принадлежат к классу непараллельно-последовательных графов и в их структуре существенную роль играет простейший непараллельно-последовательный (мостиковый) граф, показанный на рис. 9.11 б. Формула для вычисления вероятности потерь такого мостикого графа будет иметь вид

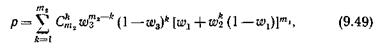
где w₁ w₂иw₃– вероятности занятости дуг графа на рис. 9.11 б.

Во многих случаях вычисление вероятности потерь для более сложных непараллельно-последовательных графов сводится к приемам, применимым для параллельно-последовательных графов в сочетании с ф-лой (9.49). В тех случаях, когда вычисление потерь для непараллельно-последовательного графа слишком громоздко, можно пользоваться методом оценочных графов.

Для рассматриваемого графа из класса непараллельно-последовательных схем подбирают два параллельно-последовательных графа, причем таким образом, чтобы вероятность потерь для одного из них была оценкой сверху вероятности потерь в рассматриваемом графе, а вероятность потерь для другого графа – оценкой снизу. Тогда искомая вероятность потерь для исследуемого графа будет заключена между двумя значениями потерь, выражения для которых легко записать.

Получение оценочных графов осуществляется с помощью некоторых операций. Граф для получения оценки по потерям сверху получают путем использования операций выбрасывания отдельных дуг и разделения одной вершины на две или несколько, что приводит к заведомому увеличению потерь. Для получения графа, пригодного для оценки вероятности потерь снизу, используются противоположные операции добавления дуг и объединения вершин, которые приводят к уменьшению потерь.

9.11. Оптимизация многозвеньевых коммутационных схем

При разработке многозвеньевых схем с блокировками новые схемы получают по аналогии с уже известными, используя опыт и интуицию проектировщика. В этом случае обычно рассматривается несколько классов коммутационных схем. В пределах каждого из классов проводится возможная в рамках имеющихся методов оптимизация с последующим сопоставлением лучших вариантов каждого класса и выбором требуемой схемы. В качестве критерия при выборе структуры коммутационных схем в большинстве случаев пользуются числом точек коммутации.

Иногда при проектировании блокирующих коммутационных схем используют методику синтеза неблокирующих коммутационных схем. В таком случае по заданным характеристикам блокирующей схемы выбирают неблокирующую схему с оптимальными структурными параметрами, которая имеет большее число точек коммутации, чем требуемая блокирующая схема. Далее путем устранения некоторых соединительных путей получают блокирующую схему с заданной нормой блокировок при заданной нагрузке на один вход, которая во многих случаях близка к оптимальной.

Естественно, что при проектировании коммутационных схем существенное значение имеют методы оптимизации и особенно такие, которые позволяют выбирать оптимальную схему по заданному показателю в пределах широкого класса структур. В работах Лотце разработан метод оптимизации многозвеньевых коммутационных схем по числу точек коммутации с помощью простых аналитических выражений. Полученные формулы дают возможность определить структурные параметры схемы и удельную нагрузку на одну промежуточную линию.

Указанный метод оптимизации справедлив для многозвеньевых схем, не имеющих существенной концентрации в промежуточных звеньях, за исключением последнего. В первом звене целесообразно использовать расширение. Метод не требует применения каких-либо приближенных формул для определения вероятности потерь. Используются лишь две характеристики: нагрузка, обслуженная одним входом первого звена (a_i), и прозрачность схемы (Т).

Если суммарное число выходов последнего звена остается постоянным, то число исходящих направлений, на которое разбиваются выходы, не влияет на результаты оптимизации. Оптимальные структурные параметры могут быть определены не только для оптимального, но и для любого другого числа звеньев.

Основные соотношения, используемые при оптимизации схем по этому методу, получаются из анализа выражения для числа точек коммутации С на один эрланг нагрузки.

Для многозвеньевых коммутационных схем с s звеньями при любой обслуженной нагрузке, отличной от нуля, это выражение имеет вид

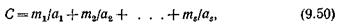
где m_i – число выходов из коммутаторов i -звена; а_i – нагрузка, обслуженная одним входом i -звена.

Далее используется понятие прозрачности коммутационной схемы, под которой понимают среднее количество свободных путей в схеме между заданным входом и всеми М выходами схемы.

Значение прозрачности Т определяется выражением

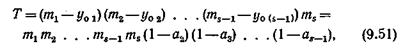
где y _{o i} – нагрузка, обслуженная m_i выходами одного коммутатора i -звена; a_i – нагрузка, обслуженная одним входом i -звена.

Если из (9.51) выразить т ₁и подставить в (9.50), то получим следующее соотношение для С:

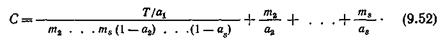
При синтезе блокирующих коммутационных схем величина нагрузки а ₁на один вход схемы считается заданной, поэтому оптимизация структуры коммутационной схемы по числу точек коммутации заключается в том, чтобы подобрать такие емкости коммутаторов m ₂,..., m_s и такие нагрузки на один вход коммутаторов a ₂ ,..., a_s, при которых число точек коммутации С на один эрланг нагрузки будет минимальным. При этом значение прозрачности Т предполагается постоянным и таким, которое гарантирует требуемые качественные показатели схемы.

Решая систему из 2 (s –1) уравнений, которая получается, если положить равными нулю частные производные по всем аргументам ¶ С/ ¶ т ₂ =...= ¶ C/ ¶ m_s =¶ С/ ¶ а ₂=...=¶ C/ ¶ a_s= 0, получаем следующие основные формулы, используемые для оптимизации структуры:

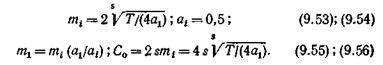
Формулы (9.53) – (9.56) справедливы для i =2, 3,..., s и заданного числа s-звеньев схемы. Число точек коммутации С на один эрланг нагрузки, в том числе и С _o, полученное оптимизацией по m_i и a_i, зависит также от числа s -звеньев схемы.

а минимальное число точек коммутации на один эрланг будет равно

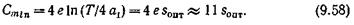
Оптимальное число звеньев схемы из выражения (9.56), при котором число точек коммутации на один эрланг будет минимальным, определяется следующим выражением:

Формулы (9.53) – (9.58) используются для оптимизации блокирующих многозвеньевых коммутационных схем по числу точек коммутации.

В процессе оптимизации считаются заданными общее число N входов схемы, общее число М выходов схемы, нагрузка а ₁на один вход и требуемая величина прозрачности Т. По заданным величинам можно определить оптимальное значение числа звеньев s _опт, а также для s _опт или любого заранее выбранного s подсчитать структурные параметры схемы (m ₁ ,...,m_s) и определить соответствующие нагрузки на входы (a ₁ ,...,a_s) и число точек коммутации на один эрланг (С _oили C_min).

Контрольные вопросы

1. Приведите общее выражение для вероятности потерь в двухзвеньевой односвязной полнодоступной схеме ори использовании комбинаторного метода Якобеуса и укажите, при каких предположениях оно справедливо.

2. Какие распределения используются для аппроксимации вероятностей занятия промежуточных линий и выходов схемы в комбинаторном методе Якобеуса?

3. Пользуясь комбинаторным методом, запишите выражение вероятности потерь в режиме индивидуального искания (фиксированный вход схемы подключается к фиксированному выходу схемы) для трехзвеньевой схемы, приведенной на рис. 9.4, в случае квадратных коммутаторов в первом звене (n ₁ = m ₁).

4. В чем заключается идея комбинаторного метода Якобеуса для расчета двухзвеньевых яеполнодоступных схем?

5. Чему равна минимальная и максимальная доступности двухзвеньевой полнодоступной схемы с параметрами n ₁=10, m ₁=20, q =2?

6. Какова эффективная доступность двухзвеньевой схемы, приведенной на рис. 9.1, если зависимость потерь от доступности является линейной?

7. Какие методы расчета пригодны для коммутационных схем с тремя и более звеньями соединения?

8. Перечислите способы межзвеньевых соединений, используемые в многозвеньевых схемах.

9. Какие методы искания наиболее часто используются в миогозвеньевых схемах?

10. Как определяется эффективная доступность многозвеньевой схемы в соответствии с методом КЛИГС?

11. Каков порядок расчета многозвеньевых коммутационных схем в режиме группового искания по методу КЛИГС?

12. Что такое прозрачность коммутационной схемы?

13. Какова идея оптимизации многозвеньевых коммутационных схем?

14. Каким образом устанавливается однозначное соответствие между коммутационной схемой и графом?

15. Как записывается выражение для вероятности потерь в параллельно-последовательном графе?

16. Приведите формулу для определения вероятности потерь в простейшем графе непараллельно-последовательного типа.

17. Изобразите графы, соответствующие двух-, трех- и четырехзвеньевым схемам в режимах свободного, группового и индивидуального исканий.

18. Как оценить величину вероятности потерь в сложном непараллельно-последовательном графе?

ГЛАВА ДЕСЯТАЯ

Распределение нагрузки и потерь на сетях связи

10.1. Качество обслуживания на автоматически коммутируемых сетях связи

Суммарные потери. Качество обслуживания потоков вызовов рассмотрим на примере автоматических телефонных сетей. В нашей стране создается общегосударственная автоматически коммутируемая телефонная сеть, в состав которой входят междугородная, внутризоновые, городские и сельские телефонные сети. Основной дисциплиной обслуживания потоков вызовов на автоматически коммутируемых телефонных сетях в нашей стране является обслуживание с явными потерями. При этом основной количественной характеристикой качества обслуживания потоков вызовов является математическое ожидание величины потерь из-за отсутствия свободных и исправных соединительных устройств при установлении соединения между двумя телефонными аппаратами.

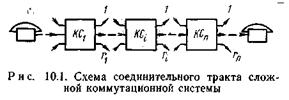
Пусть соединительный тракт содержит п последовательно включенных ступеней искания. Поступающий на i -ю ступень искания поток вызовов делится на r_i потоков в соответствии с числом направлений, организуемых на ступени искания (рис. 10.1). Пусть на каждом направлении i -й ступени искания число соединительных устройств рассчитывается при величине потерь p_i (i =1, 2,......, п). Определим результирующую величину потерь р при установлении соединения между двумя телефонными аппаратами через п ступеней искания.

Исследования сложных коммутационных систем показали, что величина р зависит от величин потерь на отдельных ступенях искания p_i (i =1, 2...., n), числа ступеней искания n, числа направлений r, включаемых в каждую ступень искания, т. е. p=f(p ₁, р ₂,..., p_п, п, r ₁, r ₂,..., r_n). При этом величина потерь р находится в пределах

где 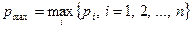– максимальное из значений потерь на ступенях искания сложной коммутационной системы.

Если на входы и выходы любого числа ступеней искания включено только одно направление, то имеет место равенство

В другом предельном случае при r ®¥ процессы обслуживания потоков, поступающих на направления разных ступеней искания, независимы и математическое ожидание величины потерь р при установлении соединения между двумя телефонными аппаратами через n ступеней искания определяется из выражения

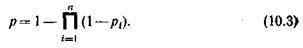
Действительно, вероятность того, что поступающий вызов будет обслужен на первой ступени, равна (1– р ₁ ), на второй ступени– (1– р ₂ ) и т. д., на n -й ступени– (1– р_п). Тогда вероятность того, что поступающий вызов будет обслужен и на первой, и на второй, и т. д., и на n -й ступени искания, равна 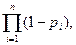а искомая вероятность того, что вызов не будет обслужен хотя бы на одной ступени искания, определится из выражения (10.3).

В реальных коммутационных системах величина r конечна. Так как каждый вызов занимает соединительные устройства нескольких ступеней искания, то состояния этих ступеней не являются независимыми. Кроме того, из-за потерь на ступенях искания меняется характер потока вызовов, поэтому ф-ла (10.3) является приближенной. В большинстве практических случаев р_i £0,01 (i =l, 2,..., n) и без большой погрешности выражение (10.3) можно заменить следующей простой формулой:

так как члены, содержащие произведения, в этом случае пренебрежимо малы. В соответствии с (10.4) результирующие потери равны сумме потерь на всех ступенях искания, поэтому потери р называют суммарными потерями.

Из предыдущих глав известно, что с уменьшением потерь (по-вышением качества обслуживания) увеличивается объем станционных и линейных сооружений, а следовательно, и затраты на построение сети. Емкости пучков линий (каналов) и их протяженность существенно различаются на междугородной, внутризоновых, городских и сельских телефонных сетях. На любой сети затраты на построение отдельных участков соединительного тракта также могут значительно различаться. Для снижения суммарных затрат на построение телефонных сетей нормируется тем большая величина суммарных потерь на сети, чем больше протяженность пучков линий (каналов) и меньше их емкости. По этим соображениям минимальная норма суммарных потерь принята на городских телефонных сетях и большая – на сельских телефонных сетях, на которых преобладают пучки соединительных линий малой емкости. В пределах одной сети суммарные потери распределяются по ступеням искания таким образом, что на более дорогие участки соединительного тракта отводится большая величина потерь.

Нормы потерь при городской телефонной связи. Суммарные потери при установлении соединения между двумя телефонными аппаратами одной ГТС не должны превышать 0,02–0,03; при связи между телефонными аппаратами ГТС и телефонным аппаратом пригородной зоны, на которой приняты нормы потерь ГТС, – 0,04. Величина потерь на участках между входами соседних ступеней ГИ, а также между входами последней ступени ГИ и ЛИ (АИ) не должна превышать 0,005; на участке IГИ–IIГИ узла специальных служб –0,001.

Нормы потерь при сельской телефонной связи. Суммарные потери при установлении соединений между двумя телефонными аппаратами одной СТС не должны превышать 0,035–0,11. Потери при расчете количества соединительных линий на участках оконечная станция (ОС) – центральная станция (ЦС), оконечная станция – узловая станция (УС) не должны превышать 0,02– 0,03; на участке УС–ЦС–0,01. Потери между входами соседних ступеней ГИ, а также между входами последней ступени ГИ и ЛИ (АИ) АТС не должны превышать 0,005; на участке IГИ–IIГИ специальных служб – 0,001.

Нормы потерь при зоновой телефонной связи. Суммарные потери при установлении соединений между двумя телефонными аппаратами разных местных сетей одной зоновой телефонной сети (ЗТС) не должны превышать 0,03–0,125. Нормы потерь на участках соединительного тракта ЗТС приведены в табл. 10.1.

ТАБЛИЦА 10.1

Участок	Нормы потерь на участках соединительного тракта ЗТС
Города, где расположены АМТС	Райцентры	Выделенные города
IГИ– АМТС	0,005	0,01	0,01
АМТС– РАТС (УВСМ)	0,002	–	0,01
АМТС– ЦС	–	0,01	–
Между входами соседних ступеней ГИМ	0,001	0,001	0,001

Нормы потерь при междугородной телефонной связи. Суммарные потери при установлении соединений между двумя телефонными аппаратами ГТС, расположенных в разных зонах семизначной нумерации, не должны превышать 0,1. Количество каналов на одном участке пути последнего выбора должно рассчитываться при величине потерь 0,01. Вероятность потерь в коммутационной системе станций типов АМТС-4, АРМ-20, АМТС-КЭ, УАК-КЭ не должна превышать 0,003; АМТС-2 и АМТС-3 – 0,007. Нормы потерь на участках телефонный аппарат – АМТС и АМТС – телефонный аппарат такие же, как при зоновой телефонной связи.

10.2. Расчет нагрузок на входах и выходах ступеней искания коммутационных узлов

Для каждой ступени искания АТС или узла расчет интенсивности поступающей на входы и выходы нагрузки производится раздельно, так как при этом необходимо учитывать перераспределение потоков нагрузки по направлениям разных ступеней искания, потери сообщения и различие в значениях средней длительности занятия на этих ступенях искания. Расчеты нагрузок по ступеням искания рассмотрим на примере координатных телефонных станций АТСК.

Интенсивность нагрузки, поступающей на ступень абонентского искания. Во входы ступени АИ координатных АТС могут включаться линии от квартирных телефонных аппаратов индивидуального пользования, коллективного пользования или спаренных, телефонных аппаратов народнохозяйственного сектора, таксофонов с интенсивностью удельной исходящей нагрузки менее 0,33 Эрл, соединительные линии от учрежденческих телефонных станций (УТС) малой емкости. Среднее число вызовов и средняя продолжительность разговора у этих источников нагрузки неодинаковы. Интенсивность нагрузки, создаваемой абонентами квартирного сектора, достигает максимального значения в вечерние часы суток, а народнохозяйственного сектора – в утренние часы. По этим причинам для определения максимальной суммарной нагрузки, поступающей от источников разных категорий, расчеты следует проводить как для утреннего, так и для вечернего ЧНН.

Интенсивность исходящей нагрузки, обслуживаемой ступенью АИ в ЧНН, представляет собой сумму интенсивностей нагрузок, поступающих по всем линиям, включенным в ступень:

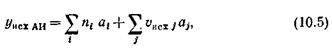
где n_i – число источников i -й категории; а_i – среднее значение интенсивности удельной исходящей нагрузки i -й категории источников в ЧНН; u_{исх j} – число исходящих соединительных линий от j -й УТС; a_j – среднее значение интенсивности нагрузки, поступающей на ступень АИ по одной соединительной линии от j -й УТС 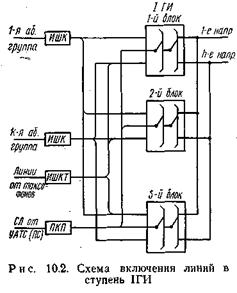в ЧНН. Среднее значение интенсивности удельной исходящей нагрузки источников i -й категории а_i определяется как произведение среднего числа вызовов в единицу времени от одного источника i -й категории ` c<sub>i</sub> на среднюю длительность одного занятия для источника i -й категории ` t_i.

Расчет объема оборудования осуществляется по максимальному из значений интенсивности нагрузки в утренний и вечерний ЧНН.

Интенсивность нагрузок на ступенях группового искания. Нагрузка, поступающая на входы первой ступени группового искания IГИ АТСК, создается абонентскими группами ступени АИ, абонентами УТС и подстанций (ПС), исходящие соединительные линии от которых включены во входы ступени IГИ, а также абонентами таксофонов, линии от которых включены непосредственно во входы IГИ (рис. 10.2). Нагрузка от абонентских групп ступени АИ и от остальных источников, обслуживаемых ступенью IГИ, распределяется по возможности равномерно между всеми блоками ступени.

Средняя величина интенсивности нагрузки, поступающей на входы ступени IГИ, рассчитывается в утренний и вечерний ЧНН по формуле

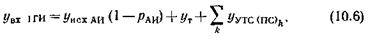
где y _т – интенсивность нагрузки, поступающей от таксофонов; y _{УТС(ПС) k} – интенсивность нагрузки, поступающей от k -й УТС (ПС); р _АИ – потери на ступени АИ.

Нагрузка на выходах ступени IГИ меньше нагрузки, поступающей на ее входы, так как время занятия выхода ступени IГИ меньше времени занятия ее входа на величину, включающую в себя время слушания сигнала ответа станции t _c.oи время набора знаков номера вызываемого абонента – t _н.н. При связи с координатными АТСК регистр принимает все т знаков абонентского номера, а затем устанавливается соединение на ступени IГИ. При связи со станциями декадно-шаговой системы соединение устанавливается после приема т ₁знаков, определяющих код АТС или узла. Среднее время приема регистром знаков набора номера вычисляется с учетом распределения нагрузки между АТС координатной и декадно-шаговой систем по формуле

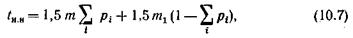
где 1,5 – время набора одного знака номера, с; р_i – доля нагрузки от проектируемой АТС к i -й станции координатной системы. Так как до вычисления нагрузки на выходах ступени IГИ значения p_i могут быть неизвестны, то в первом приближении p_i можно заменить отношением возникающей на i -й АТС координатной системы нагрузки к суммарной возникающей нагрузке на всех АТС проектируемой сети.

Дата добавления: 2014-11-29