Краткие теоретические сведения. Порядок выполнения лабораторной работы

Лабораторная работа № 7

Порядок выполнения лабораторной работы

1. Сформулировать основную и альтернативную гипотезы и проверить с помощью критерия серий однородность приведенной в лабораторной работе 1 выборочной совокупности, используя уровень значимости .

Тема: «Проверка гипотезы о законе распределения (критерии согласия)»

Цель работы: приобретение практических навыков в оценке степени согласованности эмпирических данных и теоретического закона распределения.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе распределения случайной величины. Выдвижение и проверка гипотезы о виде закона распределения генеральной совокупности обычно является завершающим этапом обработки одномерной выборки. На практике для выдвижения такой гипотезы предварительно производят построение гистограммы (см. лаб.раб. № 1), делают предположение о законе распределения и оценивают параметры (см. лаб. раб. № 3).

Для проверки гипотезы о законе распределении генеральной совокупности применяются критерии Колмогорова, Пирсона, Смирнова и т.п. Все эти критерии основываются на сравнении эмпирических (полученных опытным путем) и теоретических (вычисленных в предположении теоретического закона распределения генеральной совокупности) частот или частостей. Критерии согласия позволяют определить характер расхождений между предполагаемым теоретическим и статистическим распределением: связаны ли расхождения со случайными факторами (ограниченное число наблюдений, n) или они существенны и связаны с тем, что подобранная кривая плохо выравнивает статистическое распределение.

Нулевая гипотеза 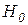состоит в том, что случайная величина X подчинена некоторому определенному закону распределения. Для проверки этой гипотезы выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения. Случайная величина U выбирается таким образом, чтобы при достаточно больших объемах выборки n был известен закон ее распределения и он практически не зависел от закона распределения случайной величины X.

Зная закон распределения случайной величины U, можно посчитать вероятность того, что она не меньше некоторого фактически наблюденного значения: . Если эта вероятность мала, то гипотезу 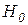следует отвергнуть, как малоправдоподобную. Если эта вероятность – велика, то говорят что экспериментальные данные не противоречат гипотезе 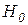. Малая вероятность означает, что за счет чисто случайных расхождений различия между теоретическим и эмпирическим распределением не могут быть объяснены.

Критерий Пирсона (“хи”-квадрат)

В качестве меры расхождения между предполагаемым теоретическим и статистическим распределениями принимается величина, равная взвешенной сумме квадратов отклонений между теоретической вероятностью, рассчитанной по предполагаемому закону (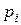), и статистической вероятностью ().

Алгоритм применения критерия Пирсона:

1. Исходя из известных значений эмпирических частот попадания в i-тый интервал, выдвигают нулевую гипотезу о предполагаемом законе распределения случайной величины X и находят его параметры.

2. Определяют теоретические частоты , соответствующие опытным частотам. Здесь 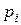- теоретическая вероятность попадания в i- тый интервал:

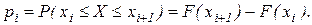
Если среди опытных частот имеются малочисленные, то их необходимо объединить с соседними. Число интервалов после объединения должно быть не менее 4.

3. Определяется мера расхождения между теоретическими и эмпирическими частотами:

4. Определяют число степеней свободы , где k - количество интервалов, s - число параметров предполагаемого теоретического распределения.

5. На заданном уровне значимости и с рассчитанным числом степеней свободы по таблице распределения находят критическое значение значение .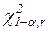

6. Если – принимается нулевая гипотеза (теоретический закон распределения не противоречит эмпирическим данным). Если – нулевую гипотезу отвергают.

Замечание 1. Для объективного принятия решения объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант, малочисленные группы следует объединить в одну, суммируя частоты.

Дата добавления: 2014-11-29