Гипотезы о значении параметра биномиального распределения

Краткие теоретические сведения

Лабораторная работа № 8

Порядок выполнения лабораторной работы

1. Проверить согласованность эмпирического и теоретического (полученных в пп. 2 и 3 лабораторной работы № 3) законов распределения с помощью критериев Пирсона () и Колмогорова. Использовать уровень значимости .

2. Построить гистограммы отклонений.

3. Проанализировать и сопоставить результаты.

Тема: «Проверка гипотезы о параметре биноминального распределения. Гипотезы об ожидаемых числах»

Цель работы: приобретение практических навыков в оценке степени согласованности эмпирических данных и предполагаемого биномиального закона распределения, а также фактических и ожидаемых показателей.

При проверке гипотез о значении параметра биномиального распределения рассматривают задачи следующих видов:

- сравнение вероятности «успеха» p в одном испытании с заданным p₀;

- сравнение вероятностей «успеха» в двух сериях испытаний;

- сравнение вероятностей «успеха» в нескольких сериях испытаний.

Нулевые гипотезы для этих видов задач имеют соответствующий вид

,

,

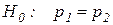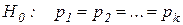
1. Задачи первого типа () возникают, когда при достаточно большом числе n независимых испытаний, имеются основания предполагать, что неизвестная вероятность равна гипотетическому значению.

Пусть в n испытаниях по схеме Бернулли успех произошел m раз. В качестве статистики критерия выбирают относительную частоту p*=m/n. При больших значениях n (n>50) и при выполнении условий mp*>5, n(1-p*)>5 распределение случайной величины p* с достаточной для практических расчетов точностью аппроксимируется нормальным распределением . Отсюда следует, что если гипотеза верна, то статистика

имеет распределение, близкое к нормальному распределению 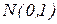. Область принятия основной гипотезы на уровне значимости определяется неравенствами

Двусторонний критерий:

Правосторонний критерий: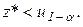

Левосторонний критерий: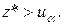

В противном случае гипотеза отклоняется.

2. Задачи второго типа (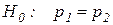) проверяют совпадение параметров двух биномиально распределенных совокупностей. Пусть некоторое событие А в серии из испытаний появилось 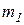раз, а в серии из испытаний появилось 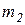раз. Относительная частота появления события А в первой совокупности: . Аналогично .

Проверяется гипотеза о равенстве появления события А в обеих сериях испытаний 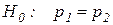. Поскольку вероятности оцениваются по относительным частотам, задачу можно сформулировать так: значимо или незначимо различаются относительные частоты.

Статистика критерия

где

- оценка р.

Если верна нулевая гипотеза, то статистика критерия z имеет распределение, близкое к стандартному нормальному закону: z® N(0,1).

Дополнительное условие:

Область принятия основной гипотезы на уровне значимости определяется неравенствами

Двусторонний критерий:

Правосторонний критерий: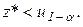

Левосторонний критерий: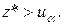

В противном случае гипотеза отклоняется.

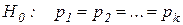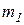3. Задачи третьего типа () проверяют совпадение параметров биномиально распределенных совокупностей числом больше двух. Пусть некоторое событие А в серии из испытаний появилось раз, в серии из испытаний появилось 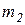раз, …, в серии из 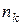испытаний событие А появилось раз. Относительная частота появления события А в соответствующих совокупностях: , , …,

Проверяется гипотеза о равенстве генеральных долей 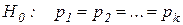. Доказано, что при справедливости нулевой гипотезы и при статистика критерия

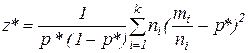
имеет распределение с k-1 степенями свободы. В В качестве неизвестного значения р* берут наилучшую оценку для p, равную выборочной доле признака, если все k выборок смешать в одну:

.

Нулевая гипотеза отвергается, если 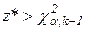, где - критическое значение критерия, определяемое на уровне значимости при числе степеней свободы k-1.

Гипотезы об ожидаемых числах

Пусть по результатам наблюдений получено некоторое множество значений Ф*_i -фактических показателей. При этом вводятся некоторые значения Ф_i - ожидаемые показатели.

Гипотеза Н₀: наблюдаемые показатели совпадают с ожидаемыми (расхождения случайны, связаны с ограниченностью наблюдений).

Доказано, что если Н₀ - истина, то статистика критерия

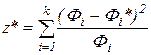
имеет распределение χ² с числом степеней свободы

ν=(s-1)(r-1),

где s – число строк,

r – число столбцов.

Н₀ принимается, если .

Дополнительное условие: метод применим, если Ф_i ≥5, иначе нужно объединить данные (k уменьшится).

Используется при проверке гипотез о независимости двух факторов, при проверке гипотезы о функции плотности распределения.

Пример 1. В течение месяца завод поставил предприятию 200 корпусов, из которых 3 оказались дефектными. В следующем месяце было изготовлено 850 корпусов, из которых 7 оказались дефектными. Изменилась ли доля дефектных корпусов в поставках завода? α=0,01

Нулевая гипотеза H0: p1=p2.

Альтернативная H1:p1≠p2

n1= 200 m1=3

n2= 850 m1=7

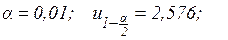
Критерий: 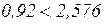, основная гипотеза принимается, доли дефектных корпусов за первый и второй месяц не изменились.

Пример 2. В соответствии со стандартом содержание активного вещества в продукции должно составлять 10%. Выборочная контрольная проверка 100 проб показала содержание активного вещества 15%. На уровне значимости α=0,05 выяснить, должна ли продукция быть забракованной?

Нулевая гипотеза H0: p=p₀=0,10.

Альтернативная H1: p≠p₀=0,10.

Критерий: 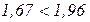, основная гипотеза принимается, продукция не должна быть забракованной.

Контрольные вопросы

1. Критерий проверки гипотезы о сравнении параметра биномиального распределения с номиналом.

2. Критерий проверки гипотезы о сопоставлении двух вероятностей биномиальных распределений.

3. Критерий проверки гипотезы о сопоставлении более чем двух вероятностей биномиальных распределений.

Дата добавления: 2014-11-29