
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристика отдельных процессов. Результаты и их обсуждение
|
|
|
|
Замечания о сходимости итерационного процесса
Исходные уравнения нелинейны. Их линеаризация осуществляется сносом коэффициентов, содержащих значения искомой функции на предыдущий итерационный слой. Далее осуществляются как локальные, так и глобальные итерации. Сходимость итерационного процесса обеспечивается тем, что при реализации прогонок вдоль координатных линий мы стремимся обеспечить диагональное преобладание (хорошую обусловленность метода прогонки). В результате всегда выполняется критерий Скарбороу:
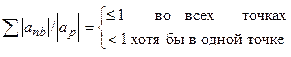 , (23)
, (23)
где 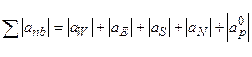 [см. (9)].
[см. (9)].
Из (9) следует, что для того, чтобы выполнялось правило положительной определенности коэффициентов необходимо, чтобы сеточное число Рейнольдса, определенное по поперечной компоненте скорости и шагу по радиальной координате, было меньше 2. Это ограничение не является слишком жестким, т.к. в рамках рассматриваемого класса задач величина V значительно меньше U, абольшие градиенты по r требуют использования мелкого шага по поперечной координате.
Рассмотрим закрученное ламинарное течение несжимаемой жидкости в круглой трубе постоянного сечения. Жидкость на входе в трубу имеет неизменную по сечению осевую скорость, нулевую радиальную и окружную - изменяющуюся по линейному закону (от нуля на оси до максимума у стенки). Как принято говорить, в таких случаях поток на входе в трубу закручен по закону твердого тела. Из-за наличия разности температур входящего в канал потока и стенки трубы течение не является изотермическим. При симметричных граничных условиях для скорости и температуры получающиеся стационарные распределения должны быть осесимметричными.
Представленные рисунками 2-5 графические иллюстрации получены при следующих значениях исходных параметров: 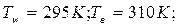 Pr=6,1;
Pr=6,1;  =1 атм; Ro=0¸10;
=1 атм; Ro=0¸10; 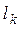 =0,084 м; Re=10¸1600; D =0,007 м.
=0,084 м; Re=10¸1600; D =0,007 м.
На рис.2 приведены распределения относительной скорости на оси трубы ( ) по длине канала в зависимости от безразмерного расстояния X = x /(R ×Re) (Re=
) по длине канала в зависимости от безразмерного расстояния X = x /(R ×Re) (Re=  ), отвечающие различным значениям параметра закрутки Ro=W R /
), отвечающие различным значениям параметра закрутки Ro=W R / 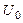 (критерия Россби). Здесь
(критерия Россби). Здесь  - скорости на оси трубы и входе в канал соответственно; R - радиус трубы; n- вязкость жидкости; W r - окружная скорость во входном сечении; x, r - цилиндрические координаты. Значки n - экспериментальные данные В. Пфеннингера, представляющие осевую скорость на начальном участке трубы в прямоточном движении. Пунктир: линии 2, 3 - численное решение Ершова; 4 - приближенное аналитическое решение М.А. Гольдштика (Ro=10,
- скорости на оси трубы и входе в канал соответственно; R - радиус трубы; n- вязкость жидкости; W r - окружная скорость во входном сечении; x, r - цилиндрические координаты. Значки n - экспериментальные данные В. Пфеннингера, представляющие осевую скорость на начальном участке трубы в прямоточном движении. Пунктир: линии 2, 3 - численное решение Ершова; 4 - приближенное аналитическое решение М.А. Гольдштика (Ro=10, 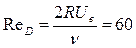 ). Сплошная линия - расчет, полученный на основе предложенной численной модели при следующих значениях определяющих параметров: 1 - Ro=0, 2 - 4, 3 - 5, Re D =160; 4 - Ro=10,
). Сплошная линия - расчет, полученный на основе предложенной численной модели при следующих значениях определяющих параметров: 1 - Ro=0, 2 - 4, 3 - 5, Re D =160; 4 - Ro=10, 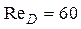 .
.
Из рисунка видно, что при Ro>4 появляется зона возвратных движений. С увеличением Ro зона возвратов существенно увеличивается, а точка минимального значения скорости смещается вниз по течению. На рис.3 представлена кривая обратных токов, полученная расчетным образом (сплошная линия) и по приближенному аналитическому решению М.А.Гольдштика (пунктир). Здесь X=x /(R ×Re). График позволяет оценить размер зоны, где скорость на оси симметрии имеет противоположное основному потоку направление.
На рис.4 показаны зависимости коэффициента трения 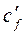 = cf Red от приведенной длины X3=x/(h×Red). Здесь cf =2tw/(r в
= cf Red от приведенной длины X3=x/(h×Red). Здесь cf =2tw/(r в 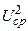 ),
), 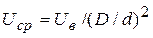 , tw- напряжение трения на стенке, r в - характерная плотность среды, d - диаметр входного сечения, D =2 R - диаметр камеры, h =(D-d)/2 - высота уступа, Uв - средняя скорость во входном сечении; Red= Uв × d /n - число Рейнольдса, H = h/d - коэффициент расширения потока,
, tw- напряжение трения на стенке, r в - характерная плотность среды, d - диаметр входного сечения, D =2 R - диаметр камеры, h =(D-d)/2 - высота уступа, Uв - средняя скорость во входном сечении; Red= Uв × d /n - число Рейнольдса, H = h/d - коэффициент расширения потока,  - параметр закрутки (m = 0. 41). Сплошные линии (1-5) - расчет по предлагаемой модели; значки 1 - ¡, 2 - n, 3 -t, 4 - ¨, 5 - h- результаты измерений в круглой трубе. Кривые 1,2 отвечают соответственно значениям: Red=10 и 250; (H =0,5). Эти расчеты выполнены в условиях экспериментов Дж.П. Льюиса, Р.Х. Плетчера. Кривые 3-5 соответствуют значениям S=0,94; S=0,41; S=0 (Red=100, H =4,5) соответственно.
- параметр закрутки (m = 0. 41). Сплошные линии (1-5) - расчет по предлагаемой модели; значки 1 - ¡, 2 - n, 3 -t, 4 - ¨, 5 - h- результаты измерений в круглой трубе. Кривые 1,2 отвечают соответственно значениям: Red=10 и 250; (H =0,5). Эти расчеты выполнены в условиях экспериментов Дж.П. Льюиса, Р.Х. Плетчера. Кривые 3-5 соответствуют значениям S=0,94; S=0,41; S=0 (Red=100, H =4,5) соответственно.
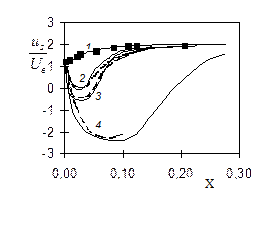 Рис. 2 Рис. 2
| 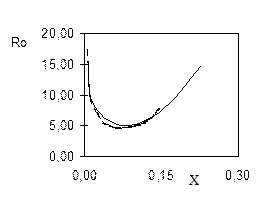 Рис. 3
Рис. 3
|
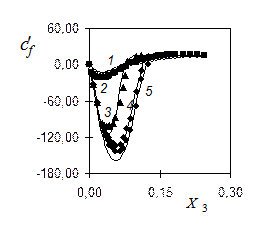 Рис. 4
Рис. 4
|
 Рис. 5
Рис. 5
|
 Рис. 6.
Рис. 6.
|
 Рис. 7.
Рис. 7.
|
Рис. 2. Распределение относительной скорости на оси трубы 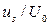 в зависимости от приведенной длины X=x/(R×Re) при различных значениях параметра Россби Ro. Здесь линии – расчет, значки – эксперимент В. Пфеннингера. Сплошные линии – наш расчет для условий: 1 - Ro=0, 2-4, 3-5, ReD=160; 4 - Ro=10, ReD =60. Пунктир: линии 2, 3 – численное решение А.И. Ершова, 4- решение М.А. Гольдштика.
в зависимости от приведенной длины X=x/(R×Re) при различных значениях параметра Россби Ro. Здесь линии – расчет, значки – эксперимент В. Пфеннингера. Сплошные линии – наш расчет для условий: 1 - Ro=0, 2-4, 3-5, ReD=160; 4 - Ro=10, ReD =60. Пунктир: линии 2, 3 – численное решение А.И. Ершова, 4- решение М.А. Гольдштика.
Рис. 3. Кривая обратных токов в зависимости от изменения чисел Россби (Ro) и приведенной длины X. Здесь сплошная линия – расчет по настоящей модели, пунктир – данные расчета М.А. Гольдштика.
Рис. 4. Изменение коэффициента трения 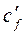 =cfRed от приведенной длины X3=x/(h×Red). Сплошные линии – расчет по данной модели, значки – эксперимент Дж.П. Льюиса. Здесь 1 – Red=10, H=0,5 (m); 2 – Red=250, H=0,5 (n) (прямоточное течение); 3 – S=0,94 (t); 4 – 0,41 (u); 5 – 0 (l) (для Red=100, H=0,5).
=cfRed от приведенной длины X3=x/(h×Red). Сплошные линии – расчет по данной модели, значки – эксперимент Дж.П. Льюиса. Здесь 1 – Red=10, H=0,5 (m); 2 – Red=250, H=0,5 (n) (прямоточное течение); 3 – S=0,94 (t); 4 – 0,41 (u); 5 – 0 (l) (для Red=100, H=0,5).
Рис. 5. Развитие безразмерной осевой компонента вектора скорости по длине канала при Red=10 для течения без уступа. Слева направо соответственно сечения: х/D=0,23; 0,3; 0,38; 0,6; 0,9 (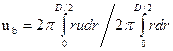 ).
).
Рис. 6. Развитие безразмерной осевой компонента вектора скорости по длине канала при Red=10 с уступом 2h/D=0,71. Сечения по длине трубы, аналогичны рис.5.
Рис. 7. Развитие безразмерной осевой компонента вектора скорости по длине канала при Red=30 с уступом 2h/D=0,71. Сечения по длине трубе (см. рис.5).
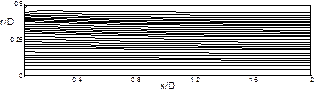
| 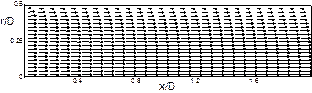
|
| 2h/D=0,1 | |
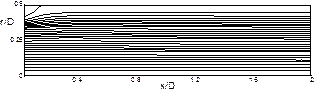
| 
|
| 2h/D=0,2 | |
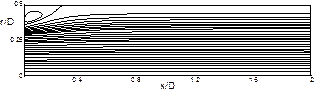
| 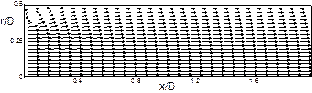
|
| 2h/D=0,3 | |

| 
|
| 2h/D=0,4 | |

| 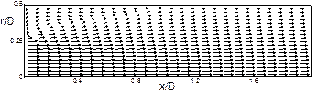
|
| 2h/D=0,5 | |
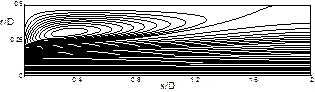
| 
|
| 2h/D=0,6 |
Рис. 8. Серия типичных линий тока и векторных полей скорости при обтекании уступов различной высоты для Red=100. Здесь x,r – переменные координаты цилиндрической системы координат; h – высота уступа; D – диаметр трубы на выходе; Red=ρu0d/µ (d=D-2h).
Отдельные результаты расчета течений в трубах переменного поперечного сечения с привлечением метода контрольного объема и Simple-алгоритма С. Патанкара приведены на рис.5-8. Заметим, что получаемые по ходу аппроксимации СЛАУ с трёхдиагональными матрицами коэффициентов для приближенных значений компонент вектора скорости и поправки давления решались методом прогонки. Расчеты показывают(см. рис. 2-5)), что оба алгоритма достаточно корректно предсказывают границы особых рециркуляционных зон и дают удовлетворительное количественное согласие с данными опытов
Заметим также, что описанная численная процедура имеет преимущество в быстродействии в сравнении с алгоритмом, предложенным для решения аналогичных задач С. Патанкаром. Это обусловлено тем, что в нашем случае нет необходимости в использовании итерационного процесса по согласованию полей скорости и давления. Последнее стало возможным благодаря отказу от требования консервативности на уровне элементарной расчетной ячейки. Однако на участке стабилизированного течения схема становится консервативной. Кроме этого, всегда имеется баланс массы по сечению канала или камеры ибо это условие существенным образом используется при определении градиента давления. Во многих случаях этого оказывается более чем достаточно и решение получается близким к аналитическим распределениям локальных гидродинамических величин либо к экспериментальным данным.
Глава. 11. Введение в теорию подобия потоков однофазных и многофазных сред
Представленный выше материал показывает, что процесс получения решение задачи о динамике физической среды весьма сложен. Поэтому при построении решения данных течений часто обращаются к популярной в экспериментальных исследованиях теории подобия и методу анализа размерностей.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!