Актуальность проблемы комплексного физико-математического и численного моделирования теплогидрогазодинамических процессов

В основе часто используемых вычислительных технологий расчета сложных течений лежит концепция комплексного численного моделирования трубопроводных систем с использованием базовых моделей механики сплошной среды, численных методов механики неоднородных систем, турбулентных потоков. Как известно, такие технологии успешно применяются при решении многочисленных многомерных и многопараметрических производственных задач повышения безопасности, эффективности и экологичности промышленных трубопроводных сетей в газовой, нефтяной, химической промышленности. Вполне понятно, что такие технологии достаточно сложны и опираются на численный эксперимент.

Он представляется в виде этапов: 1) математической постановки задачи, включающей разработку и выбор математической модели; 2) построения методики решения задачи в целом со структурным анализом математической модели; 3) разработки алгоритма решения отдельных задач; 4) модульного анализа алгоритмов; 5) разработки проекта программы с описанием структуры данных, информационных потоков; 6) разработки программы или модификации существующих; 7) проведения тестовых расчетов; 7) выполнения собственно решения задачи.

Существенное значение при численном моделировании имеет факт уменьшения затрат на разработку и модификацию программы.

Здесь представлен оригинальный численный алгоритм со следующей спецификой, которую вносит априорная информация о характере течения среды в особых областях, в частности, в рециркуляционных зонах смешения и у стенки канала. Существование в пристеночной зоне трубопровода высоких поперечных градиентов искомых величин заставляет работать с неравномерными сетками. Кроме того, мы учитываем положительные моменты, которые дают маршевые методы и способы одновременного нахождения поля скорости и градиента давления. Поэтому сформулируем методику, широко апробированную на расчете внутренних течений, дающую удовлетворительные результаты анализа прямоточных и закрученных инертных и химически реагирующих сред в трубах и каналах с постоянной и переменной по длине площадью поперечного сечения.

Таким образом, в алгоритме используем сетки со сгущением узлов в особых областях (стенка-ядро), итерационные методы, экономичные неявные конечно-разностные схемы, а также схемы расщепления по физическим процессам.

2. Схема численного интегрирования уравнений приближения “узкого канала”.

При решении осесимметричных задач о течении вязкой несжимаемой жидкости/слабосжимаемого газа в каналах постоянного и переменного поперечного сечения в отсутствие влияния объемных сил используется следующая система уравнений импульсов и энергии:

. (1)

Т а б л и ц а 1

Коэффициенты обобщенного уравнения (1).

	Ф	Г	S
	U	n	-(¶P/¶x)/r
	0	n	-(¶P/¶r)/r-W^2/r
	W	n	-VW/r-nW/r^2
	T	a

Здесь n=m/r - коэффициент кинематической вязкости, a =l¤(rс) – коэффициент температуропроводности.

Рассмотрим ключевые моменты в способе получения численного решения в этом случае. Уравнение (1) перепишем следующим образом:

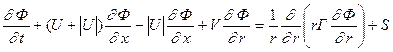. (2)

Представление конвективного члена в форме (2) позволяет реализовать двухстадийную схему получения решения, причем на первой стадии корректным образом осуществить маршевую процедуру расчета, связанную с последовательным продвижением в положительном направлении оси Ox. Это возможно, поскольку коэффициент (U+ | U |) при ¶Ф/¶x всегда неотрицателен даже при наличие в потоке интенсивных возвратных движений.

Рассмотрим аппроксимацию отдельных членов уравнения (2). Эволюционный член представим следующим образом:

. (3)

Здесь и ниже верхнее расположение двойных индексов будет отвечать верхнему слою по времени, нижнее – нижнему, индекс i соответствует выделенному сечению по длине канала, j отмечает положение при продвижении вдоль радиальной координаты r, t - шаг по времени.

По возможности будем ориентироваться на разработку неявных схем, поэтому ниже все пространственные производные будут расписаны с использованием сеточных значений функций на верхнем слое по времени. В связи с этим, аппроксимация (3) представляет собой одностороннюю разность по времени и имеет первый порядок точности относительно t. Все производные по радиальной координате будут аппроксимированы со вторым порядком точности относительно шага D r, а производные по продольной – с первым относительно шага D x. Сеточный шаблон, на котором расписаны пространственные производные, имеет следующий вид.

Рис.1. Сеточный шаблон, исполь-зуемый для записи разностного аналога уравнения (2).

Выпишем все необходимые аппроксимации:

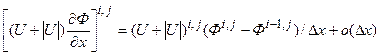, (4)

, (5)

, (6)

+

, (7)

где .

Далее введем обозначения:

Тогда разностный аналог, отвечающий уравнению (2) будет выглядеть следующим образом:

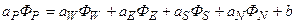, (8)

где

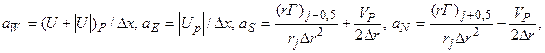
. (9)

Разностное уравнение (8) будем решать итерационным методом при обязательном прохождении двух последовательных этапов:

(I) , (10)

(II) . (11)

Здесь m – номер итерационного слоя. Рассмотрим подробнее первый этап вычислений. При однонаправленном во входном сечении движении жидкости значение субстанции Ф в этом сечении следует считать заданным. Мы уже упоминали, что при решении уравнений переноса на этапе (I) возможна реализация маршевой процедуры вычислений. Выполняя первый шаг этой процедуры найдем распределения Ф в первом сечении, далее во втором и т.д.

Таким образом, значения Ф_W, входящие в (10), всегда будут известны, а величину Ф_E на этом этапе берем с предыдущего итерационного слоя. Поэтому уравнения (10) можно переписать следующим образом:

, (12)

где .

Система уравнений (12) может быть эффективно разрешена методом прогонки. При Ф = W, T из (12) получаются разностные уравнения, не содержащие градиента давления и их решение не связано с какими–либо сложностями. Остановимся на особенностях разрешения системы U -уравнений, полученной на основе (12). В эту систему уже входят неизвестные величины (¶ P /¶ x)_p.

Для решения этой системы мы используем способ одновременного с полем скорости нахождения градиента давления. Следуя которому сеточные значения продольной компоненты вектора скорости записываются в виде, аналогичном [ 1 ], следующим образом:

(13)

где . Для простоты записи в (13) индекс i опущен. Отличие (13) от зависимости, предложенной в [1], состоит в том, что здесь сеточные значения П зависят не только от i, но и от j, то есть П является переменной по поперечному сечению величиной. Поэтому для определения продольного градиента давления недостаточно условия постоянства расхода и требуется некоторое уравнение, позволяющее его найти. В качестве такового используем уравнение количества движения в проекции на радиальное направление, разрешенное относительно поперечного градиента давления:

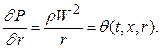(14)

Соотношение (14) выражает баланс поверхностных и массовых сил (в данном случае центробежных). Дифференцируя его по x и строя подходящий разностный аналог, будем иметь:

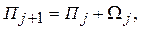(15)

где и Dr_j+1/2=r_j+1-r_j. Такое представление обеспечивает аппроксимацию с точностью до членов второго порядка малости относительно шага по радиальной координате.

При Ф=U из (12) имеем

, (16)

где

Подставляя в (16) зависимость (13), получим

(17)

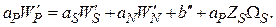(18)

Используя связь (13) и формулу трапеций при вычислении интегрального потока массы, можно получить соотношение:

. (19)

Здесь m_j =2prr_j Dr_j, узел N относится к оси течения, Q - расход жидкости через поперечное сечение канала.

Из (15) следует равенство

(20)

Тогда с использованием (19), (20) можем найти

(21)

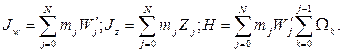где (22)

Зная величину продольного градиента давления на стенке П₀ и используя рекуррентное соотношение (15), можно рассчитать значения во всех точках поперечного сечения канала, которые необходимы для определения сеточных значений продольной компоненты скорости по (13). Величина поперечной компоненты скорости находится из уравнения неразрывности.

Дата добавления: 2014-11-29