Математическая формулировка процессов переноса в сплошной среде

Основная система уравнений гидромеханики имеет вид

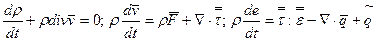. (1)

Система (1) справедлива для любых жидкостей и газов, но в данном виде не несет информации о свойствах СС.

Свойства среды должны задаваться выражениями для тензора напряжений (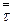) и вектора теплового потока (). Рассмотрим наиболее употребительные модели тензора напряжений и вектора теплового потока. В выражения для 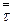и входят давление и температура, поэтому система (1) должна быть дополнена уравнением связи (ρ, T, p) ~ Ф(ρ, T, p)=0 – уравнением состояния.

Как было сказано выше, для ньютоновской среды имеем реологическое уравнение –– закон линейной связи между тензором напряжений и тензором скоростей деформаций - обобщенный закон Ньютона:

. (2)

Или в общей форме модель вязкой жидкости

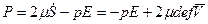. (3)

(3) – реологическое уравнение ньютоновской несжимаемой вязкой жидкости.

Определение. Вязкая среда несжимаема, если для нее div 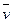=0, ρ=const, тогда - скорость звука равна бесконечности (∞).

1.1. Понятие о газообразных средах.

Определение. Вязкая теплопроводная сжимаемая СС - газ, если в ней возмущения распространяются с конечной скоростью распространения звука, , т.е. ρ=f(p,T).

Так, в изотермической среде

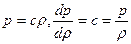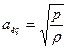, . (6)

В адиабатической среде – пренебрегая отводом тепла при распространении звука –

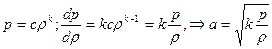. (7)

Когда газ – совершенный:

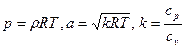. (8)

Замечание. Скорость распространения звука в совершенном газе зависит лишь от абсолютной температуры и от физических свойств газа.

Газ – агрегатное существование вещества. Реальный газ (РГ) - это газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия. Для описания свойств РГ применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева ().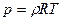

Общая запись модели РГ - , где - коэффициент сверхсжимаемости, функуция от .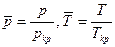

Уравнение Ван-дер-Ваальса состояния РГ

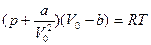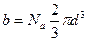, (9)

где 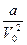- внутреннее давление, обусловленное силами притяжения молекул, b - поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами.

Уравнение состояния Бертло

. (10)

Здесь постоянные а, b связаны с параметрами критического состояния: p_k, V_0k, T_k.

Уравнение состояния Вукаловича-Новикова

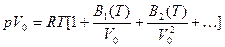, (11)

где B₁, B₂, … - вириальные коэффициенты сложного вида, вычисление которых проводится с учетом ассоциации молекул – объединения под влиянием Ван-дер-Ваальсовых сил притяжения.

1.2. Простейшие модели материальных сред. Существуют процессы, в которых необходимо учитывать малые изменения плотности жидкости. В этих условиях используют модель упругой жидкости

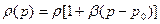, (1)

где - коэффициент сжимаемости: 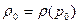, где p₀ – нормальное давление.

Если ввести модуль упругости K=1/β, то (1) имеет вид

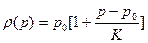
Модель с тепловым расширением жидкости(ТР) учитывает: при нагревании - среды расширяются, при охлаждении – сжимаются. Здесь ρ=ρ(T):

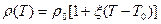, (2)

где 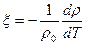- коэффициент объемного расширения; ρ_0, T₀ – плотность, температура в нормальных условиях.

Модель с барическим и тепловым расширением ρ=ρ(p,T):

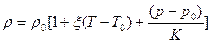. (3)

Модель неньютоновских жидкостей. Так, жидкости, моделируемые условием 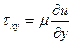- называются ньютоновскими вязкими жидкостями. Существуют среды, в которых связь τ=f(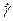) – нелинейная (здесь 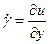). Это неньютоновские среды.

Пример. Модель степенной жидкости Оствальда

. (4)

Здесь связь между τ в слоях жидкости степенная

Кажущаяся вязкость в среде –

, (5)

где k, n – коэффициенты в среде.

Определение. Если n<1, то жидкости называются псевдопластичными (сюда относятся суспензии, вязкие жидкости с взвесью мелких частиц). При n>1 – среды – дилатантные (например, крахмальный клейстер).

Пример. Вязко-пластическая среда с предельным напряжением сдвига; модель “жидкости” Шведова-Бингама (сюда относятся высокопарафинистые и застывающие нефти, глинистые растворы, лаки, краски):

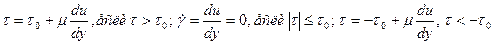. (6)

Физический смысл (6). Пока τ не превышает по mod некоторую предельную величину τ₀ (является предельным напряжением сдвига), течение такой среды не начинается (в этом случае 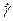=0). Среда течет как вязкая жидкость, если 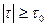, при этом .

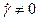Дата добавления: 2014-11-29