
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическая формулировка проблемы
|
|
|
|
Система дифференциальных уравнений, определяющая теплообмен при турбулентном течении однородного инертного потока слабосжимаемого газа в канале с изотермической стенкой включает уравнения: неразрывности, осредненные уравнения Навье – Стокса (динамические уравнения Рейнольдса), энергии, которые в тензорной форме были представлены выше и имеют вид:
 (2)
(2)
 (3)
(3) 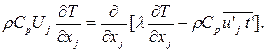 (4)
(4)
Переменность теплофизических свойств от температуры определяется зависимостью Саттерленда:
 (5)
(5)
где 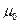 – динамический коэффициент вязкости при нормальных условиях
– динамический коэффициент вязкости при нормальных условиях  ; T – локальная температура; С – эмпирическая постоянная для закона (5), отвечающая конкретной газообразной среде. В случае анализа жидких капельных сред переменность теплофизических свойств учитывается формулой Рейнольдса-Филонова:
; T – локальная температура; С – эмпирическая постоянная для закона (5), отвечающая конкретной газообразной среде. В случае анализа жидких капельных сред переменность теплофизических свойств учитывается формулой Рейнольдса-Филонова:
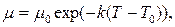 (6)
(6)
где k – опытная константа.
Заметим, что в случае анализа ламинарного режима течения и теплообмена система (5.2) – (5.4) вырождается в систему уравнений Навье – Стокса и энергии с напряжениями  ,
, 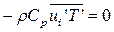 , для решения которых используются технологии, сообщенные выше. При турбулентных процессах систему (2) - (4) необходимо дополнить зависимостями, определяющими коэффициенты турбулентного обмена
, для решения которых используются технологии, сообщенные выше. При турбулентных процессах систему (2) - (4) необходимо дополнить зависимостями, определяющими коэффициенты турбулентного обмена 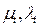 .
.
3. Модель турбулентности к замыканию уравнений, определяющих течение и теплоперенос во внутренних системах
Учитывая замечания к моделированию турбулентности, высказанные во введении, остановимся на моментной теории и многопараметрических (двухпараметрических тепловых и динамических) моделях. Тогда для напряжений Рейнольдса и турбулентных потоков тепла по подходу Колмогорова – Прандтля будем иметь:
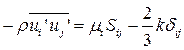 ; (7)
; (7)
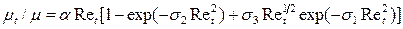 ; (8)
; (8)
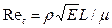 ; (9)
; (9)
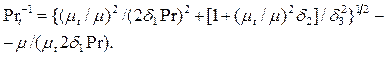 (10)
(10)
Замыкание определяющих уравнений проводится по K – L – модели, так как она более экономична при получении решения и эффективна в описании низкорейнольдсовых процессов. Ее транспортные уравнения имеют вид:
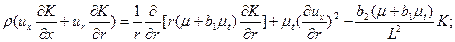 (11)
(11)
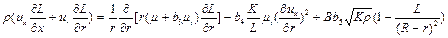 . (12)
. (12)
Значения констант в k-L модели следующие:
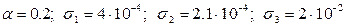 ;(5.14)
;(5.14)

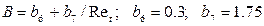 . (13)
. (13)
В определении турбулентных тепловых потоков  также используются двухпараметрические модели, представляющие уравнения для автокорреляций пульсаций температуры (энтальпии), скорости ее диссипации и имеют структуру, подобную уравнениям (11), (12):
также используются двухпараметрические модели, представляющие уравнения для автокорреляций пульсаций температуры (энтальпии), скорости ее диссипации и имеют структуру, подобную уравнениям (11), (12):
 |
(14)
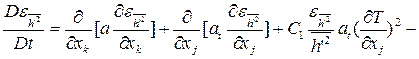
 (15)
(15)
 (16)
(16)
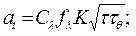 (17)
(17)
 (18)
(18)
 (19)
(19)
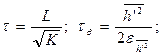 (20)
(20)
4 Краевые условия. Для осредненных и пульсационных гидродинамических характеристик необходимые краевые условия к интегрированию определяющих уравнений имеют вид (см. рис. 2):
1. На оси  условия симметрии
условия симметрии  ;
;
2. На входе  ,
,  , где
, где
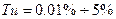 – интенсивность турбулентности, интегральный масштаб турбулентности
– интенсивность турбулентности, интегральный масштаб турбулентности 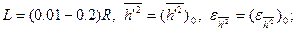
3. На стенке  выполняются условия прилипания, как для осредненных, так и пульсационных характеристик
выполняются условия прилипания, как для осредненных, так и пульсационных характеристик  ;
;  ;
; 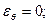
4. На выходе 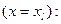


|
Глава 10. Современные методики математического моделирования и расчета турбулентных течений
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 495; Нарушение авторских прав?; Мы поможем в написании вашей работы!