Основные теоремы

1 теорема. У подобных явлений одноименные числа подобия одинаковы.

Эта теорема указывает условия, при которых результаты, полученные при исследовании математической модели, могут быть перенесены на натуральный объект.

Доказательство теоремы иллюстрируется конкретным примером подобия гидродинамических и тепловых процессов.

2 теорема. Подобны только те явления условия однозначности, которых подобны.

Теорема показывает как входные и начальные условия в математической модели подобных процессов определяют решения задач данного класса. Доказательство для газожидкостных систем.

3 теорема (π-теорема Ваши-Бекингема). Связь между (n+1) размерными параметрами (a₁, a₂, …, a_k, a_k+1, …,a_n) в безразмерном виде имеет соотношение между (n+1-k) величинами П₁, П₂, …, П_n-k. Здесь П₁, П₂, …, П_n-k - безразмерные комбинации из (n+1) величин.

Теорема указывает путь получения чисел подобия, при этом использование безразмерной формы записи исходных уравнений и ГУ позволяет снизить степень конкретизации данной задачи, т.е. результаты единичного расчета в безразмерном виде оказываются справедливыми по отношению к бесконечному набору геометрически и физически подобных процессов. Дается доказательство теоремы для широкого круга термодинамических процессов.

В качестве законов подобия для тепловых и динамических процессов стоит упомянуть такие как законы Стокса, Блазиуса, Никурадзе – для гидродинамических течений, Кейса-Кроуссольда, Диттуса-Белтера – для тепловых, Шервуда-Джиллилаида – для диффузионных. Они касаются формулировки интегральных параметров тепло- и массообмена внешних и внутренних процессов. Что качается локальных параметров, то здесь стоит вести речь о законах для конкретных типов течений и тепломассопереноса, например, вязкого, вязко-инерционного, вязко- инерционно- гравитационного, прямоточного и закрученного потока, инертного и химически реагирующего, изотермического и неизотермического течения однофазного и многофазного течения смеси. Все рассматриваются в курсе.

Глава 12. Уравнение Бернулли в механике жидкости. Основные теоремы

Математический аппарат данной главе ориентируется на теории и методику расчета течений идеальной и вязкой среды, опираясь на допущение о упрощении процесса течения. Остановимся на этих сведениях.

1. Вводные замечания, определения и теоремы

Напомним, что выше мы приняли. Считаем невязкой жидкостью жидкость, в которой не может возникнуть никакого сrоль угодно малого касательного напряжения. Линией тока (ЛТ) наз. линия, проведенная в жидкости таким образом, что касательная к ней в каждой точке совпадает с направлением скорости жидкости в этой точке. ЛТ показывают, как каждая частица движется в данный момент времени. Траектории – как данная частица движется в каждый момент. ЛТ, проведенная через каждую точку замкнутой кривой образует трубку тока. Струйкой тока, или элементарной трубкой тока наз. трубка тока, поперечное сечение которой является кривой бесконечно малого размера.

Теорема. В установившемся движении жидкости произведение скорости на площадь поперечного сечения постоянно вдоль жидкой струйки тока.

Следствие 1. Нить тока расширяется в местах, где скорость жидкости уменьшается, и сужается в местах, где скорость жидкости увеличивается.

Следствие 2. Струйка тока не может оканчиваться внутри жидкости, если скорость не равна бесконечности в соответствующей точке.

Теорема Бернулли (специальная форма). В установившемся движении жидкости величина

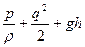имеет постоянное значение в каждой точке одной и той же линии тока. Здесь p,ρ,q – соответственно давление, плотность, скорость; g – ускорение силы тяжести, h – высота рассматриваемой точки над фиксированной горизонтальной плоскостью.

Замечания к теореме Бернулли.

Специальная форма теоремы Бернулли получена в предположении:

1) что действует только одна внешняя сила - сила тяжести. Поле силы тяжести консервативно – это значит, что работа, совершенная силой тяжести при движении тела от точки P к другой точке Q, не зависит от пути, а зависит только от высоты точки Q по отношению к точке P. Консервативное поле сил приводит к понятию потенциальной энергии, которая измеряется работой, совершенной телом при переходе от одного определенного положения к другому. Чтобы потенциальная энергия единицы массы в точке могла иметь определенный смысл, необходимо, чтобы работа сил поля не зависела от пути, по которому совершается переход в эту точку. Если в общем случае Ω – потенциальная энергия единицы массы в консервативном поле сил, то теорема Бернулли в общей форме будет: 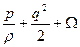имеет постоянное значение вдоль линии тока.

2) жидкость несжимаема и имеет постоянную плотность. В общем случае баротропного потока (p=p(ρ)) теорема принимает форму: выражение имеет постоянное значение вдоль линии тока.

Постоянная в теореме Бернулли. Для отдельной линии тока по теореме Бернулли (ТБ) 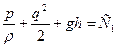. Для другой - 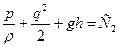, где С₁, C₂ – постоянные вдоль линий тока. Когда движение безвихревое, то константа одинакова для всех линий тока.

Гидродинамическое давление (ГД). При установившемся движении ТБ позволяет выяснить характер давления. В покоящейся жидкости имеется в каждой точке гидростатическое давление p_H и по закону Архимеда имеем, что на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной им жидкости. Частицы жидкости также подчиняются этому закону, и поэтому они находятся в равновесии под действием гидростатического давления p_H и силы тяжести. Поэтому величина p_H/ρ+gh является константой для всей жидкости. Если жидкость движется, то подъемная сила также может действовать. Тогда p=p₀+p_H и по ТБ имеем 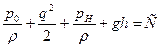. Следовательно,

- новая константа. (1)

Т. обр., (1) выражает ТБ для отсутствия силы тяжести. Здесь р₀ – гидродинамическое давление или давление, обусловленное движением. Из (1) следует, что гидродинамическое давление больше там, где скорость меньше, а также что наибольшее ГД имеет место в точках с нулевой скоростью.

Поток в канале. Рассматривается задача об установившемся течении в канале с горизонтальным дном (h- высота поверхности над дном) и прямоугольным поперечным сечением ширины b. При давлении на свободной поверхности р=1атм из теоремы Бернулли следует q² +2gh=const (*). Если ширина канала слабо меняется, то мало меняется и скорость. Тогда дифференцируя (*) имеем udu+gdh=0. С учетом уравнения неразрывности ubh=const, которое может быть записано, как 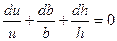, исключая du имеем .

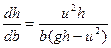Таким образом, глубина и ширина канала увеличиваются одновременно тогда и только тогда, когда [ 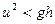] скорость u меньше скорости распространения длинных волн в канале.

1.1. Интеграл Бернулли и усложненная термодинамика.

В термодинамике энтальпия единицы массы газа определяется как

(2)

Следовательно, при малых изменениях . Согласно 1 началу термодинамики , если dq=0 (процесс адиабатический), то di=dp/ρ. Тогда интеграл Бернулли, с учетом связи , будет

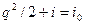(3)

Здесь i₀ – значение энтальпии при q=0.

Если в (3) включить (2), то имеем . Здесь E- внутренняя энергия, состоящая для многоатомных газов из энергий поступательного, вращательного и колебательного процессов.

Сообщается об особенностях записи интеграла Бернулли для двухатомных газов, неравновесных процессов.

1.2. Интеграл Лагранжа.

Сделаем предположения:

1) жидкость идеальная; 2) баротропная; 3) массовые силы консервативны; 4) движение безвихревое. Тогда, для безвихревого движения идеальной жидкости уравнение движения будет иметь вид в форме Громека

. (4)

Т.к. жидкость баротропна, то

(5)

По допущения 3) имеем 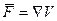. Из 4) следует, что 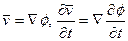. С учетом этих положений получим

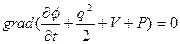. (6)

Из (6) следует, что

. (7)

(7) – интеграл Лагранжа.

1.3. Интеграл Эйлера-Бернулли. Предположим, что выполняются предположения для вывода интеграла Лагранжа и движение установившееся. Тогда имеет место (7). Поскольку v_x, v_y, v_z и φ не зависят от времени, то f(t) переходит в постоянную:

. (8)

Здесь постоянная С одна и та же для всего потока в отличие от интеграла Бернулли, в котором С на разных линиях тока различна.

Дата добавления: 2014-11-29