
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статическое давление жидкости на твердые поверхности. Закон Архимеда
|
|
|
|
Рассмотрим в жидкости какую-либо поверхность АВ площадью S (рис. 8).
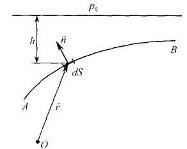 Рис. 8
Рис. 8
| Равнодействующая R сил давления, действующих на эту поверхность, и их момент равны
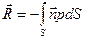 , (26) , (26)
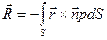 , (27)
где ň- внешняя нормаль, направленная внутрь жидкости, ř - радиус-вектор точки на АВ. , (27)
где ň- внешняя нормаль, направленная внутрь жидкости, ř - радиус-вектор точки на АВ.
|
В случае несжимаемой жидкости, находящейся в ноле сил тяжести, давление в точках поверхности АВ в соответствии с формулой (13) равно
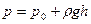 , (28)
, (28)
где ри - давление на свободной поверхности. С учетом формулы (14) равенство (28) может быть представлено как
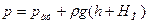 . (29)
. (29)
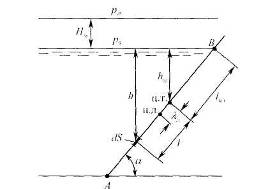 Рис. 9.
Рис. 9.
| Пусть поверхность АВ представляет собой плоскость, наклоненную к горизонту под углом α(рис. 9). Все векторы ňпараллельны друг другу и из равенств (26), (28) и (29) имеем
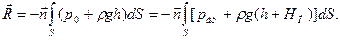 (30)
Так как (30)
Так как 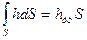 , где hцт -расстояние от свободной поверхности до центра тяжести плоскости АВ, то из формулы (30) следует, что , где hцт -расстояние от свободной поверхности до центра тяжести плоскости АВ, то из формулы (30) следует, что
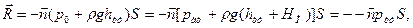
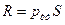 . (31) . (31)
|
где рцт =р0 +ρghцт =рат + pg{hцт +HП) - давление в центре тяжести АВ.
Если сила Řрассчитывается не по абсолютному давлению, а по избыточному, то очевидно, что
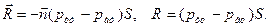 (32)
(32)
Определим положение центра давления, то есть точки приложения равнодействующей Ř. Момент Mх этой силы относительно оси Ох, проходящей через центр тяжести плоскости АВ (рис. 9), равен
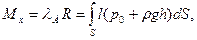 (33)
(33)
где λД - расстояние от центра тяжести АВ до центра давления, l - расстояние от центра тяжести до элемента dS.
Из рис. 9 видно, что h=(lцт +l)sinα. Подставив это выражение в формулу (33), получим
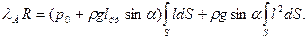 (34)
(34)
Имея в виду, что статический момент площади S относительно оси, проходящей через ее центр тяжести, равен нулю, то есть, что
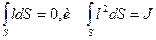 ,
,
где J - момент инерции площади S относительно той же оси, из формулы (34) получим, с учетом равенства (31),
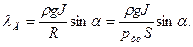
Если расчет силы R ведется по избыточному давлению, то в соответствии с (32)
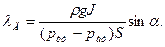
Если pцт >pат, то λД >0 и центр давления лежит ниже центра тяжести.
Рассмотрим случай криволинейной поверхности АВ. Проектируя равенство (26) на вертикальную ось 0z и какую-либо из горизонтальных осей, например, Ох, получим
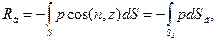 (35)
(35)
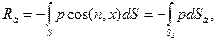 (36)
(36)
где dSг, dSв,-проекции dS соответственно на горизонтальную плоскость, перпендикулярную Oz, и вертикальную плоскость, перпендикулярную Ох.
Подставив в равенства (35) и (36) значение p из (29), имеем
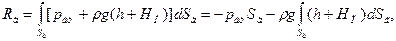 (37)
(37)
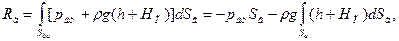 (38)
(38)
Интеграл
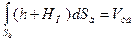
представляет собой объем тела давления Vтд, образованный поверхностью АВ, ее проекцией на пьезометрическую плоскость и вертикальными образующими. Формулу (37) можно представим, в виде
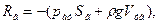 (39)
(39)
Интеграл
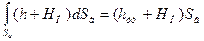
представляет собой статический момент вертикальной проекции Sв.относительно пьезометрической плоскости. Поэтому из (38) имеем
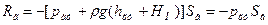 . (40)
. (40)
где рцт - давление в центре тяжести площади Sв.
Для сил, рассчитанных по избыточному давлению, вместо формул (39) и (40) имеем
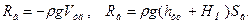
Заметим, что формула (31) совпадает с формулой (40), если в ней заменить S на.S'B.
|
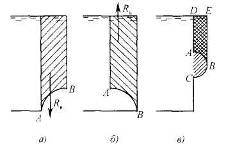
Примеры построения тел давления приведены па рис. 10. На рис. 10a объем тела давления, построенный па поверхности АВ, находится в жидкости. На рис. 10б объем тела давления лежит вне жидкости. Такое тело давления называется фиктивным и ему присваивается знак «-». На рис. 10в представлен случай, когда вертикальные образующие пересекают поверхность А ВС более чем в одной точке. Поэтому тела давления строятся отдельно для участков АВ (тело ABDE) и ВС (тело CBED).
Рис. 10.
Вертикальная составляющая сил давления на ABC определяется как разность вертикальных составляющих сил, действующих на АВ и ВС.
Если поверхность S замкнутая и целиком погруженная в жидкость, то в соответствии с формулой (26) и теоремой Гаусса-Остроградского
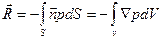 , (41)
, (41)
где V - объем жидкости, ограниченный поверхностью S. В ноле силы тяжести в соответствии с уравнением Эйлера (2) 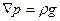 и из (41) получим
и из (41) получим
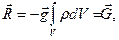 (42)
(42)
где Ğ - вес жидкости в объеме V. Формула (42) выражает закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила R, равная весу жидкости в объеме погруженного тела. Сила R называется также гидростатической подъемной силой.
Из формулы (27) и георемы Гаусса-Осгроградского имеем
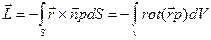 . (43)
. (43)
Радиус-вектор 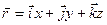 и, следовательно,
и, следовательно,

Подставив это соотношение в формулу (43) и учитывая, что 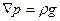 , а
, а 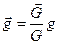 .
.
Получим
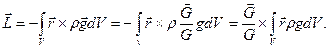 (44)
(44)
Радиус-вектор центра тяжести объема К равен
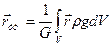
и формулу (44) с учетом равенства (42) можно представить в виде
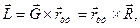
откуда следует, что линия действия гидростатической подъемной силы Ř
проходит через центр тяжести объема V.
Глава 8. Динамика вязкой жидкости и газа. Уравнения законов сохранения массы, импульса и энергии
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 805; Нарушение авторских прав?; Мы поможем в написании вашей работы!