
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Потенциальные вихревые движения идеальной среды. Основные теоремы
|
|
|
|
Общая постановка задач о течении идеальной нетеплопроводной жидкости.
Система определяющих уравнений включает.
1. Уравнение неразрывности-  .
.
2. Уравнение движения сплошной среды, которые в проекциях на оси координат имеют вид:
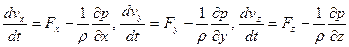 . (10)
. (10)
(10) – уравнения Эйлера – уравнения движения идеальной жидкости.
3. Уравнение энергии. Т.к. жидкость нетеплопроводна, то  . Имеем
. Имеем
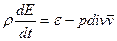 .
.
3. Уравнение состояния – f(p,ρ,T)=0 и выражение для внутренней энергии E через какие-либо 2 величины из 3 (p,ρ,T).
Более подробно система имеет вид:
 ;
;
 ;
;
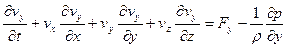 ; (11)
; (11)
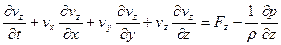 ;
;
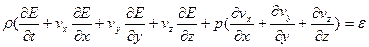 ;
;
f(p,ρ,T)=0.
Здесь E=E(p,T).
Зам.: Этой системе удовлетворяют все течения идеальной нетеплопроводной жидкости, как установившиеся, так и неустановившиеся, а также относящиеся к обтеканию жидкостью различных тел при разнообразных условиях.
Рассмотрим безвихревые движения, т.е. движения, для которых
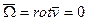 (12)
(12)
или в проекциях на ост координат
 . (13)
. (13)
При выполнении (12) линейная дифференциальная форма 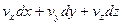 будет полным дифференциалом некоторой функции φ для любого фиксированного момента времени. Иначе говоря, существует такая функция φ(x,y,z,t), для которой полный дифференциал при достаточном постоянном t вычисляется по формуле
будет полным дифференциалом некоторой функции φ для любого фиксированного момента времени. Иначе говоря, существует такая функция φ(x,y,z,t), для которой полный дифференциал при достаточном постоянном t вычисляется по формуле  . Но поскольку
. Но поскольку
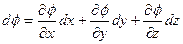 , то имеем
, то имеем  . (14)
. (14)
Т.е. компоненты скорости есть частные производные от функции φ(x,y,z,t) по координатам. Функцию φ наз. потенциалом скоростей, а безвихревые движения наз. потенциальными. Для установившихся движений φ =φ(x,y,z). Тогда (14) равносильны равенству  , которое следует из (12).
, которое следует из (12).
Вихревые движения идеальной жидкости. Это движения, у которых вектор вихря во всех точках области или какой-либо ее части не равен нулю: Ω≠0. При изучении вихревых движений приходится иметь дело с такими понятиями, как циркуляция скорости и поток вектора вихря скорости через поверхность. Ниже рассматриваются основные теоремы вихревого движения идеальной жидкости (Стокса, Томсона, Лагранжа, Гельмгольца).
Теорема Стокса. Поток вектора вихря через поверхность S равен циркуляции скорости по контуру, ограничивающему эту поверхность:  .
.
Теорема Томсона. Если жидкость идеальна, баротропна и массовые силы имеют потенциал, то циркуляция скорости по любому замкнутому контуру не зависит от времени.
Теорема Лагранжа. Пусть выполнены условия теоремы Томсона, т.е.жидкость идеальна, баротропна и массовые силы консервативны. Тогда, если в некоторый момент времени t0 в фиксированной массе жидкости нет вихрей, то их не было в предыдущие и не будет в последующие моменты времени.
Теоремы Гельмгольца.
1 теорема. Если жидкие частицы в какой-либо момент времени t0 образуют вихревую линию, то эти же частицы образуют вихревую линию во все последующие и все предыдущие моменты времени.
2 теорема. Интенсивность вихревой трубки постоянна по ее длине и не изменяется со временем.
Совокупность вихревых линий, проведенных через замкнутый контур, образует вихревую трубку. Интенсивностью вихревой трубки называют циркуляцию скорости по контуру, охватывающему трубку 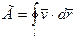 . Такое понятие имеет смысл, если интенсивность (т.е. циркуляция Г) не зависит от положения контура l по длине трубки. По теореме Стокса
. Такое понятие имеет смысл, если интенсивность (т.е. циркуляция Г) не зависит от положения контура l по длине трубки. По теореме Стокса 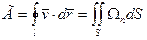 , S – поверхность, пересекающая вихревую трубку.
, S – поверхность, пересекающая вихревую трубку. 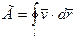
Глава 7. Статика жидкостей и их свойства. Основные законы равновесия
1. Уравнения равновесия жидкости и газа
Как отмечалось выше, в гидростатике рассматриваются законы равновесия жидкости (газа), находящейся в покое. Если жидкость (газ) находится в состоянии покоя относительно стенок сосуда, в котором она заключена, а сосуд покоится или движется с постоянной скоростью относительно земли, то покой называется абсолютным. Если жидкость покоится относительно стенок сосуда, а сосуд движется относительно земли с ускорением, то покой называется относительным. Движение жидкости в случае относительного покоя можно рассматривать как переносное. Из приведенных определений вытекает, что в случае абсолютного покоя на жидкость действует сила тяжести, а в случае относительного покоя - сила тяжести и сила инерции переносного движения.
Так как в покоящейся жидкости скорости деформации εik=0, то из реологического уравнения для вязкой жидкости (см.выше реологический закон) имеем
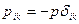 , (1)
, (1)
то есть в покоящейся жидкости действуют только нормальные сжимающие напряжения.
Зам.: По Л. Прандтлю «жидкостью называется такое тело, в котором в состоянии равновесия всякое сопротивление деформации равно нулю». Из этого определения следует, что 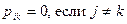 и, соответственно, εik=0.
и, соответственно, εik=0.
Величина этих напряжений не зависит от направления и равна давлению. Это давление называется гидростатическим.
Подставив соотношения (1) в уравнения движения сплошной среды в напряжениях, получим (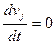 ):
):
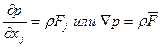 . (2)
. (2)
Уравнения (2) называются уравнениями Эйлера в гидростатике.
Умножив скалярно векторное уравнение (2) на единичный вектор  , имеем
, имеем
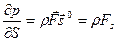 , (3)
, (3)
то есть изменение давления в каком-либо направлении 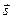 определяется проекцией напряжения массовой силы Fs на это направление.
определяется проекцией напряжения массовой силы Fs на это направление.
Умножим скалярные уравнения (2) на dxj. Так как при равновесии p=p(xi), то
 . (4)
. (4)
Поверхности, вдоль которых р = соnst, называются изобарами. Из равенств (4) следует, что уравнение изобары имеет вид
 , (5)
, (5)
где вектор dr лежит в плоскости, касательной к изобаре. Тогда из (5) вытекает, что напряжение массовой силы направлено по нормали к изобаре. Этот же вывод следует непосредственно из равенств (2).
Очевидно, что уравнения (2)-(5) в равной мере справедливы как для сжимаемых, так и для несжимаемых жидкостей.
Из уравнений (4) имеем, что
 , (6)
, (6)
где М0, М -точки, в которых гидростатическое давление равно соответственно р0 и р. Если напряжение массовой силы обладает потенциалом, то есть 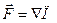 , то соотношение (6) принимает вид:
, то соотношение (6) принимает вид:
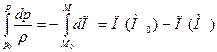 . (7)
. (7)
2. Равновесие жидкости в поле силы тяжести
 Рис. 6.1.
Рис. 6.1.
| При рассмотрении равновесия жидкости в поле силы тяжести введем систему координат Oxyz, где ось O z направлена против ускорения силы тяжести ĝ ( см. рис.1). В этом случае П= -g z, Fx, = Fy = 0, Fz =-g и уравнение (4) принимает вид:
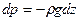 . (8)
В случае однородной несжимаемой жидкости р-const, из уравнения (6.8) имеем . (8)
В случае однородной несжимаемой жидкости р-const, из уравнения (6.8) имеем
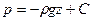 . (9) . (9)
|
Уравнение (9) справедливо для любой точки в объеме жидкости. Уравнение изобары имеет в рассматриваемом случае вид
 . (10)
. (10)
Таким образом, при равновесии жидкости, находящейся в поле силы тяжести, изобара представляет собой горизонтальную плоскость.
Для определения константы С в уравнении (9) необходимо задать граничные условия. Пусть при z=z0 p=p0 (см. рис. 1). Тогда
p-p0=ρg(z0-z), (11)
или
 . (12)
. (12)
Обозначив z0 -z=h, уравнение (11) можно представить в виде
p=p0+ρgh. (13)
где pgh - давление, создаваемое столбом жидкости высотой h.
Уравнение (8), или (12), обычно называются основными уравнениями гидростатики.
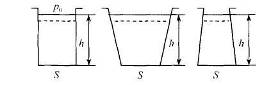 Рис. 2.
Рис. 2.
| Из (13) следует, что сила давления жидкости на дно сосуда с площадью основания S не зависит от его формы (рис. 2) и равна (p0 +ρgh)S. Данный результат обычно называется парадоксом Паскаля. [Бпез Паскаль (1623-1662). французский физик и математик]. Превышение абсолютного давления рабс над атмосферным pат, то есть разность pи=pабс-pа называется избыточным давлением. Величина pв =pа-pабс называется вакуумом. | |
 Рис.3.
Рис.3.
| Рассмотрим некоторые примеры на применение уравнений гидростатики. 1. Сообщающиеся сосуды (рис. 3). Давление на свободных поверхностях с координатами z1 Z/ и z, одинаково. Следовательно, они представляют собой участки одной изобарической поверхности и в соответствии с соотношением (6.9) z; = z-.. Этот же вывод следует из уравнения изобары (10). 2. Равновесие разнородных жидкостей. Пусть две несмешивающиеся жидкости с плотностями р1 и p2 находятся в состоянии равновесия. Давление при переходе через поверхность раздела меняется непрерывным образом. На поверхности раздела из уравнения (8) имеем dp=-ρ1gdz, dp =-ρ2 -gdz или p1,g dz = p2,g dz. Следовательно, dz =0 и граница раздела представляет собой горизонтальную плоскость z =const. | |
 Рис. 4.
Рис. 4.
| 3. Двухжидкостной манометр (рис. 4). Для определения разности давлений в системе, заполненной жидкостью плотности ρ1, используется манометр с рабочей жидкостью плотностью ρ2. В точках 4 и 5, лежащих на горизонтальной плоскости в одной и той же жидкости, p4=p5. В соответствии с уравнением (13)
 откуда следует, что р1 - р2 =gh{ρ2-ρ1).
откуда следует, что р1 - р2 =gh{ρ2-ρ1).
| |
 Рис. 5.
Рис. 5.
| 4. Пьезометрическая высота (рис. 5). Давление в несжимаемой жидкости можно измерять высотой столба этой же жидкости НП с помощью трубки А. Такая трубка называется пьезометрической.
Для точек 1 и 2 имеем:
 Тогда
Тогда 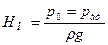 . (14)
Давление в любой точке сосуда равно . (14)
Давление в любой точке сосуда равно
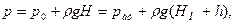
|
Высота Н называется пьезометрической, а поверхность, проходящая через уровень в пьезометре - пьезометрической плоскостью. Если p0> рат, то пьезометрическая плоскость
лежит выше свободной поверхности в сосуде, если p0< рат, то ниже.
5. Равновесие тяжелого газа. Для газа, находящегося в равновесии в поле силы тяжести, из (7) имеем
 (15)
(15)
Для вычисления интеграла в (15) необходимо задать зависимость р =p(ρ).
Ограничимся рассмотрением изотермического равновесия идеального газа при температуре Тb. Тогда ρ=p/(RT0) и из (15) получим:

Разлагая это выражение в ряд, имеем:
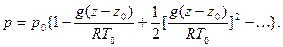
Если

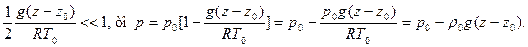 (16)
(16)
где ρ 0 - плотность газа при давлении p0 и температуре То. Из формулы (16) следует, что если z - z0 мало, то распределение давления в газе будет практически таким же, как в несжимаемой жидкости. Для воздуха газовая постоянная R=287дж/(кг град). Пусть T0=293°К. Тогда при z-z0<85м погрешность, даваемая формулой (16), будет меньше 1%.
3. Относительный покой жидкости
Как уже указывалось, при рассмотрении относительного покоя жидкости под напряжением массовой силы в уравнениях (2) следует понимать равнодействующую напряжений силы тяжести и силы инерции переносного движения.
Рассмотрим задачу о вращении с постоянной угловой скоростью ωсосуда с жидкостью вокруг вертикальной оси Оz (рис. 6). На элемент жидкости массой ∆ m действует сила тяжести и центробежная сила, напряжения которых равны
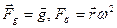 ,
,
где ř ~ вектор, направленный по кратчайшему расстоянию от оси вращения к рассматриваемому элементу. Проекции этих напряжений на выбранные оси координат O.xyz равны

Подставив эти значения в уравнения (4) и (5), имеем

Интегрируя эти соотношения, получим
 (17)
(17)
 (18)
(18)
 Рис.6.
Рис.6.
| Уравнение (17) дает закон распределения давления в жидкости, а соотношение (18) представляет собой уравнение семейства изобар, представляющих собой параболоиды вращения.
Для определения константы С в уравнении (17) и уравнении свободной поверхности (18) рассмотрим точку А пересечения свободной поверхности с осью 0z. Точка А имеет координаты (0, 0, z0), а давление в этой точке равно р0. Тогда из уравнений (17) и (18) имеем С = р0 +gz0, С1=gz0 и

|
Для определения высоты Н параболоида положим в уравнении (20) r = R, где R - радиус сосуда.
Тогда

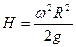 .
.
Из уравнения (20) имеем
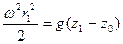 ,
,
 где z1 - координата точек пересечения вертикальных прямых r1=const со свободной поверхностью. Подставив это соотношение в уравнение (19), получим
где z1 - координата точек пересечения вертикальных прямых r1=const со свободной поверхностью. Подставив это соотношение в уравнение (19), получим
 (21)
(21)
Таким образом, если отсчитывать координату z от свободной поверхности, то распределение давления по вертикали во вращающемся сосуде будет таким же, как и в покоящейся жидкости. Это объясняется тем, что проекция силы инерции на ось 0z равна нулю.
Полученный результат следует также непосредственно из формулы (3). Действительно, в рассматриваемом случае
 ,
,
откуда после интегрирования сразу получается формула (21).
Рассмотрим теперь движение сосуда с жидкостью по наклонной плоскости с постоянным ускорением ā(рис. 7).
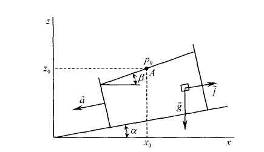 Рис. 7.
Рис. 7.
| Проекции напряжения массовых сил на координатные оси равны
 где а - угол наклона плоскости к горизонту,
где а - угол наклона плоскости к горизонту,  . Подставив эти значения в уравнения (4) и (5), имеем . Подставив эти значения в уравнения (4) и (5), имеем

|
Из соотношения (23), представляющего собой уравнение семейства изобар, получим
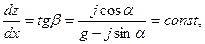 (24)
(24)
то есть изобары представляют собой плоскости, наклоненные иод углом β к горизонту.
Интегрируя уравнение (22), получим закон распределения давления
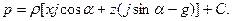
Для определения константы интегрирования С положим, что в точке H(xo,0,z0) р=р0. Тогда
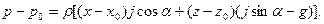 (25)
(25)
Рассмотрим некоторые частные случаи.
а) Спуск по вертикальной стене, то есть а =π/2. Из формулы (24) следует, что β=0, z=const. Изобары представляют собой горизонтальные плоскости. Из формулы (25) имеем

При свободном падении j = g и р = р0, то есть давление во всех точках жидкости одинаково. Единственной действующей на жидкость силой будет поверхностное натяжение, под действием которого жидкость стягивается в шар.
б) Скольжение по плоскости без трения. В этом случае j=gsinαи из формулы (24) получим, что tgβ=tgα, то есть эквипотенциали параллельны плоскости скольжения. Из формулы (25) имеем

|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1084; Нарушение авторских прав?; Мы поможем в написании вашей работы!