Приклад розв’язання типових задач

Задача 1. За даними про територію, чисельність населення і валовий внутрішній продукт двох країн обчислити відносні величини: інтенсивності,

порівняння.

Країна	Територія, тис. км.^2	Чисельність населення, тис. осіб.	ВВП, млрд. грош. од.
А		16 390	32 483
В	1 285	18 710	16 866

Розв’язок:

Вихідна інформація дає змогу встановити відносні величини інтенсивності: густота населення; ВВП на душу населення.

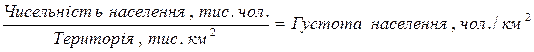
Країна А 16 416: 912 = 18,0 (чол./км²)

Країна в 17 990: 1 285 = 14,0 (чол./км²)

Висновок: таким чином, за результатами проведених розрахунків в країні А густота населення складає 18 осіб на 1 км² території, в країні В – 14 осіб на 1 км² .

Країна А 32 483: 16 416 = 1978,74 (грош. од.)

Країна В 16 866: 17 990 = 937,52 (грош. од.)

Висновок: таким чином, за результатами проведених розрахунків в країні А ВВП на душу населення складає 1978,74 грош. од., в країні В – 937,52 грош. од.

Для того щоб визначити відносні величини порівняння зіставимо дані двох країн, взявши за базу порівняння країну А.

Для обчислення відносних порівняння, будуємо робочу таблицю:

Показники	Країна	Відносні показники порівняння (дані країни Б до даних країни А), %
А	В
Територія, тис. км.^2	912,0	1 285,0	140,9
Чисельність населення, тис. чол.	16 416,0	17990,0	114,2
ВВП, млрд. грош. од.	32 483,0	16 866,0	51,9
Густота населення, чол/км ^2	18,0	14,0	77,8
ВВП на душу населення, грош. од.	1978,7	937,5	47,4

Висновок: Так, в країні В порівняно з країною А густота населення менша на 22,2 % (77,8% - 100%), а виробництво ВВП на душу населення – на 52,6 % (47,4% -100%).

Задача 2. Визначити структуру роздрібного товарообороту за рік якщо є такі дані:

Товарні групи	Товарообіг, тис. грн.
попереднього року	звітного року
Продовольчі	5 100	5 250
Непродовольчі	4 525	5 044
Разом	9 625	10 294

Розв’язок:

Визначаємо відносну величину структури за формулою:

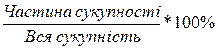
Для обчислення відносної величини структури будуємо робочу таблицю:

Структура роздрібного товарообороту:

Товарні групи	Попереднього року	Звітного року
Продовольчі	(5 100/9 25)*100=53,0%	(5 250/10 294)*100=51,0%
Непродовольчі	(4 525/9 25)*100=47,0%	(5 044/10 294)*100=49,0%
Разом	100,0%	100,0%

Висновок: У складі роздрібного товарообороту в звітному році порівняно з попереднім зменшилася питома вага продовольчих товарів на 2,0% (51,0-53,0) та водночас зросла питома вага непродовольчих товарів також на 2,0% (49,0-47,0).

Задача 3. Статутний фонд акціонерної компанії сформований 6 засновниками; розмір внеску кожного з них становить, млн. грош.од.: 6; 10; 12; 9; 7; 4. Визначте середній внесок одного засновника.

Розв’язок:

У наведеному прикладі варіюючи ознака – внесок одного засновника.. Числові значення ознаки називаються варіантами.

Середній внесок одного засновника визначаємо за формулою середньої арифметичної простої оскільки вихідні дані не згруповані.

Задача 4. За даними розподілу робітників цеху за кількістю виготовлених деталей визначити середній денний виробіток деталей:

Денний виробіток деталей, штук	Кількість робітників, осіб

Розв’язок:

Вихідна інформація наведена у вигляді дискретного варіаційного ряду розподілу, де денний виробіток деталей це варіанта, а кількість робітників – частоти. Для визначення середнього денного виробітку скористаємося логічною формулою визначення середнього виробітку відповідно до економічного змісту цього показника:

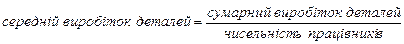
Звідси середньо денний виробіток продукції визначаємо за формулою середньої арифметичної зваженої оскільки вихідні дані згруповані.

Задача 5. Відомі дані про розподіл устаткування на підприємстві за строком експлуатації:

Строк експлуатації, років	Кількість устаткування
до 5
5-10
10-15
15-20
20-25
25-30
більше 30
Разом

Визначити середній строк експлуатації устаткування на підприємстві.

Розв’язок:

Логічна формула для визначення середнього строку експлуатації устаткування буде мати вигляд:

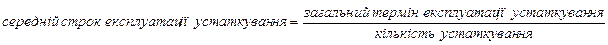
За умовою задачі строк експлуатації устаткування в кожній групі наведений у вигляді інтервалу, тобто кожна група ряду розподілу має мінімальне і максимальне значення (закриті інтервали), перша група має мільки максимальне значення і остання група має тільки мінімальне значення. (відкриті інтервали).

Середній строк експлуатації слід обчислювати за формулою середньої арифметичної зваженої, але попередньо треба визначити центр інтервалу.

Центр інтервалу =

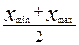
Для відкритих інтервалів умовно величина інтервалу першої групи дорівнює величині інтервалу наступної групи, а величина інтервалу останньої групи – величині інтервалу попередньої групи.

Отже:

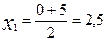
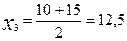
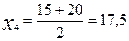
Для визначення середнього строку експлуатації устаткування побудуємо робочу таблицю:

Розрахунок середнього стажу роботи

Строк експлуатації, років	Кількість устаткування,	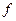Цент інтервалу
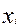
до 5		2,5
5-10		7,5
10-15		12,5
15-20		17,5
20-25		22,5
25-30		27,5
більше 30		32,5
Разом		х

Подальший розрахунок здійснюємо за формулою середньої арифметичної зваженої:

Висновок: середній строк експлуатації устаткування на підприємстві 14,5 років.

Дата добавления: 2014-11-29