Приклади розв’язання типових задач

Задача 1. Наведені дані про обсяг виготовленої продукції робітниками за зміну:

Порядковий номер робітника	Обсяг виготовленої продукції за зміну, шт.
Бригада № 1	Бригада № 2
Разом

Необхідно за допомогою показників варіації дати оцінку продуктивності праці робітників двох бригад.

Розв’язок:

Перш за все визначимо середній випуск продукції робітниками цеху № 1 та № 2. Обчислення середнього рівня здійснюємо за формулою середньої арифметичної простої:

;

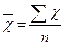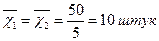
Середній рівень продуктивності праці в обох бригадах однаковий, проте відхилення виробітку окремих членів бригади від середнього показника – різне.

Для характеристики розмірів коливань ознаки по відношенню до середньої величини обчислимо показники варіації. Для здійснення обчислень побудуємо робочу таблицю:

Порядковий номер робітника	Обсяг виготовленої продукції за зміну, шт	Відхилення
Бригада 1	Бригада 2
Бригада 1	Бригада 2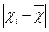
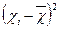
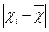
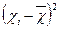
Разом

Варіаційний розмах обчислюємо за формулою:

R = x _max – x _min

для першої бригади R =18-2= 16 шт.

для другої бригади R =12-8= 4 шт.

Середнє лінійне відхилення обчислюємо за формулою:

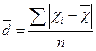
Воно складатиме:

для першої бригади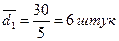

для другої бригади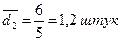

Таким чином, індивідуальні значення виробітку продукції окремих робітників мають такі відхилення від середнього виробітку: у першій бригаді 6 штук, у другій – 1,2 штук. Отже, за показником виробітку продукції за зміну, друга бригада однорідніша за першу.

Середній квадрат відхилень (дисперсію) обчислюємо за формулою:

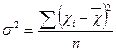
для першої бригади

для другої бригади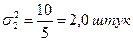

Середнє квадратичне відхилення обчислюємо за формулою:

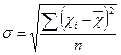
для першої бригади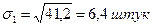

для другої бригади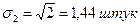

Середнє квадратичне відхилення є «мірилом» надійності середньої. Чим менше середнє квадратичне відхилення, тим об'єктивніше середня арифметична відображує всю сукупність.

Як видно з розрахованих показників, у другій бригаді дисперсія і середнє квадратичне відхилення набагато менші, ніж у першій, що свідчить про високу надійність середньої у другій бригаді.

Обчислюємо відносні показники варіації у наведеному прикладі:

Коефіцієнти варіації	1 бригада	2 бригада
квадратичний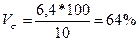

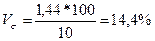
Квадратичний коефіцієнт варіації у першій бригаді дорівнює 64%, що свідчить про досить значні коливання індивідуальних значень змінного виробітку робітників відносно середнього виробітку в цілому по бригаді, тобто сукупність робітників першої бригади за рівнем продуктивності праці якісно неоднорідна, і відповідно, типовість середньої величини виробітку у цій бригаді невелика. У другій бригаді цей показник становить 14,4%, що свідчить про середні коливання середнього виробітку і сукупність робітників цієї бригади за рівнем продуктивності праці досить однорідна.

Задача 2. В таблиці наведені дані про стаж роботи робітників підприємства:

Стаж роботи, роки	Кількість робітників, осіб
до 5
5-10
10-15
15-20
20 і більше
Разом

Розрахувати показники варіації, на підставі отриманих показників зробити висновки.

Розв’язок:

Вихідні дані є згрупованими. Оскільки відомі значення варіанти (стаж роботи) і частоти (чисельність робітників), то для обчислення середнього стажу роботи використовуємо формулу середньої арифметичної зваженої.

Для обчислення середньої арифметичної в інтервальному ряді розподілу спочатку визначаємо центри заданих інтервалів стажу роботи.

Оскільки у невідома нижня межа першого інтервалу і верхня межа п’ятого інтервалу, то ми їх умовно вважаємо за розміром сусіднього інтервалу. За розрахунковими даними обчислюємо середній стаж.

Середній стаж роботи робітників підприємства становить 9,5років.

Для здійснення обчислень показників варіації побудуємо робочу таблицю:

Стаж роботи	Кількість робітників, f	Розрахункові показники
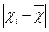
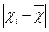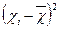
хі	хіf		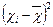f		f
До 5		2,5
5-10		7,5
10-15		12,5
15-20		17,5
20 і більше		22,5
Разом		-		-		-

Для визначення міри коливань стажу роботи окремих робітників відносно середнього стажу роботи в цілому по підприємству обчислюємо за формулами показники варіації:

Варіаційний розмах:

R = χ_max - χ_min = 22,5 – 2,5 = 20 років

Середнє лінійне відхилення:

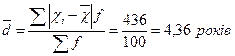
Середній квадрат відхилень (дисперсію):

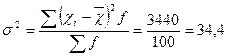
Середнє квадратичне відхилення:

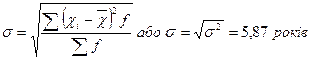
Квадратичний коефіцієнт варіації:

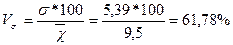
Висновок: таким чином, середній стаж роботи робітників даного підприємства становить 9,5 років. Стаж роботи окремих робітників відрізняється від середнього показника на 4,36 років за середнім лінійним відхиленням і на 5,39 років за середнім квадратичним відхиленням. Коефіцієнт варіації 56,7% свідчить про значні коливання стажу роботи окремих робітників по відношенню до середнього стажу роботи на підприємстві, а це означає, що сукупність робітників підприємства за стажем роботи не можна вважати якісно однорідною. Відповідно, обчислений показник середнього стажу роботи не буде типовим для робітників цього підприємства, оскільки індивідуальні значення стажу роботи мають значні коливання і суттєво відрізняються від середнього стажу роботи.

Задача 3. На основі даних про розподіл магазинів за розміром товарообігу визначити моду та медіану:

Групи магазинів за розміром товарообігу, тис. грн.	Кількість магазинів
200-300 300-400 400-500 500-600 600-700 700 і більше

Розв’язок:

Відповідно до визначення модою є варіанта, яка має найбільшу частоту. У нашому прикладі мода знаходиться в інтервалі від 400-500, оскільки цей інтервал має найбільшу частоту.

Для визначення моди використовуємо формулу:

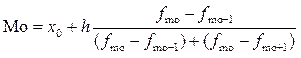
де 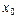та h – відповідно нижня межа та ширина модального інтервалу, 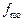, , 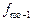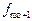– частоти (частки) відповідно модального, передмодального та післямодального інтервалів.

За даними таблиці модальним є інтервал 400-500, що має найбільшу частоту 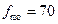; ширина модального інтервалу h = 100 (500-400); нижня межа х ₀ = 400; передмодальна частота 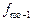= 30, післямодальна – 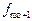= 60. За такого співвідношення частот модальне значення:

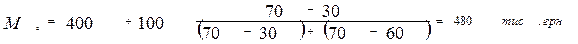Для визначення медіани в інтервальному ряду розподілу обчислимо кумулятивні частоти:

Групи магазинів за розміром товарообігу, тис. грн.	Кількість магазинів	Накопичувальні частоти
200-300 300-400 400-500 500-600 600-700 700 та більше		40 (30+10) 110 (40+70) 170 (110+60) 195 (170+25) 200 (195+5)

Визначаємо інтервал, у якому знаходиться медіана. Оскільки медіана – це значення ознаки, що знаходиться в середині упорядкованого ряду розподілу й відповідно, ділить ряд на дві рівні частини.

Для встановлення медіанного інтервалу необхідно визначити накопичену частоту кожного наступного інтервалу доти, поки вона не перевищить половини суми накопичених частот. У нашому випадку 100 тис. грн. (200/2). медіанним є інтервал із границями 400-500 тис. грн.

Знаходимо медіану за формулою:

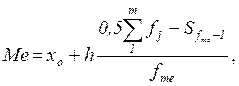
де x ₀ та h — відповідно нижня межа та ширина медіанного інтервалу; f _me — частота медіанного інтервалу; 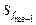— кумулятивна частота передмедіанного інтервалу.

За даними таблиці половина обсягу сукупності 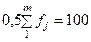припадає на інтервал 400 — 500 з частотою 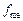= 70; передмедіанна кумулятивна частота 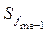= 40.

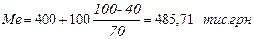
Отже, медіанне значення: 485, 71 тис. грн..

Висновок: найбільша кількість магазинів має товарообіг 480 тис. грн., половина магазинів має товарообіг до 485,71 тис. грн., а друга половина – понад 485,71 тис. грн.

Дата добавления: 2014-11-29