Алгоритм решения задачи. Алгоритм решения задачи – точное предписание последовательности действий

Алгоритм решения задачи – точное предписание последовательности действий. Ряд задач, связанных с оптимизацией логистических систем, целесообразно решать методом динамического программирования. Под динамическим программированием понимается вычислительный метод, опирающийся на аппарат рекуррентных (возвратных) уравнений, разработанных Р. Беллманом. Этот метод применяется при решении задач упорядочения перебора вариантов. Метод динамического программирования применяется в том случае, если задачу можно представить как многошаговую. На каждом шаге выявляют вариант, при котором выбранная последовательность вариантов наилучшая по критерию эффективности. Пошаговое представление процесса позволяет свести решение многомерных задач к решению одномерных многошаговых. Для поставленной задачи алгоритм сводится к следующему.

1. Исходные значения времени выполнения логистических функций t_ij и стоимостных затрат C_ij записываются в виде матриц (3) и (4).

2. Производится преобразование матриц, обеспечивающие следующее соотношение величин t_ij и C_ij по столбцам:

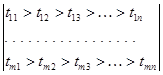
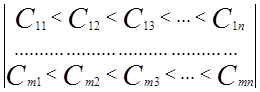
3. При больших значениях n и m (количестве альтернативных вариантов выполнения логистических функций и количестве элементов логистической системы), задача формирования оптимальной логистической системы решается как многомерная.

Использование динамического программирования, а именно функциональных уравнений Р. Беллмана, позволяет свести решение многомерных задач к решению многошаговых одномерных.

Для шага 1 [первый столбец матриц (3) и (4)], имеем:

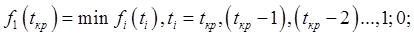, (5)

где f₁(t_кр) – зависимость стоимостных затрат при выполнении первой логистической функции от времени ее выполнения, т.е. первый столбец исходной матрицы C_ij (4). Задаваясь значениями t_ij от t_кр до 0, осуществим выбор наиболее эффективного способа выполнения первой логистической функции, допустив что вся логистическая система состоит только из нее.

Для шага 2 (с учетом обоих столбцов матрицы):

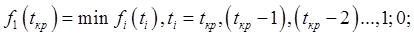(6)

При выборе оптимального варианта для m – функции, (шага - m)

(7)

Примечание. Для удобства проведения расчетов без применения вычислительной техники, исходные данные в приведенных ниже задачах позволяют в алгоритме задаваться значениями

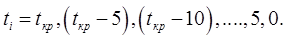
Примечание. Для удобства проведения расчетов без применения вычислительной техники, исходные данные в приведенных ниже задачах позволяют в алгоритме задаваться значениями

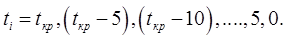
Исходные данные по вариантам

Исходные данные временных затрат на выполнение логистических функций по вариантам (в раб. дн)

Таблица 7.7.

№ ва-риан-та	Максималь-но допустимое время tкр	Логистические функции
Доставка материала, складирова-ние	Изготовле-ние, сборка	Складирова-ние готовой продукции	Транспорти-ровка	Распределе-ние товара на оптовой базе

Исходные данные стоимостных затрат при выполнении логистических функций по вариантам (тыс. руб.)

Таблица 7.2.

№ варианта	Логистические функции
Доставка материала, складирование	Изготовление, сборка	Складирование готовой продукции	Транспортировка	Распределение товара на оптовой базе
С 1 по 25

Исходные данные с учетом поставленной задачи можно представить в виде матриц: Исходные данные с учетом поставленной задачи можно представить в виде матриц:

для вариантов курсовой работы с 1 по 11:	для вариантов курсовой работы с 12 по 25:

для вариантов курсовой работы с 1 по 25:

С

Преобразуем матрицы, вычтя из каждого столбца его минимальное значение. На эту же величину уменьшим и значение t_кр.

Получим:

для вариантов курсовой работы с 1 по 11:	для вариантов курсовой работы с 12 по 25:
t	t

C

.

Далее производим решение в соответствии с приведенным выше алгоритмом.

Примечание. Индивидуальность вариантов определяется различием критического времени (t_кр), соответствующего выпуску определённой программы.

Дата добавления: 2014-11-29