ЗАКОН ГЕССА 2 страница

Враховуючи перший закон термодинаміки та основні за­кони термохімії, знаючи хімічний склад продуктів харчування та енергетичні характеристики поживних речовин, технолог повинен уміти з урахуванням фаху людини складати оптималь­ний раціон харчування (енергоменю). Значно складніше обрати необхідне для організму співідношення, наприклад, тваринних і рослинних жирів. Відповідні рекомендації розробляють біологи, лікарі, дієтологи.

4. ДРУГЕ НАЧАЛО ТЕРМОДИНАМІКИ

Як зазначалось, І закон термодинаміки характеризує енергетичні баланси і дає змогу обчислити теплові ефекти хімічних реакцій за стандартних умов (закон Гесса), але він не відповідає на питання щодо можливості перебігу того або іншого процесу.

Друге начало термодинаміки ґрунтується на закономірностях, згідно з якими можна знаходити напрям процесу і визначати умови, за яких можливі ті чи інші процеси. Другий закон термодинаміки, так само як і перший, є постулатом, він був сформульований на основі досвіду. Сфера застосування цього закону обмежена: лише для макросистем, які складаються з великої кількості частинок.

Другий закон термодинаміки має важливе значення для хімії. Він встановлює можливість, напрям і межу перебігу самодовільних процесів, тобто вказує, який процес і в якому напрямку може протікати при певних умовах (температура, тиск, концентрація), не поглинаючи енергію зовні.

Історично другий закон термодинаміки було сформульовано раніше першого. Треба відзначити, що з часом він отримував нові визначення, які ставали все більш точнішими. Вперше основне положення другого закону термодинаміки було висловлено М.В.Ломоносовим у 1747р.

Перше математичне формулювання умов перетворення теплоти в корисну роботу було зроблено Саді Карно (1824р.), у працях німецького фізика Клаузіуса (1850р.) і англійського фізика Томсона (лорда Кельвіна) у 1854р. Були розвинені ідеї, які вийшли далеко за межі першопочаткової теплотехнічної задачі. Пізніше Максвелл, Больцман і Гіббс встановили зв’язок другого закону термодинаміки з молекулярно-кінетичними уявленнями. Це привело до статистичного тлумачення другого закону термодинаміки.

Термодинамічні величини поділяють на інтенсивні та екстенсивні.

Інтенсивні величини не залежать від кількості речовини або маси системи і при взаємодії системи вони прямують до вирівнювання – Т, Р, концентрація.

Екстенсивні величини пропорційні до кількості речовини і при взаємодії системи вони складаються (додаються) – об’єм, маса, теплоємність.

Є багато різних формувань ІІ закону термодинаміки, всі вони логічно пов’язані між собою.

Одне з формулювань ІІ закону термодинаміки.

Самодовільно можуть відбуватися лише такі процеси, у результаті яких вирівнюються ті або інші фактори інтенсивності. Рівновазі відповідають однакові значення фактора інтенсивності в кожній частині системи.

Для самодовільного перебігу процесу мають бути створені умови, які сприяють такому вирівнюванню. Наприклад, для теплообміну потрібні різні температури в різних частинах системи або в системі та навколишньому середовищі.

У реальних процесах переважно вирівнюється не один, а кілька факторів інтенсивності.

М.В.Ломоносов, а пізніше Р. Клаузіус (1850р.) сформулювали ІІ закон термодинаміки так: теплота не може самодовільно переходити від холодного тіла до гарячого.

Іншими словами, процеси можуть самодовільно відбуватись лише в напрямі, який веде до вирівнювання факторів інтенсивності - теплота може переходити від гарячого тіла до холодного; газ може розширюватися лише з одночасним зниженням тиску; електричний струм протікає від вищого потенціалу до нижчого тощо.

Кожний процес, що протікає самодовільно, приводить систему до рівноваги. Рівновага досягається і в хімічних реакціях. Розрізняють оборотні і необоротні хімічні реакції. Слід вказати, що теоретично всі реакції є оборотними, а необоротність пов’язана зі зміщенням рівноваги.

В залежності від умов, при яких проходить дана реакція (концентрація с, тиск Р, температура Т), може змінюватися напрямок реакції і стан рівноваги. Наприклад,

2Н₂ + О₂ 2Н₂О

ця реакція при низьких температурах самодовільно йде в прямому напрямку і рівновага настає при досить малих концентраціях водню і кисню. При високих температурах самодовільно йде зворотна реакція – розкладання води на водень і кисень. Рівновага встановлюється при досить великих концентраціях цих газів в системі. Як видно на прикладі даної реакції, зміна умов (температури) обумовлює і направлення процесу, і стан рівноваги.

Зазвичай для реалізації хімічного процесу в промисловості необхідно заздалегідь знати умови, при яких він буде йти в необхідному направленні і з найбільшим виходом продуктів реакції. Визначити ці умови можна тільки, використовуючи основні положення другого закону термодинаміки.

5. ТЕРМОДИНАМІЧНІ ПОТЕНЦІАЛИ І ФАКТОРИ

Самовільні процеси відбуваються з розсіюванням теплової енергії. Для кількісної характеристики процесу розсіювання енергії у 1865р. німецьким фізиком Р.Клаузіусом була введена термодинамічна функція – ентропія S.

Ентропією називають функцію, за допомогою якої можна визначити напрям та умови рівноваги процесу.

Ентропія ізольованої системи збільшується і в стані рівноваги набуває максимального значення. Отже, її можна використовувати як критерій напряму перебігу таких процесів.

Ентропія є мірою розсіяної (знеціненої) енергії, ентропія системи – це міра невпорядкованості її стану.

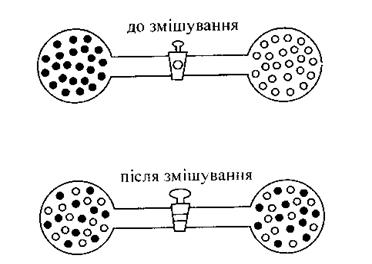
Рис. 3. Самовільне змішування двох газів

Для розуміння цього поняття уявимо, що два гази, які містять однакову кількість молекул, знаходяться в двох частинах посудини, яка розділена перетинкою-краном (рис.3). Якщо відкрити кран, то розпочнеться дифузія газів, яка приведе до їх змішування. Цей процес відбувається довільно і закінчиться рівномірним розподілом молекул по всьому об'єму. Інші варіанти розподілу менш ймовірні. Тобто, в системах із великого числа частинок, довільно можуть протікати процеси переходу від менш ймовірного до більш ймовірного стану.

Чим більша ентропія, тим менша частка енергії може перетворитися в роботу, тобто ентропія виступає як міра необоротності процесу.

Самовільно відбуваються такі процеси, в яких ентропія зростає (для ізольованих систем):

S > 0

Це твердження витікає із математичного виразу ентропії, який одержав Клаузіус для ізотермічного процесу:

S ≥ Q / Т

Знак нерівності відноситься до необоротних процесів, а знак рівності - до оборотних. (Оборотним є процес, який складається з послідовних рівноважних станів). Якщо процес не оборотний, а самовільний (спонтанний), то частина теплоти втрачається, наприклад, через теплопровідність, тертя тощо.

Ентропія є також мірою термодинамічної ймовірності стану системи.

Кожному стану термодинамічної системи однозначно відповідає певне значення ентропії S, яке тим більше, чим більша ймовірність даного стану (макростану) системи W.

Ймовірність даного стану системи, що складається з великої кількості мікрочастинок, визначається кількістю способів та варіантів їх розподілу (кількістю мікростанів).

Австрійський фізик Л.Больцман встановив функціональний зв'язок між ентропією S і ймовірністю стану системи W:

S = k• 1n W

де k = R/ N_а - стала Больцмана (відношення газової сталої R до сталої Авогадро Na).

Отже, чим більшою кількістю мікрочастинок представлена дана система, тим більше варіантів розподілу цих частинок, при яких може бути реалізований даний макростан, тим вище значення ентропії і тим більш знеціненим буде наявний у системі запас енергії. Таким чином ентропія характеризує ту частину енергії, яка не перетворюється в роботу.

До росту ентропії приводить підвищення температури речовини, оскільки зростає інтенсивність руху частинок і, відповідно, число способів їх розміщення. Ентропія зростає при фазових переходах, при випаровуванні, при хімічних реакціях, особливо, якщо в результаті збільшується число молекул.

Процеси, для яких ΔS > 0:

1. Розширення газів

2. Фазовий перехід від твердого до рідкого та газоподібного.

3. Розчинення кристалів.

Процеси, для яких ΔS < 0:

1. Стиснення і зрідження газів

2. Конденсація.

3. Кристалізація.

Наряду із зменшенням ентальпії (ΔН < 0) направленість будь-якого фізичного або хімічного процесу визначається і збільшенням ентропії (ΔS > 0). Для того, щоб порівняти ці величини, необхідно виразити їх в однакових одиницях:

[ΔН ] = Дж/моль, а [ΔS ] = Дж/моль•К

Тому необхідно домножити ΔS на Т.

Тоді можна говорити про ентальпійний (ΔН) та ентропійний (ТΔS) фактор процесу. Добуток ΔS на Т є правомірним, бо підвищення температури збільшує хаотичний рух частинок, тобто збільшує безлад.

При відсутності ентропійного фактора (ΔS = 0) самодовільно можуть йти процеси, що супроводжуються позитивним тепловим фактором (ΔН < 0).

Якщо система ізольована і її ентальпія постійна (ΔН = 0), тобто відсутній ентальпійний фактор, то самодовільно будуть йти процеси, що супроводжуються збільшенням ентропії (ΔS > 0). При цій умові збільшується об’єм системи.

В тому випадку, коли в системі діють два фактори, напрямок процесу визначається їх сумарним впливом, причому зменшення ентальпії (ΔН) характеризує прагнення системи до порядку, збільшення ентропії (ΔS) – до безладу.

Якщо система знаходиться в стані рівноваги, то справедливе рівняння:

ΔН = ТΔS або ΔН - ТΔS = 0

Для процесів, що йдуть самовільно, при умові одночасної дії ентропійного (ΔS > 0) і ентальпійного (ΔН < 0) факторів справедливе співвідношення:

ΔН - ТΔS < 0, або (Н₂ - Н₁) – Т (S₂ - S₁) < 0

Н₂ - Н₁ - ТS₂ + ТS₁ < 0

(Н₂ - ТS₂) - (Н₁ - ТS₁) < 0

Функцію (Н – ТS) називають ізобарно-ізотермічним потенціалом (скорочено ізобарним потенціалом) або енергією Гіббса і позначають

буквою G.

G = H - TS ΔG = ΔH - TΔS

Якщо Р = const, то ΔG < 0

Отже, в системах, що знаходяться при постійних Т і Р, самовільно можуть протікати процеси, що супроводжуються зменшенням ізобарно-ізотермічного потенціалу.

Для процесів, що йдуть при постійному об’ємі (V = const) ΔН = ΔU, одержимо:

ΔН = ΔU = ТΔS або ΔU - ТΔS = 0

Функцію (U – ТS) називають ізохорно-ізотермічним потенціалом (скорочено ізохорним потенціалом) або енергією Гельмгольца і позначають буквою F:

F = U - TS або Δ F = ΔU - TΔS

Якщо V = const, то ΔF < 0

Отже, в системах, що знаходяться при постійних Т і V, самодовільно можуть протікати тільки процеси, що супроводжуються зменшенням ізохорно-ізотермічного потенціалу.

Зроблені висновки про самодовільне протікання процесів тільки при ΔG < 0 та ΔF < 0 можна вважати формулюваннями другого начала стосовно і до процесів хімічних. Якщо ΔG < 0, то протікання реакції принципово можливе, але практично може не здійснюватись внаслідок кінетичних труднощів. Чим більш негативне значення ΔG, тим більш реакційно здатною буде система. Зміна енергії Гіббса відображає вплив на спрямованість протікання процесу як ентальпійного фактору ΔН, так і ентропійного TΔS.

У залежності від температури, вплив одного з цих факторів на значення і знак ΔG і, звісно, на напрямок процесу може бути визначальним (табл. 1.2).

Якщо значення ΔG > 0 і ΔF > 0, то можна стверджувати, що процес принципово неможливий, його самодовільне протікання суперечить основному закону термодинаміки.

Відомо, що будь-який зворотній хімічний процес протікає самодовільно в направленні, що наближує систему до рівноваги. При рівновазі ΔG або ΔF = 0, а потенціали G або F мають мінімальні для даних умов значення.

Таблиця 1.2.

Типи реакцій та умови їх протікання в залежності від ΔН, ΔS, ΔG

Тип реакції	Знак	Принципова можливість і умови протікання реакції
ΔН	ΔS	ΔG
	-	+	-	Можлива при будь-якій температурі
	+	-	+	Принципово неможлива
	-	-	- +	Можлива при низьких температурах
	+	+	+ -	Можлива при високих температурах

Таким чином, використовуючи ізобарно-ізотермічний потенціал (енергію Гіббса), можна отримати відповідь на питання принципової можливості самодовільного протікання того чи іншого процесу в певному напрямку. Це дає можливість керувати складними технологічними процесами і досягати запланованих результатів (табл.1.2).

6. РОЗРАХУНОК ТЕРМОДИНАМІЧНИХ ПОТЕНЦІАЛІВ В ХІМІЧНИХ РЕАКЦІЯХ

В виробничих або лабораторних умовах частіше зустрічаються процеси, що йдуть при постійних Р і Т, тому для встановлення можливості протікання процесу необхідно визначити значення ΔG.

Для розрахунку ΔG в хімічних реакціях користуються рівнянням:

ΔG = Σ (ΔG_утвор._.) _кінц - Σ (ΔG_утвор.) _вих.

Де ΔG_утвор – зміна ізобарного потенціалу при утворенні з’єднань з простих речовин.

Значення ΔG_утвор. сильно залежить від температури, тому розрахунки ведуть для стандартних умов, що дозволяє одержати значення ΔG, які можна порівняти.

Стандартними умовами вважається тиск Р = 101,3 кПа і температура 25^оС (298 К).

Величину ΔG_утвор. при стандартних умовах прийнято позначати як: ΔG^о₂₉₈, для більшості речовин вона відома і приведена в довідниках.

Приклад розрахунку:

Розрахувати ΔG^о₂₉₈, для реакції:

СО_{2 (г)} + 2Н₂О_(р.) = СН_{4 (г)} + 2 О_{2 (г)}

і на основі одержаних даних визначити принципову можливість реакції.

З довідника візьмемо стандартні потенціали утворення речовин, що приймають участь в реакції:

СО_{2 (г)} ΔG^о₂₉₈ = - 394,64 кДж/моль,

Н₂О_(р.) ΔG^о₂₉₈ = - 237,4 кДж/моль

СН_{4 (г)} ΔG^о₂₉₈ = - 50,85 кДж/моль

О_{2 (г)} ΔG^о₂₉₈ = 0

Розв’язок:

ΔG = Σ (ΔG_звор.) _{кінц __} - Σ (ΔG_{звор.) вих.}

ΔG^о₂₉₈ = (ΔG^о_СН4 + 2∙ΔG^о₀₂) - (ΔG^о_СО2 + 2 ΔG^о_Н2О)

ΔG^о₂₉₈ = (-50,85 +0) – (-394,64 +2∙(-237,4)) = - 50,85 – (-394,64 – 474,8) = - 50,85 + 394,64 + 474,8 = - 50,85 + 869,44 = 818,59 (кДж/моль).

Одержана зміна ізобарного потенціалу ΔG^о₂₉₈ має досить велике позитивне значення. Тому можна стверджувати, що ця реакція при стандартних умовах неможлива, можлива зворотна реакція. Але зробити такий висновок для інших умов неможливо. Зміна ізобарного потенціалу речовин, які приймають участь в реакції, залежить від температури (ΔG=ΔН – ТΔS), причому ця залежність для різних речовин неоднакова. Це може привести до того, що при Т = 298 К ΔG > 0, тобто реакція принципово неможлива, а при іншій температурі ΔG < 0 і тоді можна говорити про можливість даної реакції.

!ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ

Задача 1.

Розрахувати зміну стандартної ентропії утворення (^∆S⁰ утв) етанолу з елементів, користуючись табличними даними абсолютних ентропій речовин при 25⁰С (стандартних ентропій речовин S⁰ ₂₉₈).

2С + 3Н₂ + 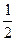О₂ С₂Н₅ОН

Табличні дані абсолютних ентропій речовин Речовина:	S^0 298,
C(т) графіт	5,21
О2 (г) S^0	205,18
Н2 (г)	130,52
С2Н5ОН (р)	160,78

Розв’язання:

S⁰ ₂₉₈ = ∑ S⁰ ₂₉₈ пр - ∑S⁰ ₂₉₈ вих.

Підставивши величини S⁰₂₉₈ в рівняння для даної реакції, одержимо з врахуванням коефіцієнтів рівняння реакції:

^∆S⁰утв.= 160,78 – (2 · 5,21 + 3 ·130,52 + 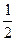· 205,18) = - 343,79

Задача 2.

Розрахуйте зміну ентропії при плавленні 10г води. Питома теплота плавлення q = 19,12

Розв’язання.

Зміна ентропії для ізотермічного зворотного процесу можна розрахувати по формулі.

^∆S⁰ = ,

де ∆S - зміна ентропії процесу;

Q - теплота процесу;

Т - температура, К.

Температура плавлення льоду 273,16 К. Таким чином, _∆Sпл. 1г води знайдемо як

∆S = = = 0,07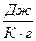

Для плавлення 10г речовини будемо мати 0,07 ·10 = 0,7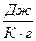

Задача 3.

Знайти ентальпію процесу, що відповідає найпростішому рівнянню фотосинтезу, по величинам ентальпій утворення вихідних речовин та продуктів реакції:

6СО₂ + 6Н₂О С₆Н₁₂О₆ + 6О₂ + ∆ Нх.

Розв’язання.

Стандартні ентальпії утворення речовин, що беруть участь в цьому процесі знайдемо у таблиці:

_∆ Н⁰₂₉₈ (С₆Н₁₂О₆) = - 2820,1

_∆ Н⁰₂₉₈ (СО₂) = 393,5

_∆ Н⁰₂₉₈ (Н₂О) = 241,8

_∆ Н⁰₂₉₈ (О₂) = О (як проста речовина).

Скористаємося для розв’язання задачі законом Гесса. Для цього запишемо термохімічні рівняння всіх процесів утворення вказаних речовин.

6С + 30₂ + 6Н₂ = С₆Н₁₂О₆ + ∆Н₁ (1)

С + О₂ СО₂ + ∆Н₂ (2)

Н₂ + 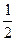О₂ = Н₂О + ∆Н₃ (3)

Помножимо рівняння (2) і (3) на (-6) і додаємо всі ці рівняння.

В результаті одержимо:

6С +30₂ + 6Н₂ –6С - 6О₂ - 6Н₂ – 3О₂

С₆Н₁₂О₆ + ∆Н₁ - 6СО₂ - 6∆Н₂ - 6Н₂О - 6∆Н₃

Проведемо алгебраїчне додавання:

- 6О₂ + С₆Н₁₂О₆ + ∆Н₁-6∆Н₃ = -6∆Н₃ -6СО₂ –6Н₂О

перенесемо перенесемо

вправо вліво

Маємо кінцевий запис:

6СО₂ + 6Н₂О = С₆Н₁₂О6 + 6О₂ +

В результаті одержимо рівняння фотосинтезу, яке ми шукали, з якого видно, що: ∆Н_х = ∆Н₁ - 6∆Н₂ - 6∆Н₃

Тоді: ∆Н_х =-2820,1 – 6 ∙ (- 393,5) – 6 ∙ (241,8) = 991,7 ()

САМОСТІЙНА РОБОТА

@Задача 4.

Знайдіть ентальпію реакції за величинами ентальпій утворення вихідних речовин та кінцевих продуктів (у відповідності з варіантом)

№ варіанту	Процес
	2С2 Н2 + 5О2 = 4СО2 +2Н2О
	СН4 +2О2 = СО2 + 2Н2О
	2СН3ОН + 3О2 = 4Н2О + 2СО2
	СН3СООН +2О2 = 2СО2 + 2Н2О
	СαО + Н2О = Сα (ОН)2
	2СО + 4Н2 = С2Н5ОН + Н2О
	АІ2О3 + 3SO3 = AI2 (SO4)3
	4NH3 + 5O2 = 4 NO + 6H2O
	Fе2О3 + 2АI= 2 Fе + АІ2О3
	Fе2О3 +3СО = 2Fе + 3СО2

@Задача 5.

Знайдіть зміну ентропії у вказаних нижче процесах при стандартних умовах.

№ варіанту	Процес
	N2 + 3H2 = 2 NH3
	H2 + I2 = 2HI
	2NO + O2 = 2NO2
	H2 +CI2 = 2HCI
	Кипіння 1 кмоля води ∆h кип (пит) = 2,257

@Задача 6.

Обчисліть стандартні значення теплового ефекту ∆Н₂₉₈⁰, зміну ентропії ∆ S₂₉₈⁰ та ізабарно–ізотермічний потенціал ∆G₂₉₈⁰ реакції (за вказаним варіантом). Зробіть висновок про можливість протікання реакції в стандартних умовах.

Реакції:

Варіант 1

Mq SO_4(к) + Sі0_{2 (КВ)}+Н₂О_(Р) = Mq SіO_3(к) +Н₂SO_4(Р)

Варіант №2.

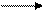Mq SO_3(ТВ) MqO_(ТВ) + SО_2(г)

Варіант №3.

СО_2(г) + SO₂ (г) СО_(г) + SO₃ (г)

Варіант №4.

S О_2(г) + NO_{2 (г)} SO₃ (г) + NO(г)

Варіант №5.

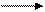ТіО₂ (тв) + MqO_(ТВ) MqТіО_3(ТВ)

Варіант №6.

SіО_{2 (тв) +} MqO_(тв) MqSіО_{3 (тв)}

Варіант №7.

MqSO_{4 (тв)} + СО MqO_(тв) + SO₂ + СО₂

@Задача 7.

Обчисліть стандартні значення теплового ефекту ∆ Н ₂₉₈⁰, зміну ентропії ∆ S₂₉₈⁰ та ізобарно-ізотермічний потенціал ∆ G₂₉₈⁰ реакції (за вказаним варіантом). Зробіть висновок про можливість протікання реакції в стандартних умовах.

Реакції:

Варіант №1

Mg(OН)_2(ТВ) + ТіО (тв) MgТіO_(ТВ) + Н₂О

Варіант №2.

MgSіО_{3 (кр)} + Н₂О_(р) Mg(OН)_2(ТВ) + SіО_{2 (тв)}

Варіант №3.

Mg(OН)_2(ТВ) + 2НСІ (г) MgСІ_{2 (тв)} +2Н₂О

Варіант №4.

2NH₃ + 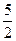О₂ 2 NО + 3Н₂О

Варіант №5.

MgO(тв) + SО₃ = MgSО_{4 (тв)}

Варіант №6.

АІО₃ (тв) + MgCО₃ (тв) MgАІ₂О₄ (тв) + СО₂

Таблиця 1.3

Термодинамічні властивості деяких речовин

Речовина	Стан	DН298 кДж/моль	DS298 Дж/моль× К
C С H2 І2 І2 H2O H2O НСl НІ CO CO2 СН4 С2Н2 С2Н4 С2Н6 С2Н5ОН СН3СООН NO NO2 SO2 SO3 SiO2 TiO2 MgO Aℓ2O3 NCℓ H2SO4 NH3 NH4С1 NaBr Na С1 KBr СаСО3 СаО Са(ОН)2 Fe(OH)2 Fe(OH)3 Fe2O3 Mg Cℓ2 Mg(ОH)2 MgSO3 MgSiO3 Mg2TiO3 Mg2SiO4 Mg2TiO4 Mg Aℓ2O4 Mg SO4	Алмаз Графіт Газ Кристал Газ Рідина Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Газ Кварц Рутил Крист. Корунд Рідина Рідина Газ Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист. Крист.	+1,9 - -286,02 - 62,47 -241,98 -241,98 -92,3 26,59 -110,6 -393,77 -74,86 266,17 52,50 -84,78 -234,75 -432,1 +90,31 +33,20 -297,05 -396,07 -911,55 -944,12 -601,64 -1676,81 -92,37 -814,33 -46,14 -314,40 -361,66 -411,39 -392,43 -1207,93 -635,51 -986,75 -562,06 -827,18 -822,7 -642,05 -925,28 -1113,69 -1594,12 -1572,14 -2177,14 -2164,58 -2307,76 -1262,61	2,38 5,21 70,13 116,23 260,77 70,40 188,95 186,92 206,62 197,7 213,78 186,44 200,97 219,43 229,65 282,60 282,60 210,79 240,11 248,28 256,82 41,87 50,28 26,96 50,95 186,92 157,00 192,47 95,90 86,88 72,16 95,92 88,80 39,77 83,44 88,00 105,00 87,5 89,69 63,22 65,73 67,78 74,58 95,17 115,22 80,68 91,44

Дата добавления: 2014-11-29