Динамическое программирование 2 страница

С помощью однофакторного дисперсионного анализа определить, является ли влияние возраста как фактора на уровень нейротизма статистически значимым.

Алгоритм решения

1.

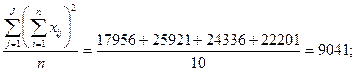
2.

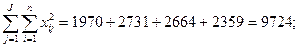
3. SS_w = (2) – (1) = 9724 – 9041 = 683;

4.

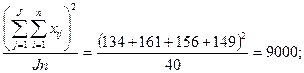
5. SS_b = (1) – (4) = 9041 – 9000 = 41;

6. SS_c = (2) – (4) = (3) + (5) = 9724 – 9000 = 683 + 41 = 724;

7.

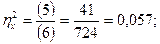
8.

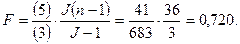
Ответ

F = 0,720 < F_кр. = 2,86. Влияние возраста как фактора на уровень нейротизма не является статистически значимым.

10. 4. Двухфакторный дисперсионный анализ

Двухфакторный дисперсионный анализ (ДДА) служит для изучения влияния на результирующий признак двух различных факторов. ДДА подразумевает формирование и анализ двухфакторных дисперсионных комплексов (ДДК).

Анализ ДДК включает в себя 5 этапов.

1. Подбор факторов:

При организации ДДК свободный выбор факторов ограничен требованием их полной независимости друг от друга.

2. Разделение факторов на градации:

При организации ДДК каждый фактор разделяется на градации с таким расчетом, чтобы для каждой градации первого фактора было подобрано одинаковое число градаций второго фактора.

В качестве примера рассмотрим ситуацию, когда в качестве факторов выступают явно независимые друг от друга свойства, такие как пол и возраст (табл. 10.7).

Таблица 10.7

Факторы	Градации
А – пол	А1 - мужчины, А2 – женщины
В – возраст	В 1– 20 ¸ 30 лет; В 2– 30 ¸ 40 лет; В 3– 40 ¸ 50 лет;
Организация комплекса
Правильная	Неправильная
A 1	A 2	A 1	A 2
B 1	B 2	B 3	B 1	B 2	B 3	B 1	B 2	B 3	B 1	B 2

3. Подбор объектов исследования:

Результаты дисперсионного анализа зависят от того, насколько правильно подобраны объекты исследования по качеству и по количеству.

По своему качеству объекты должны отражать те генеральные совокупности, для изучения которых проводится исследование.

По величине изучаемого признака объекты (испытуемые) должны быть взяты по принципу случайной выборки без учета выраженности данного признака. Измеряют и учитывают величину признака после отбора испытуемых в выборочный комплекс.

Организация дисперсионного комплекса с выполнением принципа случайности называется рандомизацией, а комплексы, организованные таким образом – рандомизированными. Нарушение принципа случайности при отборе объектов для дисперсионного анализа всегда приводит к неправильным результатам вследствие ошибки репрезентативности.

По числу объекты (испытуемые) могут быть распределены по градациям факторов различными способами - поровну, пропорционально или неравномерно. В соответствии с этим комплексы бывают равномерными, пропорциональными и неравномерными (табл. 10.8).

Таблица 10.8

Равномерные

Пропорциональные

Неравномерные

Гра-да-ции

A 1

A 2

Гра-да-ции

A 1

A 2

Гра-да-ции

A 1

A 2

B 1

B 2

B 1

B 2

B 1

B 2

B 1

B 2

B 1

B 2

B 1

B 2

N

n

n

B 1: B 2

1:1

1:1

B 1: B 2

1:3

1:3

B 1: B 2

1:1

1:3

В равномерных и пропорциональных комплексах отношение объемов градаций по второму фактору одинаково для каждой градации первого фактора. Такое распределение объектов по градациям ДДК определяет их особые ортогональные свойства. Комплексы, обладающие этими свойствами (равномерные и пропорциональные) называются ортогональными.

Работа с неравномерными комплексами достаточно трудна, а интерпретация результатов менее надежна, нежели при работе с ортогональными комплексами.

В некоторых случаях полученный неравномерный комплекс можно преобразовать в пропорциональный или равномерный рандомизированным изъятием отдельных единичных значений признака.

4. Преобразование значений результативного признака:

Для облегчения счетной работы можно неудобные для счета (или ввода в компьютер) значения результативного признака (многозначные, дробные) преобразовывать в малозначные и целые числа.

Возможны следующие преобразования:

1. Все значения признака можно разделить на одно и то же число К. Это делают тогда, когда все значения делятся на число без остатка, а также в случае перехода к новым единицам измерения. Если деление происходит без изменения единицы измерения, то в некоторые результаты надо внести соответствующие поправки: значения SS умножают на К ², а S x/n умножают на К.

2. Все значения можно умножить на одно и то же число К. Это делают, например, когда значения представлены дробными числами. Поправки в конечные результаты вносятся обратные тем, которые вносились в предыдущем случае.

3. От всех значений можно отнять одно и то же число А. Это лучше делать тогда, когда размах значений невелик и их деление или умножение на число К с последующим округлением может заметно снизить разнообразие измеряемого признака. Поправка в окончательный результат вносится только для среднего арифметического 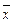(необходимо прибавить число А). Остальные значения никаких поправок не требуют.

4. Можно сделать двойное преобразование, например, из каждого значения можно вычесть число А, а полученный результат разделить (умножить) на число К.

Способы преобразования и поправки при различных типах преобразований показаны в табл. 10.9.

Таблица 10.9

Способ преобра­зования	Поправки
	SS
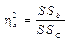
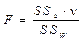
xi·K	: K	: K	: K	—	—
x i– А	+ A	—	—	—	—
(x i– A)/ K	· K + A	· K^2	· K^2	—	—
x i/ K	· K	· K^2	· K^2	—	—

Анализ двухфакторных комплексов

Анализ двухфакторных комплексов проводится в несколько этапов:

1. Расчет дисперсий (сумм квадратов). Дисперсии рассчитываются в трех однофакторных комплексах:

а) для общего комплекса (SS _b, SS _W, SS_C);

б) для первого фактора (А);

в) для второго фактора (В).

2. Анализ влияния. В ДДК анализируют 6 влияний:

а) влияние первого фактора (А);

б) влияние второго фактора (В);

в) влияние сочетаний градаций обоих факторов (АВ);

г) суммарное действие организованных (двух) факторов (А + В);

д) суммарное действие неорганизованных (остальных) факторов (случайные влияния) (W);

е) суммарное действие всех факторов, определяющих величину результирующего признака (C).

Все вышеперечисленные операции двухфакторного дисперсионного анализа можно проиллюстрировать следующим примером.

Условие задачи

На больных амнезией испытывалось действие двух лекарственных препаратов (А и В), которые, согласно предварительным испытаниям, способствуют улучшению памяти. Для первого препарата была взята контрольная группа (А ₀) и группа больных, прошедших месячный курс лечения (А ₁). Для второго препарата исследовались 3 градации больных (В ₀ – контроль, В ₁ – больные, прошедшие один курс лечения, и В ₂ – больные, прошедшие два месячных курса лечения препаратом).

Для каждой комбинации были выбраны по 5 больных, которые тестировались по методу Эббингауза (запоминание и воспроизведение бессмысленных слогов). В качестве критерия использовалась средняя вероятность правильного воспроизведения у каждого больного. Получены следующие данные (табл. 10.10):

Таблица 10.10

Пациент	Комбинации
A 0 B 0	A 0 B 1	A 0 B 2	A 0 B 0	A 0 B 1	A 0 B 2
	0,08 0,22 0,32 0,20 0,12	0,80 0,64 0,96 0,72 0,80	0,56 0,42 0,56 0,46 0,32	0,24 0,36 0,48 0,36 0,72	0,16 0,22 0,28 0,42 0,56	0,32 0,16 0,16

Задание

Методом двухфакторного дисперсионного анализа определить степень эффективности препаратов А и В, используемых для лечения больных амнезией при их раздельном и совместном применении.

Решение

1. Используем операцию x _i·100:2. Получаем следующие данные (табл. 10.11):

Таблица 10.11

Пациент	A 0 B 0	A 0 B 1	A 0 B 2	A 0 B 0	A 0 B 1	A 0 B 2

2. Рассчитываем дисперсии в общем комплексе (табл. 10.12):

Таблица 10.12

	A 0	A 1
B o	B 1	B 2	B 0	B 1	B 2
x i							J A = 2 J B = 3 n = 5
n							Jn = 30
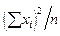
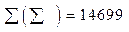
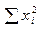
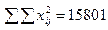
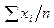
	9,4	39,2	23,2	21,6	16,4	6,4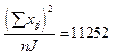

а) межгрупповая дисперсия:

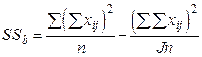= 14699 – 11252 = 3447;

б) внутригрупповая дисперсия:

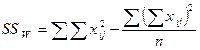= 15801 – 14699 = 1102;

в) общая дисперсия:

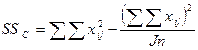= 15801 – 11252 = 4549.

3. Рассчитываем дисперсии для факторов А и В и для сочетания их градаций (АВ) (табл. 10.13):

Таблица 10.13

	Для фактора A	Для фактора B
	A 0	A 1	S	B 0	B 1	B 2	S
n

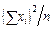
SS _A = 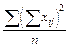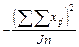= 11878 – 11252 = 626;

SS _B = 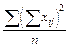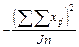= 12320 – 11252 = 1068;

SS _AB = SS _b –- SS _A – SS_B = 3447 – 626 – 1068 = 1753.

4. Проводим анализ частных средних:

А₀В₀ - контроль, А₁ - курс лечения препаратом А, В₁ - курс лечения препаратом В, В₂ - двойной курс лечения препаратом В.

А ₀: В ₀ = 9,4; B ₁ = 39,2; B ₂ = 23,2.

A ₁: B₀ = 21,6; B ₁ = 16,4; B ₂ = 6,4.

Анализ частных средних показывает, что наиболее высокий уровень воспроизведения характерен для сочетания А ₀ В ₁ (т.е. после месячного курса лечения препаратом В). Двойной курс лечения препаратом В нецелесообразен, т. к. воспроизведение снижается. Лечение препаратом А дает менее выраженный эффект, а комбинированное применение препаратов А и В вообще нецелесообразно

5. Анализ влияния(табл. 10.14).

Таблица 10.14

	SS		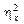n	SS/ n	F	n1 g A g B –1	n2 Jn - g A g B	F st b1; b2
A		0,14			13,61			4,3; 7,8
B		0,23			11,61			3,4; 5,6
AB (n=n A n B)		0,39			19,04			3,4; 5,6
A+B (n=g A g B -1)		0,76			14,98			2,6; 3,9
W		0,24
C		1,00

Сила влияния: 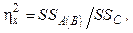где SS _C - общая дисперсия.

Достоверность влияния:

:

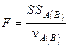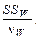
где SS _W - случайная (внутригрупповая) дисперсия.

Анализ силы влияния

- действие первого фактора (при усредненном действии второго) составляет 0,14 (14%) от действия всей суммы факторов, определяющих величину результативного признака;

- действие второго фактора (при усредненном действии первого) оказалось более сильным: 0,23 (23%);

- значительно сильнее оказалось действие сочетаний градаций обоих факторов: 0,39 (39%);

- действие первого фактора в значительной степени зависит от градации второго: максимальный эффект наблюдается при отсутствии второго, минимальный - после двух курсов лечения вторым препаратом;

- в отсутствие первого фактора максимальный эффект наблюдается после одного курса лечения вторым препаратом, после повторного курса эффект снижается.

Анализ достоверности влияния

Влияние каждого из факторов в отдельности, а также их сочетания достоверно при 1-м (b₁ = 0,95) и 2-м (b₂ = 0,99) уровнях значимости.

З а д а ч и п о т е м е

Задача 10. 1

Условие задачи

С целью определения степени эффективности сеансов НЛП, проводимых у больных неврастенией, выбрано 4 группы больных по 10 человек в каждой: первая группа - контрольная (К), в которой психотерапевтических воздействий не проводилось; вторая группа (1) – больные, прошедшие 1 сеанс НЛП; третья (2) – 2 сеанса и четвертая (3) – 3 сеанса НЛП. В качестве критерия эффективности психотерапевтического воздействия использовался уровень ситуативной тревожности (УСТ) по тесту Спилбергера. Получены следующие данные:

Группы	Уровень ситуативной тревожности
К

Задание

Определить эффективность сеансов НЛП, используя результаты тестирования по Спилбергеру на уровень ситуативной тревожности.

Задача 10. 2

Условие задачи

Группа учеников одной из школ г. Екатеринбурга была обследована по тесту Айзенка на уровень экстра-интроверсии и нейротизма. Обследование было проведено четырехкратно с перерывами в 1-2 года: в 7-м, 8-м, 9-м и 10-11-м классах. Были получены следующие результаты:

Показатель

Экстра-интроверсия

Нейротизм

№№ п.п.

Испыту- емый

7 кл.

8 кл.

9 кл.

10-11 кл.

7 кл.

8 кл.

9 кл.

10-11 кл.

Д.О. С.Н. Д.Л. Г.К. Н.А. В.Р. К.К. М.С. Р.Я. С.А.

Задание

Используя метод однофакторного дисперсионного анализа, определить, достоверно ли изменяются показатели экстра-интроверсии и нейротизма у подростков с 7 по 11 класс.

З а д а ч а 10. 3

Условие задачи

Проводилось исследование возрастной динамики личностной тревожности у подростков. Для этого были взяты 4 независимых группы испытуемых в возрасте, соответственно, 13, 14, 15 и 16 лет по 10 человек в каждой. Обследование проводилось по тесту Спилбергера – Ханина. Получены следующие результаты:

Испытуемые
Возраст
Уровень личностной тревожности в баллах
13 лет
14 “
15 “
16 “

Задание

Определить, достоверно ли изменяется уровень личностной тревожности у подростков в возрасте с 13 до 16 лет.

З а д а ч а 10. 4

Условие задачи

В психологическом эксперименте исследовалось влияние мотивации на уровень запоминания слов. Трем группам испытуемых (10 человек в каждой) были предложены 20 многосложных, редко используемых слов. Первой группе было обещано, что правильное воспроизведение десяти и более слов будет вознаграждаться призами. Во второй группе испытуемые предупреждались, что при воспроизведении менее 7 слов они будут должны сделать несколько физических упражнений. В третьей группе никаких дополнительных инструкций не давалось. Были получены следующие результаты:

	Группа	Испытуемые
Количество правильно воспроизведенных Слов

Задание: Определить, влияет ли мотивация на успешность запоминания.

З а д а ч а 10. 5

Условие задачи

Психолог проводил курс психокоррекционных занятий с целью улучшения социальной адаптации детей. Занятия проводились с шестиклассниками средней школы в возрасте 11-12 лет. До и после курса занятий проводилось тестирование по рисуночному тесту С. Розенцвейга. В качестве показателя использовался коэффициент групповой адаптации (КГА), значения которого до и после курса психокоррекции приводятся в таблице.

Школьники	КГА в %	Школьники	КГА в %
до коррекции	после коррекции	до коррекции	после коррекции
	35,3 52,9 47,1 38,2 44,1 29,4 32,4 55,7 35,3 44,1 64,7 44,1	47,1 52,9 52,9 29,4 47,1 55,7 64,7 58,8 44,1 44,1 55,7 47,1		58,8 47,1 32,4 61,8 55,7 70,6 23,5 47,1 29,4 61,8 44,1 35,3	58,8 52,9 64,7 55,7 61,8 61,8 32,4 47,1 35,3 58,8 52,9 64,7

Задание

Опираясь на данные тестирования, определить эффективность работы психолога.

З а д а ч а 10. 6

Условие задачи

Ортега и Пипал (1984) измеряли уровень диастолического давления у 20 испытуемых в трех различных условиях: в состоянии покоя, после релаксации, после 15 минут двигательной активности. Полученные данные представлены в таблице.

Испы-туемые	Актив-ность	Покой	Релакса-ция	Испы-туемые	Актив-ность	Покой	Релакса-ция

Вопрос

Влияет ли уровень активности на артериальное давление?

________________________________________________________________________________

РАЗДЕЛ 11

ЭЛЕМЕНТЫ МНОГОМЕРНОЙ СТАТИСТИКИ
11.1. Основные понятия

Методы многомерной статистики используются в тех случаях, когда необходимо упорядочить (привести в определенную систему) большое количество переменных (измеряемых свойств, признаков, характеристик, психологических свойств и т. п.). Чаще всего к многомерной статистике прибегают специалисты в области дифференциальной психологии, которая решает проблему индивидуальных психологических различий, проблему типологизации личности и т. д.

Наиболее часто в психологии используются кластерный и факторный анализ, реже – дискриминантный анализ. Каждый из них давно уже перерос из отдельных методов в самостоятельные области математической статистики. По сути, эти направления лишь условно можно назвать «статистикой» (на том основании, что они основаны на использовании стандартных статистических методов). На самом же деле это более высокий уровень – уровень математического моделирования различных психологических свойств, процессов и состояний.

Дата добавления: 2014-11-29