Динамическое программирование 3 страница

В данном разделе будут рассмотрены кластерный и факторный анализ.

11.2. Кластерный анализ

По степени использования кластерного анализа психологи, очевидно, занимают второе место (после биологов). В биологии кластерный анализ используется, в первую очередь, для создания классификационных (таксономических) схем растительного и животного мира. В психологии же кластерный анализ используется при исследовании структуры психологических свойств индивида, степени общности различных психологических характеристик, черт, признаков, характера их взаимной упорядоченности, взаимоотношений с множеством других признаков и т. д. Вполне понятно, что каждый психологический признак, свойство или черта не являются изолированными – как правило, они имеют большую или меньшую степень связи друг с другом. Для выявления этих взаимосвязей и предназначен кластерный анализ. Кластерный анализ имеет смысл проводить в тех случаях, когда регистрируется большое число переменных (по крайней мере, больше десятка разных признаков).

В математическом смысле задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся в множестве Х, разбить множество объектов I на m кластеров (подмножеств) p ₁, p ₂,..., p _m так, чтобы каждый объект I _i принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными (несходными) по выбранному критерию.

Решением задачи кластерного анализа является разбиение, удовлетворяющее некоторому критерию оптимальности (целевой функции).

Пример:

8 объектов, обладают одной характеристикой (n = 8, p = 1); результаты измерения представляют собой множество X = {3, 4, 7, 4, 3, 3, 4, 4}; целевая функция – внутригрупповая сумма квадратов отклонений, которая предполагается быть минимальной.

Тогда:

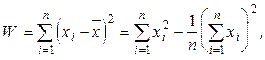(11.1)

где x _i представляет собой измерение i -го объекта.

В нашем случае: W = 140 – 128 = 12.

Если множество X разбить на 3 группы: G ₁ = {3, 3, 3}, G ₂ = {4, 4, 4, 4}, G ₃ = {7}, то все внутригрупповые суммы квадратов отклонений будут равны нулю: W ₁ + W ₂ + W ₃ = 0 + 0 + 0 = 0, где W _i обозначает сумму квадратов, соответствующую группе G_i. Оптимальное значение для этого примера равно нулю при условии, что ведется разбиение на 3 группы. В общем случае необходимо рассматривать значение целевой функции в сочетании с желаемым числом групп разбиения.

11.2.1. Функции расстояния

Для решения задачи кластерного анализа необходимо количественно определить понятия сходства и разнородности. Для этого вводится понятие расстояния (отдаленности) между соответствующими точками x_i и x_j. Если это расстояние достаточно мало, объекты i и j попадают в один кластер, если оно велико – в разные.

Используются следующие наиболее употребимые меры расстояния:

Евклидово расстояние: d ₂(X _i, X _j) = 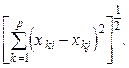(11.2)

l ₁ - норма: d ₁(X _i, X _j) = 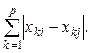(11.3)

l _р - норма: d _p(X _i, X _j) = 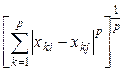(11.4)

Мера Джеффриса-Матуситы: M = 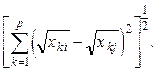(11.5)

Коэффициент дивергенции Кларка: СD = (11.6)

Существуют и другие, более сложные меры расстояния, выбор которых определяется как субъективным предпочтением исследователя, так и естественным стремлением к упрощению процедуры эксперимента.

11.2.2. Меры сходства

Как правило, в качестве меры сходства используется корреляция между рядами признаков (переменных). Объекты (признаки) считаются сходными, если коэффициент корреляции близок к +1 (положительное сходство) или к –1 (отрицательное сходство), и не сходны, если r_ij близок к нулю. В качестве граничного значения для объединения переменных в один кластер используется критическое значение коэффициента корреляции, которое находится по соответствующим таблицам.

При построении векторных моделей необходимо подчеркнуть следующее: если X _i и X _j рассматривать как координаты двух точек в многомерном пространстве, то r _ij = cos q, где q - угол между двумя векторами.

11.2.3. Выбор числа кластеров

Кластеризация полным перебором

Является наиболее прямым способом решения проблемы и заключается в полном переборе всех возможных разбиений на кластеры и отыскании такого разбиения, которое ведет к оптимальному (минимальному) значению целевой функции. Такая процедура выполнима лишь в тех случаях, когда n (число объектов) и m (число кластеров) невелико, поскольку число разбиений (W) прогрессивно возрастает с увеличением n и m (напомним, что n ³ m). Число возможных разбиений при ограниченном числе объектов и кластеров приведено в табл. 11.1.

Таблица 11.1

	n = 4	n = 5	n = 6	n = 7	n = 8
m =1
m =2
m =3
m =4

Суть методов динамического программирования состоит в целенаправленном поиске разбиения, дающего минимальное значение величины W. При этом все разбиения, которые приводят к большему значению W, отбрасываются.

Пример:

При n = 6 и m = 3, W = 90. При этом 90 альтернатив кластеризации дают 3 формы распределения:

1: {4}, {1}, {1} – 15 возможных вариантов;

2: {3}, {2}, {1} – 60 " "

3: {2}, {2}, {2} – 15 " "

Оптимальное распределение соответствует форме 3, которая и служит основой для дальнейшего перебора вариантов:

(1, 2) (3, 4) (5, 6)

(1, 3) (2, 4) (5, 6)

(1, 4) (2, 3) (5, 6) и т. д.

В процедуре динамического программирования имеются повторения сочетаний признаков в одном и том же кластере (в нашем примере (5, 6)), что в значительной мере сокращает число вычислений.

Естественно, что такой подход несколько произволен, так как минимизация числа разбиений, по сути, не означает, что именно эти распределения являются оптимальными.

Дата добавления: 2014-11-29