
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамическое программирование 1 страница
|
|
|
|
Кроме двух вышеуказанных показателей, при использовании метода наименьших квадратов часто вычисляют величину ошибки регрессии (s). Ошибка регрессии по сути является аналогом стандартного отклонения. Она отражает степень точности определения положения линейной функции в данной системе координат.
Вычисление ошибки регрессии:
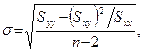 где
где 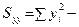
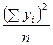 . (9.4)
. (9.4)
Величина ошибки регрессии может отражать:
а) величину разброса экспериментальных точек относительно теоретических значений функции, т.е. она тем больше, чем больше сумма квадратов отклонений от теоретической функции (при полном совпадении экспериментальных и теоретических значений s = 0);
б) нелинейность функции в данной системе координат (для определения нелинейности функции не следует пренебрегать ее графическим изображением и не следует пытаться описать уравнением линейной регрессии функцию, которая явно не является линейной).
Ошибка коэффициента уравнения линейной регрессии (тангенса угла наклона) определяется по формуле:
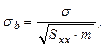
|
(9.5)
где σ – величина ошибки регрессии, m - число измерений для каждого y (при условии повторения эксперимента).
В тех случаях, когда возникает необходимость сравнить между собой две индивидуальные или усредненные функции на предмет достоверности их различий, можно использовать величины тангенса угла наклона с соответствующим доверительным интервалом: b 1 ± t× sbи b 2 ± t× sb. Вывод о достоверности различий делается в том случае, когда доверительные интервалы для двух испытуемых (или двух выборок) не перекрываются между собой (так же как и в случае определения достоверности различий между выборками по критерию Стьюдента (см. подраздел 7.4.)).
Для того чтобы приобрести определенный навык в расчетах подобного рода, рассмотрим задачу из области психофизики.
Условие задачи
В психофизических исследованиях субъективной оценки громкости (R) тонального звука, проведенных на 50 испытуемых, были получены следующие данные (табл. 9.1):
Таблица 9.1
| I, дБ | |||||||||
| R | 1,4 | 2,9 | 6,8 | 10,5 | 17,4 | 27,5 | 66,1 | 107,2 | 158,5 |
Задание
Принимая, что усредненные оценки громкости описываются степенной функцией Стивенса, с помощью метода наименьших квадратов рассчитать основные параметры психофизической функции субъективной оценки громкости.
Решение
1. Учитывая тот факт, что степенная функция Стивенса y = k · S n есть в то же время двойная логарифмическая функция типа log y = n · log S + C, и то, что шкала децибелов представляет собой логарифмическую шкалу (20 дБ = 1 лог. ед.), проводим следующие преобразования:
а) преобразуем физическую шкалу сенсорного стимула в логарифмические единицы по десятичному основанию по принципу х = I / 20.
б) логарифмируем значения субъективной шкалы по принципу y = lg R (табл. 9.2).
Таблица 9.2
| x | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 |
| y | 0,15 | 0,46 | 0,83 | 1,02 | 1,24 | 1,44 | 1,82 | 2,03 | 2,20 |
2. Вычисляем предварительные (рабочие) параметры:
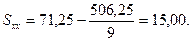
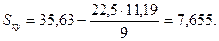
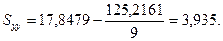
3. Вычисляем основные параметры психофизической функции:
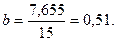
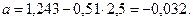
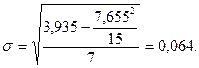
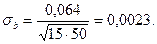
Вывод
Субъективная оценка громкости тонального звука для данной группы испытуемых описывается степенной функцией Стивенса следующего типа:
у = 0,51 х – 0,032, или R = 1,076 I 0,51 + C (антилогарифм 0,032 равен –1,076).
В некоторых случаях возникает задача сравнения между собой психофизических функций у двух или более испытуемых на предмет достоверности их различий. Попарное сравнение можно сделать, определяя тангенс угла наклона функции с доверительным интервалом. Так, различия можно считать статистически достоверными, если интервалы b 1 ± t n-1·σb1 и b 2 ± t n-1·σb2 не имеют области перекрытия.
9.4. Множественная регрессия
Предположим, что на величину исследуемого признака (y) оказывает влияние большое число разнообразных факторов:
y = a + b 1 x 1 + b 2 x 2 +... + b m x m. (9.3)
где x 1, x 2, … x m – факторы, оказывающие влияние на переменную величину. Коэффиценты при факторах по сути представляют собой коэффициенты корреляции факторов с результирующим признаком. Для определения коэффициентов b 1, b 2 ,..., b m (т. е. степени влияния факторов x 1, x 2,..., x m на параметры функции), а также свободного члена уравнения а существуют специальные алгоритмы и компьютерные программы. Расчет множественной регрессии на калькуляторе чрезвычайно громоздок, поэтому, как правило, вычисления ведутся на компьютере.
По сути дела задача множественного регрессионного анализа сводится к выявлению тех факторов, которые оказывают наиболее существенное влияние на величину исследуемого признака, и исключению тех факторов, влияние которых незначительно.
З а д а ч и п о т е м е
Задача 9. 1
Условие задачи
5 испытуемых оценивали субъективную тяжесть предлагаемых им грузов массой от 20 до 1280 г. Использовался метод категориального шкалирования (группировки), причем тяжесть каждого груза предлагалось оценить одной из пяти категорий: 1 – очень легкий, 2 – легкий груз, 3 – груз средней тяжести, 4 – тяжелый и 5 – очень тяжелый. Получены следующие результаты:
| Испытуемый | Масса груза в граммах | ||||||
Задание
По данным, усредненным по 5 испытуемых, построить психофизическую функцию категориальной оценки. Определить форму зависимости и рассчитать основные параметры функции.
Задача 9. 2
Условие задачи
Двое испытуемых визуально оценивали площадь круга в относительных единицах. Получены следующие данные:
| Площадь круга, см2 | S | |||||||||
| Оценки 1-го испытуемого | R 1 | 1,0 | 1,2 | 1,5 | 2,5 | 3,6 | ||||
| Оценки 2-го испытуемого | R 2 | 1,5 | 2,5 |
Задание
1. Методом подбора координат определить форму психофизической функции для обоих испытуемых (использовать полулогарифмические и двойные логарифмические координаты).
2. Методом наименьших квадратов рассчитать основные параметры психофизических функций (b, a, sиsb) для обоих испытуемых.
3. Используя величины b 1и b 2, определить достоверность различий между психофизическими функциями двух испытуемых (для 1-го уровня значимости t ст. = 2,31).
З а д а ч а 9. 3
Условие задачи
Шкалирование яркости светового сигнала, проведенное 50 испытуемыми, обнаружило следующие соотношения между физической яркостью (B) и ее субъективной оценкой (R B):
| B, кд/м2 | 2,5 | ||||
| Rв | 1,0 | 1,5 | 2,2 | 3,2 | 4,7 |
| B, кд/м2 | |||||
| Rв | 6,8 | 10,1 | 14,8 | 21,7 | 32,0 |
Задание
Принимая, что субъективная оценка яркости описывается степенной функцией Стивенса, построить психофизическую функцию в координатах lg R = f (lg B) и определить ее основные параметры (b, a, sиsb).
З а д а ч а 9. 4
Условие задачи
10 испытуемых оценивали длительность тонального звука методом кросс-модального подбора, рисуя линии соответствующей длины на экране дисплея. Получены следующие результаты:
| Испытуемый | Длительность звука в секундах | ||||||
| 0,25 | 0,5 | 1,0 | 2,0 | 4,0 | 8,0 | 16,0 | |
| Ю. П. Ю. М. Л. Г. И. Т. Т. З. Е. К. Н. У. М. Х. Л. К. Н. А. |
Примечание: цифры в таблице соответствуют длине подбираемых линий в миллиметрах.
Задание
1. Методом подбора координат определить форму психофизической функции L = f (T) для данных, усредненных по 10 испытуемым.
2. Методом наименьших квадратов вычислить основные параметры психофизической функции для кросс-модального подбора длины линий к длительности звукового сигнала.
РАЗДЕЛ 10
Меры влияния
10. 1. Сущность проблемы
В различных областях психологии часто приходится иметь дело с влиянием на исследуемый признак тех или иных факторов. Понятие фактора в данном случае трактуется чрезвычайно широко: по сути, это любое воздействие, которое может изменять величину исследуемого признака. Так, в клинической практике это может быть действие психотропных препаратов или психотерапевтического воздействия. В педагогической психологии в качестве факторов могут выступать те или иные учебно-воспитательные методики. При исследовании какого-либо психологического признака в разных возрастных группах в качестве фактора может рассматриваться возраст испытуемых и т. д. При влиянии определенных факторов или их совокупности величина исследуемого признака может меняться в ту или иную сторону. Задача состоит в том, чтобы на основании изменения исследуемого признака определить статистическую достоверность (значимость) влияния данного фактора. Для анализа достоверности влияния того или иного фактора, а также для сравнения между собой силы влияния разных факторов используются как параметрические (дисперсионный анализ), так и непараметрические меры влияния (критерий знаков, критерий Т Вилкоксона и др.).
10. 2. Непараметрические меры влияния
10.2.1. Критерий знаков
Критерий знаков используется в тех случаях, когда измерение психологического признака проводится на одной и той же группе (выборке) испытуемых до и после однократного воздействия интересующего нас фактора. Критерий знаков весьма прост для вычисления и предусматривает лишь установление знака различий между парами сравниваемых величин исследуемого признака до и после влияния. Суммируя число положительных и отрицательных сдвигов, находится их соотношение и сравнивается с табличным (критическим). Влияние фактора считается статистически достоверным, если расхождения значений превышают табличное значение. Если в экспериментальных данных имеются нулевые сдвиги (т. е. исследуемый признак не изменяется под воздействием фактора), то такие результаты исключаются из рассмотрения, а количество наблюдений n уменьшается на число нулевых сдвигов.
10.2.2. Критерий Вилкоксона
Аналогично критерию знаков, критерий Т Вилкоксона используется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, т. е. определяет, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом. Критерий может быть использован, если исследуемый признак измерен на шкале порядка или шкале интервалов. Объем выборки – от 5 до 50 человек.
Рассмотрим алгоритм вычислений по критерию знаков и критерию Вилкоксона на примере одной и той же задачи.
Условие задачи
У 15 пациентов неврологической клиники измерялся уровень реактивной тревожности до (x i) и после (x i’) соответствующего психотерапевтического воздействия. Получены следующие результаты (табл. 10.1):
Таблица 10.1
| Испытуемый | |||||||||||||||
| x i | |||||||||||||||
| x i ’ |
Задание
Определить эффективность психотерапевтического воздействия.
Решение
Оформляем данные в виде соответствующей таблицы (табл. 10.2):
Таблица 10.2
| xi | xi’ | S | xi - xi’ | |xi - xi’|* | R | R* | R+ |
| + + – + – + – + + + + + + + – | – 2 – 1 – 4 – 1 | 2,5 2,5 2,5 2,5 14,5 14,5 | 2,5 2,5 | ||||
| Σ |
В столбце 1 таблицы приведены значения УРТ до психотерапевтического воздействия, в столбце 2 – после такового. Значения УРТ в 1-м и и 2-м столбцам должны располагаться в одном и том же порядке, т. е. каждая пара показателей соответствует одному и тому же субъекту.
Используем критерий знаков:
1. Для нахождения знака разницы (s) между xi и xi’ обозначим позитивные сдвиги (уменьшение значения признака) плюсом, а негативные (увеличение значения) – минусом (столбец 3 таблицы).
2. Находим соотношение плюсовых и минусовых значений: n (–) = 4; n (+)= 11. Таким образом, s = 4: 11 (для удобства сравнения с табличными значениями на первое мето ставится меньшее, на второе - большее число.
3. Сравниваем полученные значения с табличными (критическими) (табл. XVII Приложений): для n = 15 sкр. = 4: 11.
4. Делаем вывод о том, что по критерию знаков влияние фактора находится на границе статистической достоверности.
Таким образом, по критерию знаков мы не смогли доказать, что влияние фактора является статистически значимым даже для 1-го уровня.
При отсутствии соответствующей таблицы, можно воспользоваться формулой следующего вида:
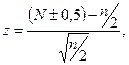 (10.1)
(10.1)
где N – сумма плюсов или сумма минусов, n - общее число значений, 0,5 - поправочный коэффициент, который добавляют к N, если N < n /2, или вычитают, если N > n /2.
Критическое значение z (мера Пирсона) для соответствующего уровня значимости находится в соответствующих таблицах.
Используем критерий Вилкоксона:
1. Находим частные разности между значениями x iи x i’ (столбец 4).
2. Выстраиваем разности в ранжированный ряд без учета знака (столбец 5).
3. Преобразуем интервальную шкалу значений в ранговую (порядковую) (столбец 6). Данная процедура не отличается от таковой при использовании критерия Манна-Уитни (см. подраздел 7.3).
4. Вводим поправки на связанные ранги (столбец 7).
5. В последний столбец (8) переносим ранговые числа переменных того знака, которых меньше (в данном случае – ранги минусовых значений).
6. Вычисляем критерий Вилкоксона, который соответствует сумме значений в столбце 8: T = Σ R –= 23.
7. В таблице критических значений (табл. XVIII Приложений) для n = 15 находим: Т кр. = 30 (для β1 = 0,95) и Т кр. = 19 (для β2 = 0,99).
Необходимо помнить, что влияние фактора считается статистически значимым, если T < T кр (аналогично критерию Манна-Уитни).
Вывод
Влияние исследуемого фактора (сеансов психотерапевтического воздействия) является статистически достоверным для 1-го уровня значимости.
10.3. Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ (ОДА) является достаточно информативным метрическим методом оценки влияния. Используется в тех случаях, когда требуется изучить однократное или повторное действие одного фактора. Говоря о повторном действии фактора, имеется в виду, что фактор представлен несколькими градациями, т. е. имеет 1, 2, 3,..., J уровней (например, повторный курс лечения психотропным препаратом, повторные сеансы психокоррекции и т. д.).
Для проведения дисперсионного анализа не обязательно проводить измерения на одной и той же выборке, т. е. нет необходимости подвергать одних и тех же субъектов влиянию всех исследуемых градаций фактора. Напротив, для каждого из J уровней (градаций фактора) берется n независимых наблюдений. Естественно, что при таком подходе принимается целый ряд допущений, иногда достаточно произвольных. Предполагается, в частности, что n наблюдений на каждом уровне независимы друг от друга и взяты из нормальной совокупности с дисперсией s2. Предполагается также, что дисперсия s2 одинакова на всех J уровнях (гипотеза однородности, или гомоскедактичности).
Однофакторный дисперсионный анализ включает в себя ряд этапов.
1. Результаты эксперимента представляются в виде следующей таблицы (двумерного массива) (табл. 10.3):
Таблица 10.3
| Условия опыта (градации фактора) | |||||
| ... | J | ||||
| X 11 | x 12 | x 13 | ... | x 1 J | |
| Повторные | X 21 | x 22 | x 23 | ... | x 2 J |
| наблюдения | . | . | . | ... | . |
| . | . | . | ... | . | |
| . | . | . | ... | . | |
| xn1 | xn2 | xn3 | ... | xnJ |
2. Для каждой выборки испытуемых определяется случайная (внутригрупповая) дисперсия SS W, связанная с вариабельностью переменной внутри каждой градации фактора:
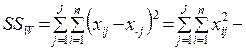
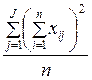 . (10.2)
. (10.2)
3. Вычисляется факториальная (межгрупповая) дисперсия SSb, связанная с влиянием градаций фактора:
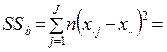
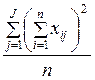
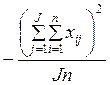 . (10.3)
. (10.3)
4. Вычисляется общая дисперсия SS c, которая соответствует сумме внутригрупповой и межгрупповой дисперсий: SS c = SS b + SS W. Общую дисперсию можно также вычислить по следующей формуле:
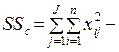
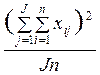 . (10.4)
. (10.4)
5. Вычисляется показатель силы влияния 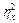 как отношение межгрупповой дисперсии к общей:
как отношение межгрупповой дисперсии к общей:
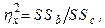 (10.5)
(10.5)
6. Определяется число степеней свободы:
а) число степеней свободы, связанное с межгрупповой дисперсией: n1 = J - 1;
б) число степеней свободы, связанное с внутригрупповой дисперсией: n2 = J (n - 1).
7. Вычисляется показатель достоверности влияния:
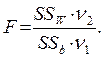 (10.6)
(10.6)
Достоверность определяется по критерию Фишера для определенного уровня значимости по соответствующей таблице. Стандартное значение F ст. определяется на перекресте столбца, соответствующего значению n1 и строки, соответствующей значению n2. Вывод о том, что влияние фактора статистически значимо, принимается, если F ³ F ст.
Для удобства работы с переменными рекомендуется пользоваться рабочей таблицей представления данных (табл. 10.4):
Таблица 10.4
| ... | J | ... | J | ||||
| x 11 x 21 . . . x n1 | x 12 x 22 . . . x n2 | ... ... ... ... ... ... | x 1J x 2J . . . x nJ | x 112 x 212 . . . x n12 | x 122 x 222 . . . x n22 | ... ... ... ... ... ... | x 1J2 x 2J2 . . . x nJ2 |
Для вычисления промежуточных значений удобно пользоваться таблицей следующего вида (табл. 10.5):
Таблица 10.5
| №№ | Вычисляемый параметр | Последовательность вычислений |
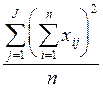
| xi (левая часть рабочей таблицы) суммируются по каждому столбцу и возводятся в квадрат: (x 11 + x 21 +... + x n1)2 (x 12 + x 22 +... + x n2)2 .............. .............. .............. (x 1J + x 2J +... + x nJ)2 Полученные квадраты суммируются и делятся на n. | |
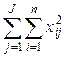
| Суммируются по столбцам квадраты чисел в правой части таблицы; полученные суммы квадратов суммируются построчно:
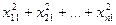 +
+
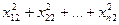 +
.............
+
+
.............
+
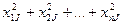
| |
| SS W = (2) – (1) | Из результата (2) вычитается результат (1), получается внутригрупповая дисперсия SS W. | |
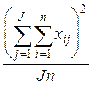
| Суммируются все варианты по столбцам и по строкам, возводятся в квадрат и делятся на общее число значений Jn. | |
| SS b = (1) – (4) | Из результата (1) вычитается результат (4), получается межгрупповая дисперсия SS b | |
| SSC = (2) – (4) = (3) + (5) | Общую дисперсию SS Cможно получить двумя путями - либо вычитанием результата (4) из результата (2), либо суммированием результатов (3) и (5), т. е. межгрупповой и внутригрупповой дисперсией. | |
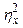 = (5)/(6) = (5)/(6)
| Показатель силы влияния вычисляется как отношение результатов (5) и (6), т.е. как отношение межгрупповой дисперсии к общей. | |
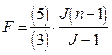
| Вычисляется отношение (5)/(3) и умножается на J (n -1)/(J -1), получается показатель достоверности влияния. |
Рассмотрим алгоритм вычислений на примере конкретной задачи.
Условие задачи
Исследовалось влияние возраста как фактора на уровень нейротизма, определяемого по тесту Айзенка. Тестирование проводилось в 4-х группах испытуемых разного возраста (соответственно, 7-й, 8-й, 9-й и 10-й классы) по 10 человек в каждой группе.
Получены следующие результаты (табл. 10.6):
Таблица 10.6
| Градации фактора | ||||||||
| Значения переменных | Квадраты значений переменных | |||||||
| Классы | 7-й | 8-й | 9-й | 10-й | 7-й | 8-й | 9-й | 10-й |
| Индивидуальные значения | ||||||||
| Σ | ||||||||
| (Σ)2 |
Задание
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 836; Нарушение авторских прав?; Мы поможем в написании вашей работы!