
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерий Стьюдента 2 страница
|
|
|
|
Пример
Пусть xi и yi – два признака, измеренные на одной и той же выборке испытуемых. Для вычисления коэффициента Фехнера необходимо вычислить средние значения для каждого признака, а также для каждого значения переменной – знак отклонения от среднего (табл. 8.1):
Таблица 8.1
| xi | yi | 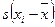
| 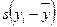
| Обозначение | |
| + - + - - + + - - + | + - - + + - - + - + | а a b b b b b b a a | |||
| Среднее | 15,5 | 17,2 |
В таблице: а – совпадения знаков, b – несовпадения знаков; n a – число совпадений, n b – число несовпадений (в данном случае n a = 4, n b = 6).
Коэффициент корреляции Фехнера вычисляется по формуле:
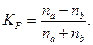 (8.1)
(8.1)
В рассматриваемом случае:
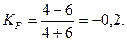
Вывод
Между исследуемыми переменными существует слабая отрицательная связь.
Необходимо отметить, что коэффициент корреляции Фехнера не является достаточно строгим критерием, поэтому его можно использовать лишь на начальном этапе обработки данных и для формулировки предварительных выводов.
8. 4. Коэффициент корреляции Пирсона
Исходный принцип коэффициента корреляции Пирсона – использование произведения моментов (отклонений значения переменной от среднего значения):
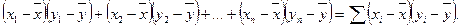 (8.2)
(8.2)
Если сумма произведений моментов велика и положительна, то х и у связаны прямой зависимостью; если сумма велика и отрицательна, то х и у сильно связаны обратной зависимостью; наконец, в случае отсутствия связи между x и у сумма произведений моментов близка к нулю.
Для того чтобы статистика не зависела от объема выборки, берется не сумма произведений моментов, а среднее значение. Однако деление производится не на объем выборки, а на число степеней свободы n - 1.
Величина 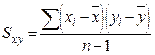 является мерой связи между х и у и называется ковариацией х и у.
является мерой связи между х и у и называется ковариацией х и у.
Во многих задачах естественных и технических наук ковариация является вполне удовлетворительной мерой связи. Ее недостатком является то, что диапазон ее значений не фиксирован, т. е. она может варьировать в неопределенных пределах.
Для того чтобы стандартизировать меру связи, необходимо избавить ковариацию от влияния стандартных отклонений. Для этого надо разделить Sxy на s x и s y:
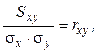 (8.3)
(8.3)
где rxy - коэффициент корреляции, или произведение моментов Пирсона.
Общая формула для вычисления коэффициента корреляции выглядит следующим образом:
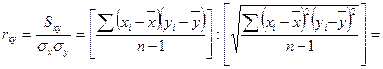
 (некоторые преобразования)
(некоторые преобразования)
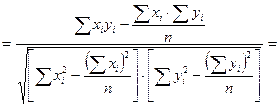
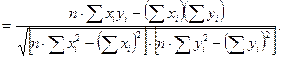 (8.4)
(8.4)
Влияние преобразования данных на r xy:
1. Линейные преобразования x и y типа bx + a и dy + c не изменят величину корреляции между x и y.
2. Линейные преобразования x и y при b < 0, d > 0, а также при b > 0 и d < 0 изменяют знак коэффициента корреляции, не меняя его величины.
Достоверность (или, иначе, статистическая значимость) коэффициента корреляции Пирсона может быть определена разными способами:
По таблицам критических значений коэффициентов корреляции Пирсона и Спирмена (см. Приложение, табл. XIII). Если полученное в расчетах значение r xyпревышает критическое (табличное) значение для данной выборки, коэффициент Пирсона считается статистически значимым. Число степеней свободы в данном случае соответствует n – 2, где n – число пар сравниваемых значений (объем выборки).
По таблице XV Приложений, которая озаглавлена «Количество пар значений, необходимое для статистической значимости коэффициента корреляции». В данном случае необходимо ориентироваться на коэффициент корреляции, полученный в вычислениях. Он считается статистически значимым, если объем выборки равен или превышает табличное число пар значений для данного коэффициента.
По коэффициенту Стьюдента, который вычисляется как отношение коэффициента корреляции к его ошибке:
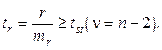 (8.5)
(8.5)
Ошибка коэффициента корреляциивычисляется по следующей формуле:
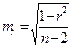 |
(8.6)
где m r - ошибка коэффициента корреляции, r - коэффициент корреляции; n - число сравниваемых пар.
Рассмотрим порядок вычислений и определение статистической значимости коэффициента корреляции Пирсона на примере решения следующей задачи.
Условие задачи
22 старшеклассника были протестированы по двум тестам: УСК (уровень субъективного контроля) и МкУ (мотивация к успеху). Получены следующие результаты (табл. 8.2):
Таблица 8.2
| №№ | УСК (xi) | МкУ (yi) | №№ | УСК (xi) | МкУ (yi) |
Задание
Проверить гипотезу о том, что для людей с высоким уровнем интернальности (балл УСК) характерен высокий уровень мотивации к успеху.
Решение
1. Используем коэффициент корреляции Пирсона в следующей модификации (см. формулу 8.4):
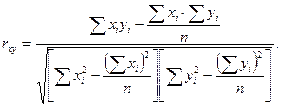
Для удобства обработки данных на микрокалькуляторе (в случае отсутствия необходимой компьютерной программы) рекомендуется оформление промежуточной рабочей таблицы следующего вида (табл. 8.3):
Таблица 8.3
| x i | y i | x i2 | y i2 | x i y i |
| x 1 x 2 x 3 . . . x n | y 1 y 2 y 3 . . . y n | x 12 x22 x 32 . . . x n2 | y 12 y 22 y 32 . . . y n2 | x 1 y 1 x 2 y 2 x 3 y 3 . . . x n y n |
| Σ x i | Σ y i | Σ x i2 | Σ y i2 | Σ x i y i |
2. Проводим вычисления и подставляем значения в формулу:
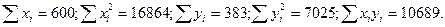
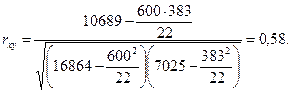
3. Определяем статистическую значимость коэффициента корреляции Пирсона тремя способами:
1-й способ:
В табл. XIII Приложений находим критические значения коэффициента для 1-го и 2-го уровней значимости: rкр. = 0,42; 0,54 (ν = n – 2 = 20).
Делаем вывод о том, r xy > r кр. , т. е. корреляция является статистически значимой для обоих уровней.
2-й способ:
Воспользуемся табл. XV, в которой определяем число пар значений (число испытуемых), достаточное для статистической значимости коэффициента корреляции Пирсона, равного 0,58: для 1-го, 2-го и 3-го уровней значимости оно составляет, соответственно, 12, 18 и 28.
Отсюда мы делаем вывод о том, что коэффициент корреляции является значимым для 1-го и 2-го уровня, но «не дотягивает» до 3-го уровня значимости.
3-й способ:
Вычисляем ошибку коэффициента корреляции и коэффициент Стьюдента как отношение коэффициента Пирсона к ошибке:
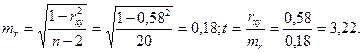
В табл. X находим стандартные значения коэффициента Стьюдента для 1-го, 2-го и 3-го уровней значимости при числе степеней свободы ν = n – 2 = 20: tкр. = 2,09; 2,85; 3,85.
Общий вывод
Корреляция между показателями тестов УСК и МкУ является статистически значимой для 1-го и 2-го уровней значимости.
Примечание:
При интерпретации коэффициента корреляции Пирсона необходимо учитывать следующие моменты:
1. Коэффициент Пирсона может использоваться для различных шкал (шкала отношений, интервальная или порядковая) за исключением дихотомической шкалы.
2. Корреляционная связь далеко не всегда означает связь причинно-следственную. Другими словами, если мы нашли, предположим, положительную корреляцию между ростом и весом у группы испытуемых, то это вовсе не означает, что рост зависит от веса или наоборот (оба этих признака зависят от третьей (внешней) переменной, каковая в данном случае связана с генетическими конституциональными особенностями человека).
3. r xu» 0 может наблюдаться не только при отсутствии связи между x и y, но и в случае сильной нелинейной связи (рис. 8.2 а). В данном случае отрицательная и положительная корреляции уравновешиваются и в результате создается иллюзия отсутствия связи.
4. rxy может быть достаточно мал, если сильная связь между х и у наблюдается в более узком диапазоне значений, чем исследуемый (рис. 8.2 б).
5. Объединение выборок с различными средними значениями может создавать иллюзию достаточно высокой корреляции (рис. 8.2 в).
y i y i y i
| .. .. .. .. .. . | ... . . . . . ... | .. ... + +.. + + + + + |
x i x i x i
а б в
Рис. 8.2. Возможные источники ошибок при интерпретации величины коэффициента корреляции (объяснения в тексте (пункты 3 – 5 примечания))
8. 5. Коэффициент ранговой корреляции Спирмена
Коэффициент корреляции Спирмена (rs) используется в тех случаях, когда оба ряда переменных представлены ранговыми (порядковыми) шкалами. Для вычисления коэффициента Спирмена можно пользоваться двумя разными формулами, которые дают, в принципе, один и тот же результат:
1) 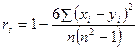 ; (8.7)
; (8.7)
2) 
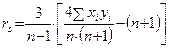 . (8.8)
. (8.8)
Коэффициенткорреляции Спирмена, так же как и rxy, может варьировать от –1 до +1. rs = 1 только в том случае, когда ранги обоих признаков в точности совпадают по х и у.
При расчете коэффициента Спирмена вручную (на микрокалькуляторе) рекомендуется использовать рабочую таблицу для промежуточных вычислений, которая имеет следующий вид:
| x i | y i | x i – y i | (x i – y i)2 | x i y i |
| x 1 x 2 . . . x n | y 1 y 2 . . . y n | x 1 – y 1 x 2 – y 2 . . . x n – y n | (x 1 – y 1)2 (x 2 – y 2)2 . . . (x n – y n)2 | x 1 y 1 x 2 y 2 . . . x n y n |
| Σ x i | Σ y i | Σ(x i – y i) | Σ(x i – y i)2 | Σ x i y i |
В зависимости от выбора формулы можно использовать столбцы 1 ¸ 4 либо 1, 2, 5.
Если в рядах переменных (или хотя бы в одном из них) имеются связанные (повторяющиеся) ранги, то следует пользоваться формулой (8.7) с соответствующей поправкой на связанные ранги:
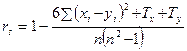 (8.9)
(8.9)
где T x = (N x3 – N x):12 и T y = (N y3 – N y):12 (N x и N y, соответственно, число связанных рангов в ряду x и в ряду y).
Статистическая значимость коэффициента ранговой корреляции Спирмена определяется аналогично значимости коэффициента корреляции Пирсона (табл. XIII, XV и X Приложений).
Рассмотрим порядок расчета коэффициента Спирмена на примере следующей задачи.
Условие задачи
12 учащихся были проранжированы психологом по их открытой неприязни к преподавателю (x i) и к другим учащимся (y i). Результаты экспертной оценки приведены ниже (табл. 8.4):
Таблица 8.4
| №№ Исп. | ||||||||||||
| xi | ||||||||||||
| yi |
Задание
Определить, существует ли связь между открытой неприязнью учащихся к преподавателю и к другим учащимся.
Решение
Составляем рабочую таблицу для вычисления коэффициента корреляции Спирмена (табл. 8.5) и вносим полученные результаты в соответствующие формулы:
Таблица 8.5
| x i | y i | (x i – y i)2 | x i y i |
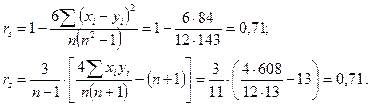 132 132
| |||
| Σ |
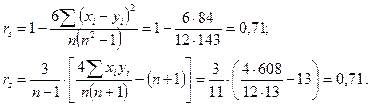 |
В таблице критических значений коэффициентов корреляции Пирсона и Спирмена находим: rкр = 0,58 (β1 = 0,95); 0,71 (β2 = 0,71).
Вывод
Корреляция является статистически значимой для 1-го уровня.
8.6. Коэффициент ранговой корреляции Кендалла
(тау Кендалла, t)
Коэффициент корреляции Кендалла используется в случае, когда переменные представлены двумя порядковыми шкалами при условии, что связанные ранги отсутствуют. Вычисление коэффициента Кендалла связано с подсчетом числа совпадений и инверсий. Рассмотрим эту процедуру на примере предыдущей задачи.
Алгоритм решения задачи следующий:
1. Переоформляем данные табл. 8.5 таким образом, чтобы один из рядов (в данном случае ряд x i) оказался ранжированным. Другими словами, мы переставляем пары x и y в нужном порядке ивносим данные в столбцы 1 и 2 табл. 8.6.
Таблица 8.6
| xi | yi | Совп. | Инв. |
| Σ |
2. Определяем «степень ранжированности» 2-го ряда (y i). Эта процедура проводится в следующей последовательности:
а) берем первое значение неранжированного ряда «3». Подсчитываем количество рангов ниже данного числа, которые больше сравниваемого значения. Таких значений 9 (числа 6, 7, 4, 9, 5, 11, 8, 12 и 10). Заносим число 9 в столбец «совпадения». Затем подсчитываем количество значений, которые меньше трех. Таких значений 2 (ранги 1 и 2); вносим число 2 в графу «инверсии».
б) отбрасываем число 3 (мы с ним уже поработали) и повторяем процедуру для следующего значения «6»: число совпадений равно 6 (ранги 7, 9, 11, 8, 12 и 10), число инверсий – 4 (ранги 1, 2, 4 и 5). Вносим число 6 в графу «совпадения», а число 4 – в графу «инверсии».
в) аналогичным образом процедура повторяется до конца ряда; при этом следует помнить, что каждое «отработанное» значение исключается из дальнейшего рассмотрения (подсчитываются только ранги, которые лежат ниже данного числа).
Примечание
Для того чтобы не совершать ошибок в подсчетах, следует иметь в виду, что с каждым «шагом» сумма совпадений и инверсий уменьшается на единицу; это понятно, если учесть, что каждый раз одно значение исключается из рассмотрения.
3. Подсчитывается сумма совпадений (Р) и сумма инверсий (Q); данные вносятся в одну и трех взаимозаменяемых формул коэффициента Кендалла (8.10). Проводятся соответствующие вычисления.
t 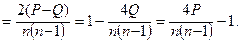 (8.10)
(8.10)
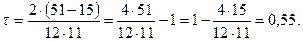 В нашем случае:
В нашем случае:
В табл. XIV Приложений находятся критические значения коэффициента для данной выборки: τкр. = 0,45; 0,59. Эмпирически полученное значение сравнивается с табличным.
Вывод
τ = 0,55 > τкр. = 0,45. Корреляция статистически значима для 1-го уровня.
Примечание:
При необходимости (например, при отсутствии таблицы критических значений) статистическая значимость t Кендалла может быть определена по формуле следующего вида:
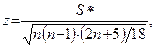 (8.11)
(8.11)
где S* = P – Q + 1, если P < Q, и S* = P – Q – 1, если P > Q.
Значения z для соответствующего уровня значимости соответствуют мере Пирсона и находятся по соответствующим таблицам (в приложение не включены. Для стандартных уровней значимости z кр = 1,96 (для β1 = 0,95) и 2,58 (для β2 = 0,99). Коэффициент корреляции Кендалла является статистически значимым, если z > z кр
В нашем случае S* = P – Q – 1 = 35 и z = 2,40, т. е. первоначальный вывод подтверждается: корреляция между признаками статистически достоверна для 1-го уровня значимости.
8.7. Дихотомический коэффициент корреляции (j)
Коэффициент j используется в качестве меры связи в тех случаях, когда признаки х и у измеряются в дихотомической шкале наименований и могут принимать значения 0 или 1. Рассмотрим способы вычислений коэффициента на пример задачи.
Условие
Проведен социологический опрос, касающийся отношения населения к религии. Было опрошено 250 респондентов (100 мужчин и 150 женщин). По результатам опроса оказалось, что среди мужчин 40 верующих и 60 атеистов, а среди женщин 85 оказались верующими и 65 – атеистами.
Задание
Определить, существует ли связь между полом и отношением к религии. Определить знак и статистическую значимость коэффициента корреляции.
Решение
Введем необходимые обозначения:
- шкала х – пол (1 – мужчины, 0 – женщины);
- шкала у – отношение к религии (1 – верующий, 0 – атеист).
Задачу можно решить двумя различными способами:
1-й способ:
1. Составляем матрицу сопряженности признаков следующего вида:
| Признак х | ||||
| Σ | ||||
| Признак у | a | b | a + b | |
| с | d | c + d | ||
| Σ | a + c | b + d |
2. Подставляем в матрицу полученные экспериментальные значения. В данном случае в качестве измеряемого признака служит число испытуемых, принимающее разные значения при сочетании шкал х и у. Так, в клетку а матрицы вносится число испытуемых, имеющих единицу по обеим шкалам, т. е число верующих мужчин; в клетку b – испытуемые, имеющие 0 по шкале х и 1 по шкале у (число верующих женщин) и т. д.
| Признак х | ||||
| Σ | ||||
| Признак у | ||||
| Σ |
3. Используем формулу дихотомического коэффициента корреляции:
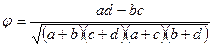 (8.12)
(8.12)
4. Проводим вычисления:
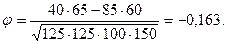
Интерпретация знака коэффициента корреляции состоит в том, что если он положителен, то 1 по х коррелирует с 1 по у, 0 по х коррелирует с 0 по у. Отрицательный коэффициент (как в нашем случае) свидетельствует о том, что 1 по х коррелирует с 0 по у, 0 по х коррелирует с 1 по у. Другими словами, женщины являются более верующими, а мужчины – более атеистичными.
По таблице критических значений дихотомического коэффициента корреляции (см. Приложение, табл. XVI) находим, что коэффициент является статистически значимым для 1-го уровня (φкр. = 0,13).
При отсутствии соответствующей таблицы можно воспользоваться следующим соотношением (для 1-го уровня значимости): 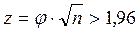 и
и 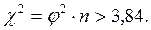
В нашем случае: z = 2,58 и χ2 = 6,64, т. е. вывод подтверждается.
Кроме того, в табл. VI Приложения можно определить статистическую значимость χ2 и для более высоких уровней (ν =1).
Вывод
Корреляция между полом и отношением к религии является статистически значимой, что можно констатировать с вероятностью 0,95.
2-й способ:
Обозначим: p x – относительная доля испытуемых, имеющих единицу по х, qx = 1 – px – имеющих нуль по х; аналогично: p y – доля испытуемых, имеющих единицу по у, qy = 1 – py – имеющих нуль по у; наконец, p xy - доля людей, имеющих единиц по x и по y.
Коэффициент j вычисляется по формуле:
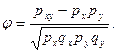 (8.13)
(8.13)
В нашем примере: p x = 100:250 = 0,40; q x = 1 – 0,40 = 0,60; p y = 120:250 = 0,50; qy = 1 – 0,50 = 0,50; p xy = 40:250 = 0,16. Подставляя значения в формулу, получаем: φ = –0,163. Вывод подтверждается.
8. 8. Точечный бисериальный коэффициент корреляции (r pb)
Точечный бисериальный коэффициент корреляции используется тогда, когда одна переменная формирует дихотомическую шкалу наименований, другая – шкалу интервалов или шкалу отношений. Порядок вычислений коэффициента рассмотрим на примере следующей задачи.
Условие задачи
В группе испытуемых, протестированных по тесту Айзенка, обнаружено 15 экстравертов, из них 8 с высоким уровнем нейротизма (холерики) и 7 – с низким нейротизмом (сангвиники). Тест Спилбергера обнаружил у тех и других следующий уровень личностной тревожности (УЛТ):
Таблица 8.7
| Тип темперамента | Уровень личностной тревожности | |||||||
| Холерики | ||||||||
| Сангвиники |
Задание
Определить уровень связи и ее статистическую значимость между типом темперамента и уровнем личностной тревожности.
Решение
1. Учитывая, что шкала типов темперамента дихотомическая, а шкала УЛТ – интервальная, используем формулу для вычисления точечно-бисериальный коэффициент корреляции:
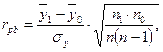 (8.14)
(8.14)
где 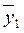 и
и 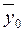 , соответственно, средние значения переменных для двух интервальных шкал, т. е. средние значения УЛТ для холериков (
, соответственно, средние значения переменных для двух интервальных шкал, т. е. средние значения УЛТ для холериков (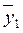 )и сангвиников (
)и сангвиников (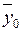 ); σу – стандартное отклонение для всей выборки; n 1 и n 0 – численность каждой из сравниваемых выборок и n = n 1 + n 0 – общее число испытуемых.
); σу – стандартное отклонение для всей выборки; n 1 и n 0 – численность каждой из сравниваемых выборок и n = n 1 + n 0 – общее число испытуемых.
2. Определяем промежуточные значения: 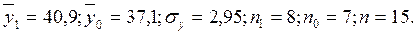
3. Проводим вычисления:
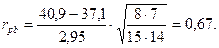
4. Определяем число степеней свободы: ν = (n 1 – 1) + (n 0 – 1) = 13.
5. В табл. XIII Приложений находим критические значения коэффициента корреляции (специальной таблицы для r pbне существует): r кр. = 0,51 (β1 = 0,95) и 0,64 (β2 = 0,99). r pb > r кр. . В данном случае можно воспользоваться и табл. XV: как можно видеть, для статистической значимости коэффициента, равного 0,67, достаточно 9 испытуемых для 1-го и 13 – для 2-го уровня (в нашем примере n = 15).
Вывод
Корреляция между типом темперамента и уровнем личностной тревожности статистически значима для 1-го и 2-го уровней.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1432; Нарушение авторских прав?; Мы поможем в написании вашей работы!