Критерий Стьюдента 1 страница

В отличие от критериев Розенбаума и Манна-Уитни критерий t Стьюдента является параметрическим, т. е. основан на определении основных статистических показателей – средних значений в каждой выборке (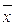 и 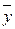) и их дисперсий (s²_x и s²_y), рассчитываемых по стандартным формулам (см. раздел 5).

Использование критерия Стьюдента предполагает соблюдение следующих условий:

1. Распределения значений для обеих выборок должны соответствовать закону нормального распределения (см. раздел 6).

2. Суммарный объем выборок должен быть не менее 30 (для β₁ = 0,95) и не менее 100 (для β₂ = 0,99).

3. Объемы двух выборок не должны существенно отличаться друг от друга (не более чем в 1,5 ÷ 2 раза).

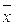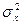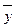Идея критерия Стьюдента достаточно проста. Предположим, что значения переменных в каждой из выборок распределяются по нормальному закону, т. е. мы имеем дело с двумя нормальными распределениями, отличающимися друг от друга по средним значениям и дисперсии (соответственно и , и 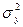, см. рис. 7.1).

s _x 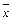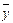s _y

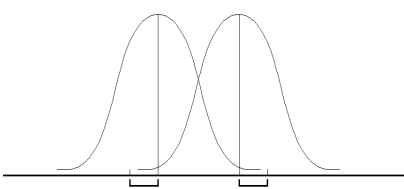
Рис. 7.1. Оценка различий между двумя независимыми выборкам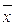и: и 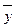- средние значения выборок x и y; s_xи s_y- стандартные отклонения

Нетрудно понять, что различия между двумя выборками будут тем больше, чем больше разность между средними значениями и чем меньше их дисперсии (или стандартные отклонения).

В случае независимых выборок коэффициент Стьюдента определяют по формуле:

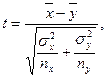(7.2)

где n _x и n _y – соответственно численность выборок x и y.

После вычисления коэффициента Стьюдента в таблице стандартных (критических) значений t (см. Приложение, табл. Х) находят величину, соответствующую числу степеней свободы n = n _x + n _y– 2, и сравнивают ее с рассчитанной по формуле. Если t _эксп. £ t _кр., то гипотезу о достоверности различий между выборками отвергают, если же t _эксп. > t _кр., то ее принимают. Другими словами, выборки достоверно отличаются друг от друга, если вычисленный по формуле коэффициент Стьюдента больше табличного значения для соответствующего уровня значимости.

В рассмотренной нами ранее задаче вычисление средних значений и дисперсий дает следующие значения: x _ср. = 38,5; σ_х² = 28,40; у _ср. = 36,2; σ_у² = 31,72.

Можно видеть, что среднее значение тревожности в группе девушек выше, чем в группе юношей. Тем не менее эти различия настолько незначительны, что вряд ли они являются статистически значимыми. Разброс значений у юношей, напротив, несколько выше, чем у девушек, но различия между дисперсиями также невелики.

Подставляем значения в формулу: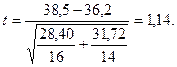

Вывод

t _эксп. = 1,14 < t _кр. = 2,05 (β₁ = 0,95). Различия между двумя сравниваемыми выборками не являются статистически достоверными. Данный вывод вполне согласуется с таковым, полученным при использовании критериев Розенбаума и Манна-Уитни.

Другой способ определения различий между двумя выборками по критерию Стьюдента состоит в вычислении доверительного интервала стандартных отклонений. Доверительным интервалом называется среднеквадратичное (стандартное) отклонение, деленное на корень квадратный из объема выборки и умноженное на стандартное значение коэффициента Стьюдента для n – 1 степеней свободы (соответственно, 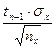и ).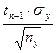

Примечание

Величина 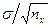= m_x называется среднеквадратичной ошибкой (см. раздел 5). Следовательно, доверительный интервал есть среднеквадратичная ошибка, умноженная на коэффициент Стьюдента для данного объема выборки, где число степеней свободы ν = n – 1, и заданного уровня значимости.

Две независимые друг от друга выборки считаются достоверно различающимися, если доверительные интервалы для этих выборок не перекрываются друг с другом. В нашем случае мы имеем для первой выборки 38,5 ± 2,84, для второй 36,2 ± 3,38.

Следовательно, случайные вариации x_i лежат в диапазоне 35,66 ¸ 41,34, а вариации y_i – в диапазоне 32,82 ¸ 39,58. На основании этого можно констатировать, что различия между выборками x и y статистически недостоверны (диапазоны вариаций перекрываются друг с другом). При этом следует иметь в виду, что ширина зоны перекрытия в данном случае не имеет значения (важен лишь сам факт перекрытия доверительных интервалов).

Метод Стьюдента для зависимых друг от друга выборок (например, для сравнения результатов, полученных при повторном тестировании на одной и той же выборке испытуемых) используют достаточно редко, поскольку для этих целей существуют другие, более информативные статистические приемы (см. раздел 10). Тем не менее, для данной цели в первом приближении можно использовать формулу Стьюдента следующего вида:

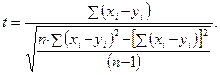(7.3)

Полученный результат сравнивают с табличным значением для n – 1 степеней свободы, где n – число пар значений x и y. Результаты сравнения интерпретируются точно так же, как и в случае вычисления различий между двумя независимыми выборками.

7.5. Критерий Фишера

Критерий Фишера (F) основан на том же принципе, что и критерий Стьюдента, т. е. предполагает вычисление средних значений и дисперсий в сравниваемых выборках. Чаще всего используется при сравнении между собой неравноценных по объему (разных по численности) выборок. Критерий Фишера является несколько более жестким, чем критерий Стьюдента, а потому более предпочтителен в тех случаях, когда возникают сомнения в достоверности различий (например, если по критерию Стьюдента различия достоверны при нулевом и недостоверны при первом уровне значимости).

Формула Фишера выглядит следующим образом:

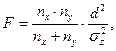(7.4)

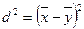где и 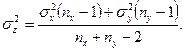(7.5, 7.6)

В рассматриваемой нами задаче d² = 5,29; σ_z² = 29,94.

Подставляем значения в формулу: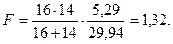

В табл. ХI Приложений находим, что для уровня значимости β₁ = 0,95 и ν = n _x + n _y – 2 = 28 критическое значение составляет 4,20.

Вывод

F = 1,32 < F_кр. = 4,20. Различия между выборками статистически недостоверны.

Примечание

При использовании критерия Фишера должны соблюдаться те же условия, что и для критерия Стьюдента (см. подраздел 7.4). Тем не менее допускается различие в численности выборок более чем в два раза.

Таким образом, при решении одной и той же задачи четырьмя различными методами с использованием двух непараметрических и двух параметрических критериев мы пришли к однозначному выводу о том, что различия между группой девушек и группой юношей по уровню реактивной тревожности недостоверны (т. е. находятся в пределах случайных вариаций). Однако могут встретиться и такие случаи, когда сделать однозначный вывод не представляется возможным: одни критерии дают достоверные, другие – недостоверные различия. В этих случаях приоритет отдается параметрическим критериям (при условии достаточности объема выборок и нормального распределения исследуемых величин).

7. 6. Критерий j* - угловое преобразование Фишера

Критерий j*Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Он оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Допускается также сравнение процентных соотношений и в пределах одной выборки.

Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол j, а меньшей доле – меньший угол, но отношения здесь нелинейные:

(7.7)

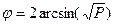
где Р – процентная доля, выраженная в долях единицы.

При увеличении расхождения между углами j₁ и j₂ и увеличении численности выборок значение критерия возрастает.

Критерий Фишера вычисляется по следующей формуле:

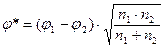(7.8)

где j₁ – угол, соответствующий большей процентной доле; j₂ – угол, соответствующий меньшей процентной доле; n ₁ и n ₂ – соответственно, объем первой и второй выборок.

Вычисленное по формуле значение сравнивается со стандартным (j*_ст = 1,64 для b₁ = 0,95 и j*_ст = 2,31 для b₂ = 0,99. Различия между двумя выборками считаются статистически достоверными, если j*> j*_стдля данного уровня значимости.

Пример

Нас интересует, различаются ли между собой две группы студентов по успешности выполнения достаточно сложной задачи. В первой группе из 20 человек с ней справилось 12 студентов, во второй – 10 человек из 25.

Решение

1. Вводим обозначения: n ₁ = 20, n ₂ = 25.

2. Вычисляем процентные доли Р ₁ и Р ₂: Р ₁ = 12 / 20 = 0,6 (60%), Р ₂ = 10 / 25 = 0,4 (40%).

3. В табл. XII Приложений находим соответствующие процентным долям значения φ: j₁ = 1,772, j₂ = 1,369.

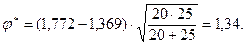Отсюда:

Вывод

Различия между группами не являются статистически достоверными, поскольку j* < j*_стдля 1-го и тем более для 2-го уровня значимости.

7.7. Использование критерия χ2 Пирсона и критерия λ Колмогорова

для оценки различий между двумя выборками

Использование критерия χ² для оценки соответствия экспериментальных распределений теоретическим (нормальному или равномерному) подробно обсуждалось в разделе 6. Тот же критерий может использоваться и для сравнения двух эмпирических распределений на предмет достоверности различий между ними.

В качестве примера рассмотрим следующую задачу:

Условие задачи

В опытах с участием 100 испытуемых (50 мужчин и 50 женщин) регистрировалось время простой сенсомоторной реакции (ВСМР) в ответ на звуковой стимул. Получены следующие результаты (табл. 7.3):

Таблица 7.3

ВСМР в секундах
Классовый Интервал	0,10 ¸ 0,12	0,12 ¸ 0,14	0,14 ¸ 0,16	0,16 ¸ 0,18	0,18 ¸0,20	0,20 ¸0,22	0,22 ¸0,24
Частоты встречаемости ВСМР
Мужчины
Женщины

Задание

Пользуясь критериемχ² Пирсона, определить, достоверны ли различия распределений ВСМР у мужчин и женщин.

Решение

1. Строим рабочую таблицу для предварительных расчетов (табл. 7.4):

Таблица 7.4

Обозна-чение интер-вала	Классовый интервал в секундах	Эмпирические частоты (мужчины)	Эмпирические частоты (женщины)	Сумма эмпирических частот	Теоретиче-ские частоты
A В C D E F G	0,10 ÷ 0,12 0,12 ÷ 0,14 0,14 ÷ 0,16 0,16 ÷ 0,18 0,18 ÷ 0,20 0,20 ÷ 0,22 0,22 ÷ 0,24				13,5 6,5 4,5 0,5
Сумма

Столбец 1 служит исключительно для экономии: в дальнейшем мы не будем указывать границы классовых интервалов – нам будет достаточно того, что распределение включает в себя 7 количественных градаций (классов). В столбцах 2, 3 и 4 отражены данные из условия задачи. Столбец 5 служит для дальнейших вычислений.

Теоретические частоты (столбец 6) в данном случае вычисляются следующим образом:

1) в случае равноценных выборок теоретическая частота в каждом классе вычисляется как среднее арифметическое двух эмпирических частот;

2) если объемы выборок различны, то теоретическая частота вычисляется как сумма эмпирических частот в данной строке, умноженная на сумму в каждом столбце (по вертикали) и отнесенная к общей сумме частот.

Для дальнейших вычислений вносим данные в табл. 7.5:

Таблица 7.5

	Мужчины	Женщины
Интервал	f эксп	.f теор.		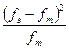f эксп	.f теор.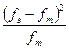
A В C D E F G		13,5 6,5 4,5 0,5	1,00 0,17 0,39 0,35 1,39 1,00 0,50		13,5 6,5 4,5 0,5	1,00 0,17 0,39 0,35 1,39 1,00 0,50

Можно видеть, что это – типичная таблица для вычисления критерия χ² (см. раздел 6). Значения в столбцах 3 и 6 для мужчин и женщин одинаковы; это естественно, так как теоретические частоты соответствуют средним значениям экспериментальных частот в каждой выборке. Тем не менее χ² следует рассчитывать, суммируя все значения в столбцах 4 и 6 (т. е. по обеим выборкам).

В итоге получаем χ² = 9,6. В табл. VI Приложений для уровня значимости 0,95 и ν = N – 1 = 6 находим значение χ²_кр., равное12,6.

Вывод

Различия между распределениями не являются статистически достоверными.

Для решения задачи можно использовать критерий Колмогорова в несколько иной модификации, нежели при сравнении экспериментального распределения с теоретическим. Для этого оформляем рабочую таблицу следующего вида (табл. 7.6):

Таблица 7.6

	Экспериментальные частоты	Накопленные экспериментальные частоты	Относительные накопленные частоты	d
Интервал	f м	f ж	F м	F ж	F *м	F *ж
A В C D E F G					0,04 0,34 0,86 0,96 1,00 1,00 1,00	0,24 0,64 0,80 0,94 0,98 1,00	0,04 0,10 0,22 0,16 0,06 0,02

Рекомендуется следующий порядок вычислений:

1. В столбце 1 – условные обозначения временных интервалов; в столбцах 2 и 3 – экспериментальные частоты мужчин (2) и женщин (3).

2. В столбцах 4 и 5 – накопленные частоты для мужчин (4) и женщин (5). Напомним, что накопленные частоты вычисляются путем простого суммирования частот от первого до последнего класса.

3. В столбцах 6 и 7 – относительные накопленные частоты (F * = F / n). Другими словами, каждая накопленная частота в столбцах 4 и 5 делится на 50.

4. Вычисляем критерий λ по формуле Колмогорова в следующей модификации:

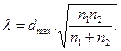(7.9)

В нашем случае:

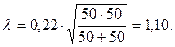
Вывод

Распределения отличаются друг от друга с вероятностью 0,822 (см. Приложения, табл. VII). Другими словами, соответствие между распределениями можно констатировать лишь с вероятностью 0,178.

Чем можно объяснить причины несоответствия результатов, полученных с помощью критериев χ² и λ? По-видимому, критерий Колмогорова, основанный на накоплении эмпирических частот, является более чувствительным к различиям и позволяет зафиксировать те тонкие нюансы, которые недоступны критерию Пирсона. Таким образом, в целом, можно усомниться в том, что различий вообще не существует. Кстати говоря, более мощные критерии (Стьюдента и Фишера), которые также можно применить к решению данной задачи, дают достоверные различия между двумя выборками на уровне значимости 0,95.

В заключение следует констатировать, что оценка различий между двумя распределениями по вышеупомянутым критериям может быть использована лишь в случае отсутствия достаточной информации о каждом конкретном значении переменной в выборках.

З а д а ч и п о т е м е

Задача 7. 1

40 студентов (20 юношей и 20 девушек) обследованы на уровень нейротизма – эмоциональной стабильности по тесту Айзенка. Полу­чены следующие результаты:

№

Юноши

Девушки

Задание

Определить достоверность различий по уровню нейротизма у юношей и девушек, выбрав один или несколько критериев, адекватных условию задачи.

Задача 7. 2

Условие задачи

В психофизиологическом эксперименте 29 юношей и 27 девушек были протестированы методике РДО (реакция на движущийся объект). В числе показателей использовался следующий критерий: величина средней ошибки S остановки движущейся точки на линии. Получены следующие значения S (в миллисекундах) для двух групп испытуемых:

Юноши	Девушки
№№	S	№№	S	№№	S	№№	S	№№	S	№№	S

Задание

Определить достоверность различий между показателями РДО для юношей и девушек, выбрав адекватный критерий обработки результатов.

З а д а ч а 7. 3

Условие задачи

Первоклассники одной из средних школ (12 мальчиков и 10 девочек) были протестированы по детскому тесту Д. Векслера на уровень интеллекта. Результаты тестирования (индивидуальные значения IQ) представлены в таблице.

Испытуемый	пол	IQ	Испытуемый	Пол	IQ
	м м м м м м м м м м м			м д д д д д д д д д д

Задание

Проанализировать полученные результаты на предмет половых различий в уровне интеллекта детей.

Задача 7.4

Условие задачи

С помощью цветового теста отношений (ЦТО) были исследованы семейные отношения у мужчин-невротиков (38 человек). Оказалось, что 74% мужчин ассоциируют свою жену с одним из светлых цветов и лишь 26% - с темным. Себя ассоциируют со светлыми цветами лишь 31% мужчин, остальные 68% - с темными.

Вопрос

Можно ли на основании приведенных выше данных утверждать, что в восприятии семьи мужчинами-невротиками наблюдается выраженная асимметрия: качества активного, доминантного, «светлого» начала больные приписывают жене, а себе оставляют пассивную, страдательную роль?

Задача 7.5

Американский исследователь Стеннет изучал связь между полом и количеством пропусков детского сада. Он получил следующие данные: более 20 дней в году пропустили 29% мальчиков и 27% девочек. Всего в его исследовании приняли участие 873 мальчика и 837 девочек.

Вопрос

Можно ли считать, что мальчики пропускают детский сад чаще девочек?

З а д а ч а 7. 6

В двух студенческих выборках (n ₁ = 27, n ₂ = 23) исследовался коэффициент интеллекта (IQ). Получены следующие результаты:

Группа1	Группа 2
№№	IQ	№№	IQ	№№	IQ	№№	IQ

Задание

Определить, достоверны ли различия распределений IQ в двух студенческих группах.

З а д а ч а 7. 7

Условие задачи

С помощью цветового теста отношений протестированы 38 человек с депрессивными симптомами и 50 человек без каких-либо выраженных психиатрических симптомов. Оказалось, что свое настроение ассоциируют с яркими цветами (красный, желтый, зеленый) 40% здоровых и 5% депрессивных испытуемых. Свое прошлое ассоциируют с аналогичными цветами 14% больных против 22% здоровых.

Задание

Определить достоверность различий между данными группами испытуемых.

________________________________________________________________________________

РАЗДЕЛ 8

МЕРЫ СВЯЗИ

8. 1. Постановка проблемы

Многие психологические черты, свойства, признаки не являются независимыми, а определенным образом взаимосвязаны между собой. Поэтому психологу часто приходится иметь дело с выявлением наличия и характера связи между этими признаками, свойствами, чертами. Это позволяет в известной степени минимизировать число изучаемых признаков, объединяя их в более крупные конгломераты, особенно в тех случаях, когда число таких признаков достаточно велико.

В математическом смысле задача состоит в нахождении связи между двумя рядами переменных (x _i и y _i), измеренных на одной и той же выборке испытуемых. О наличии связи (корреляции) между этими переменными можно говорить в тех случаях, когда изменение величины х ведет к закономерному изменению величины у,и если характер изменений является предсказуемым.

8. 2. Представление данных

Данные о связи двух переменных могут быть представлены либо графически (в виде диаграмм рассеивания), либо путем вычисления коэффициентов корреляции по соответствующим формулам.

В графическом изображении каждый испытуемый может быть представлен точкой в координатах у = f (х), причем величины х _i и у _iсоответствуют значениям двух исследуемых признаков. Выборка испытуемых в этих координатах представляет собой «облако рассеивания» точек, которое может иметь различную форму (рис. 8.1).

 

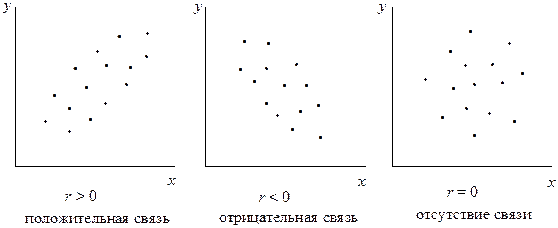
Рис. 8.1. Графическое представление связи между переменными (облако рассеивания точек имеет различную форму в зависимости от характера связи), объяснение в тексте

При наличии прямой (положительной) связи между переменными облако рассеивания имеет более или менее уплощенную эллиптическую форму, длинная ось которого направлена вправо и вверх. Другими словами, при возрастании значения одной переменной имеется тенденция к увеличению другой переменной.

В случае отрицательной связи между переменными длинная ось облака рассеивания направлена вправо вниз, т. е., увеличение значений одной переменной соответствует закономерному снижению значений другой.

Наконец, если облако рассеивания имеет округлую форму, то можно предположить, что корреляция между переменными отсутствует или, по крайней мере, она весьма незначительна.

В психологии используется несколько различных мер связи (коэффициентов корреляции), выбор которых определяется в первую очередь типом шкалы, который формирует исследуемая переменная величина. Чаще всего коэффициенты корреляции представляют собой величины, стандартизованные таким образом, что они могут принимать значения от –1 (строгая обратная связь) до +1 (строгая прямая связь). Вычисление коэффициента корреляции предполагает также определение его статистической значимости (достоверности) по соответствующим формулам или таблицам. Достоверность коэффициента корреляции может быть определена для определенного уровня значимости (0,95, 0,99 и т. д.).

8. 3. Коэффициент корреляции Фехнера

Коэффициент корреляции, предложенный во II–й половине XIX века Г. Т. Фехнером, является наиболее простой мерой связи между двумя переменными. Он основан на сопоставлении двух психологических признаков x_i и y_i, измеренных на одной и той же выборке, по сопоставлению знаков отклонений индивидуальных значений от среднего: 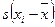и 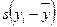. Вывод о корреляции между двумя переменными делается на основании подсчета числа совпадений и несовпадений этих знаков.

Дата добавления: 2014-11-29