Подготовка данных к математической обработке

Прежде чем приступать к математической обработке результатов психологического исследования, экспериментальный материал необходимо соответствующим образом подготовить. При этом психологу следует соблюдать два непременных условия. Во-первых, данные должны быть представлены в наиболее компактной, удобной для обработки форме. Во-вторых, при упорядочении данных должен быть сохранен максимум содержащейся в них информации.

Подготовка данных к математической обработке включает в себя ряд последовательных этапов: протоколирование, табулирование данных, создание таблиц сгруппированных частот, построение диаграмм или полигона распределения частот и т. д. Рассмотрим все этапы более подробно.

3. 1. Протоколирование данных

Если психолог имеет под рукой персональный компьютер, задача протоколирования значительно упрощается. Любой программист может составить соответствующую базу данных, и все необходимые сведения о каждом испытуемом можно заносить в компьютер. Несомненное удобство компьютерного варианта состоит в том, что в любой момент можно извлекать информацию об интересующем нас контингенте испытуемых – по полу, возрасту, социальной принадлежности и др. При отсутствии такой возможности на каждого испытуемого составляется отдельный протокол.

В протоколе необходимо отмечать фамилию и инициалы испытуемого, пол и возраст (за исключением случаев анонимного обследования, когда указываются только инициалы, пол и возраст). Несоблюдение этих требований делает невозможным дальнейший анализ результатов (в тех случаях, когда нас интересует связь исследуемой переменной с возрастом и полом испытуемых).

Весьма желательно указывать в протоколе дату исследования. Это особенно важно в тех случаях, когда исследование одной и той же выборки проводится повторно (период времени между повторными исследованиями, например, две недели или полгода) имеет большое значение, особенно когда речь идет о детях.

В некоторых случаях необходимо указывать время суток, когда проводилось исследование. Так, некоторые психологические и психофизиологические переменные (время сенсомоторной реакции, концентрация и переключаемость внимания, объем оперативной памяти и др.) в значительной мере зависят от уровня активности субъекта, степени его утомления, которые далеко не одинаковы в разное время суток.

При необходимости в протоколе следует отмечать условия опыта (проводилось ли исследование индивидуально или в группе, наличие внешних помех и т. д.). Все другие данные о каждом или отдельных испытуемых исследователь отмечает по своему усмотрению, т. е. фиксируется то, что психолог считает наиболее важным.

3. 2. Составление сводных таблиц (табулирование данных)

Использование индивидуальных протоколов для математической обработки результатов не очень удобно. Для того, чтобы представить материал в более компактном виде, данные сводятся в итоговую таблицу следующего вида:

№№ п/п.	Фамилия, имя, отчество	Другие данные (если необходимо)	Исследуемый показатель
…
n

В ряде случаев перед составлением сводной таблицы проводится ранжирование данных. Оно, в частности, необходимо при определении квантилей (см. подраздел 3.3). Для этого данные выстраиваются в общий ряд по исследуемому признаку в порядке его возрастания (или убывания) следующим образом: х ₁≤ х ₂≤ х ₃≤ ... ≤ х _n (или наоборот), где n – общее число значений признака (объем выборки). Знак «меньше или равно» предполагает, что у разных испытуемых могут встречаться одинаковые значения переменной.

Иногда даже итоговые таблицы могут оказаться довольно громоздкими и не вполне удобными для дальнейшей обработки. В этом случае материал можно сделать еще более компактным, составляя частотные таблицы (таблицы распределения частот исследуемого признака):

№№ пп.					...	n – 1	n
x i
f i

В первой строке дается номер значения переменной в ранжированном ряду, во второй – конкретное значение (величина признака) и в третьей – частота встречаемости признака (число одинаковых значений признака в выборке).

Для того чтобы полученные данные представить в еще более компактном виде, используются таблицы распределения сгруппированных частот. Для составления такой таблицы необходимо:

1) общий диапазон изменения признака разделить на ряд поддиапазонов (классов) при условии, что ширина всех классов должна быть одинакова;

2) определить границы классов и их число в общем диапазоне;

3) подсчитать частоты встречаемости признака в каждом классе.

Обычно для построения распределения сгруппированных частот используется 7 – 15 классов. Для наиболее точного разбиения диапазона на классы (если в дальнейшем предполагаются математические операции с этими классами) можно использовать формулу Стэрджесса: N = 1 + 3,322 lg n, где n – объем выборки (количество значений признака), а N – количество классов. Так, например, если n = 100, то N = 1 + 3,322 × 2» 8.

Пример

На выборке испытуемых численностью 100 человек определялся коэффициент интеллекта (IQ). Минимальное значениеIQоказалось равным 72, а максимальное – 134. Для составления таблицы сгруппированных частот используем 8 классов (в соответствии с формулой Стэрджесса). Определяем общий диапазон изменения признака – он будет соответствовать разнице между минимальным и максимальным значениями: 134 – 72 = 62. Следовательно, в каждый класс должно попадать по 8 значений признака (при разбиении на классы можно слегка расширить диапазон с тем расчетом, чтобы в каждом классе оказалось одинаковое число значений и чтобы крайние значения не оказались за пределами диапазона). В соответствии с этим определяем границы классов и составляем таблицу сгруппированных частот:

Номер класса (N)				...
Границы класса (x min ¸ x max)	72 ¸ 79	80 ¸ 87	88 ¸ 95	...	128 ¸ 135
Среднее значение (х¯)	75,5	83,5	91,5	...	131,5
Частоты (f i )				...
Накопленные частоты (F i)				…

Накопленные частоты, приведенные в 5-й строке, могут быть использованы в некоторых статистических расчетах (например, для вычисления критерия l по Колмогорову). Накопленные частоты вычисляются путем простого суммирования частот от 1-го до N -го класса: F ₁ = f ₁; F ₂ = f ₁ + f ₂; F ₃ = f ₁ + f ₂ + f ₃ и т. д.

3. 3. Определение квантилей

Квантиль – точка на числовой оси (значение признака), делящая совокупность наблюдений в определенной пропорции. Определение квантилей достаточно часто используется в психодиагностических процедурах (при определении тестовых норм и т. д.). Для определения квантилей необходимо иметь ряд значений исследуемого признака, ранжированных в порядке возрастания величины.

Различают несколько разновидностей квантилей:

а) квартили (Q)делят совокупность наблюдений (ранжированный ряд) на 4 равные части: 1-й квартиль (Q ₁) делит ряд в соотношении 25:75%, 2-й (Q ₂) – в соотношении 50:50% и 3-й (Q ₃ ) – в соотношении 75:25%.

б) квинтили (K) делят выборку на 5 равных частей: K ₁ – в соотношении 20:80%, K ₂ – 40: 60%, K ₃ – 60:40%, K ₄ – 80:20%.

в) децили (D) делят ранжированный ряд на 10 равных частей: D ₁ = 10%, D ₂ = 20%,... D ₉ = 90%.

г) наконец, процентили (Р) делят совокупность наблюдений на 100 частей (в процентном отношении).

Соотношения квантилей можно представить в виде следующей схемы:

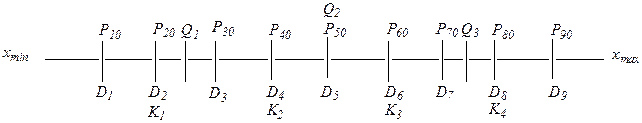
Пример

На 20 испытуемых определялся уровень личностной тревожности (УЛТ) по тесту Спилбергера. При ранжировании значений признака получен следующий вариационный ряд (см. таблицу). Задача состоит в том, чтобы определить значения 1-го, 2-го и 3-го квартилей.

№№

УЛТ

Q ₁ = 36 Q ₂ = 41,5 Q ₃ = 45

Для определения значений квартилей разбиваем ранжированный ряд на 4 равные части (по 5 значений признака). 1-й квартиль располагается между 5-м и 6-м значениями ряда, оба из которых соответствуют 36. Следовательно, Q ₁ = 36. 2-й квартиль расположен между 10-м значением, равным 41, и 11-м, равным 42. Представляется разумным определить значение 2-го квартиля как среднее между двумя смежными значениями (Q ₂ = 41,5). Значение 3-го квартиля лежит между 15-м и 16-м значениями ряда (Q ₃ = 45).

Точно так же мы можем определить значения квинтилей (разбиение ранжированного ряда на 5 частей по 4 значения признака) или децилей (разбиение ряда на 10 равных частей по 2 значения переменной в каждой).

3. 4. Графическое представление результатов

Графическое представление результатов психологического исследования имеет ряд несомненных преимуществ перед табличным (цифровым) материалом в тех случаях, когда речь идет о докладах, научных отчетах и сообщениях, диссертационных работах и т. д. Графическое представление наиболее наглядно, оно позволяет визуально представить полученные закономерности, связи и пр. В данном разделе мы коснемся лишь графического представления распределений исследуемого признака.

В основе графического представления лежат составленные заранее таблицы сгруппированных частот. Первый вид представления – построение столбчатых диаграмм (иначе, гистограмм) распределения признака (рис. 3.1, а). Гистограммы строятся в координатах f = j (x _i), где по оси абсцисс откладываются значения признака (x _i), а по оси ординат – частота встречаемости признака (f). Ширина каждого столбца гистограммы соответствует ширине класса, а высота столбца – частоте встречаемости признака в данном классе.

Вместо диаграмм можно использовать построение полигона распределения (рис. 3.1, б). В этом случае распределение отображается в виде точек, соединенных друг с другом прямыми линиями. Координаты каждой точки соответствуют среднему значению класса (по оси абсцисс) и частоте встречаемости признака в данном классе (по оси ординат).

f _i

x _i

а б

Рис. 3.1. Графическое представление результатов исследования: а – столбчатая диаграмма (гистограмма) распределения (зачерненный столбец соответствует модальному классу); б) полигон распределения. По оси абсцисс – значение исследуемого признака (x _i), по оси ординат – частота встречаемости данного значения признака (f)

раздел 4

МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ

Центральная тенденция – то количественное (численное) значение признака, к которому тяготеет переменная величина. Поскольку понятие «тяготеет» несколько произвольно и с математической точки зрения не вполне корректно, имеет смысл рассмотреть различные меры центральной тенденции более подробно.

В психологических исследованиях в качестве мер центральной тенденции чаще всего используются мода, медиана и среднее арифметическое значение. Значительно реже используются такие меры как среднее геометрическое, среднее гармоническое, обратное среднее гармоническое значение и др.

4. 1. Мода

Мода (Mo) – наиболее часто встречающееся значение признака. В предыдущем примере (ранжированный ряд уровня личностной тревожности) мы имеем две моды: Mo ₁ = 36 и Mo ₂ = 45 (эти значения переменной встречаются трижды, в то время как все остальные – по 1 или 2 раза). В зависимости от того, сколько значений признака удовлетворяют определению моды, различают мономодальные (имеющие одну моду), бимодальные (имеющие две моды) и полимодальные распределения(имеют более чем две моды), а также распределения, не имеющие моды (все значения признака встречаются примерно с одинаковой частотой). В бимодальном и полимодальном распределениях, в свою очередь, можно определить наибольшую и наименьшую моды.

В тех случаях, когда анализируются таблицы сгруппированных частот исследуемого признака, как правило, определяется модальный класс, т. е. тот класс распределения, в который попадает наибольшее количество частот (значений признака). Так, для иллюстрации зачерненный столбец на рис. 3.1, а соответствует модальному классу.

Мода не является достаточно строгой мерой центральной тенденции, поскольку она не учитывает характера распределения переменных, а значит может использоваться лишь в предварительных выводах и прогнозах. Кроме того, необходимо использовать моду только для больших объемов выборок, поскольку для малых она недостаточно информативна.

4. 2. Медиана

Медиана (Md) – значение, которое делит упорядоченное множество данных (ранжированный ряд) пополам так, что одна половина значений оказывается больше, а другая – меньше медианы. Медиана – среднее значение ранжированного ряда. Если число значений нечетное, то медиана соответствует среднему члену ряда, если четное, то медиана есть среднее между двумя центральными значениями (в предыдущем примере Md = 41,5).

Медиана соответствует 50-му процентилю, 5-му децилю или 2-му квартилю в группе данных, т. е. Md = P ₅₀ = D ₅ = Q ₂.

Мода и медиана не учитывают разброса данных, и переменные, лежащие в стороне от центра, не влияют на их величину.

4. 3. Среднее арифметическое значение

Среднее арифметическое значение,или просто среднее (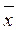), равно сумме переменных, деленной на их число.

Для несгруппированных переменных среднее арифметическое вычисляется по формуле:

(4.1)

Для сгруппированных переменных можно воспользоваться другой формулой – среднее будет соответствовать сумме произведений средних значений каждого класса и частоты встречаемости значения признака в данном классе:

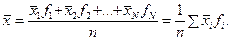(4.2)

Среднее арифметическое может использоваться и для тех признаков, для которых не найден способ количественного измерения (шкала порядка). Для этого в качестве x _i используются ранговые числа, а среднее принято называть непараметрическим средним.

Взвешенное среднее арифметическое используется в тех случаях, когда разные составляющие имеют разный «удельный вес» в формировании общей совокупности:

(4.3)

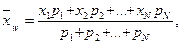или: (4.4)

где n – объем выборки, N – число классов.

Пример

Средний балл аттестата учащихся выпускных классов одной из школ соответствует следующим значениям: 11-а – 4,2; 11-б – 4,0 и 11-в – 3,8. Численность этих классов составляет: 11-а – 25 человек, 11-б – 28 и 11-в – 32 человека. В данном случае средний балл аттестата по всем выпускным классам составит (4,2 × 25 + 4,0 × 28 + 3,8 × 32): (25 + 28 + 32) = 3,98.

Среднее принято округлять с точностью до знака, следующего за последним знаком x_i (увеличение точности на порядок).

Свойства среднего

1. Сумма всех отклонений от среднего значения равна нулю:

Доказательство:

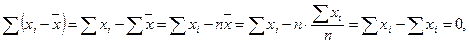поскольку `

2. Если константу с прибавить к каждому значению, то среднее превратится в

Доказательство:

3. Если каждое значение множества со средним умножить на константу c, то среднее станет равным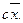

Доказательство:

4. Сумма квадратов отклонений значений от их среднего арифметического меньше суммы квадратов отклонений от любой другой точки: (приусловии, что b ¹`x).

Доказательство: 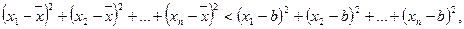где

Примем Тогда:

поскольку

Так как c ² > 0, то:

4. 4. Среднее геометрическое значение

Среднее геометрическое значение (x_g) используется для вычисления центральной тенденции при прогрессивно возрастающих квантилях (когда распределение значений переменной имеет выраженную положительную (правостороннюю) асимметрию).

Формула среднего геометрического:

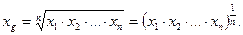(4.5)

Для вычислений можно использовать логарифмирование каждой переменной по основанию е:

(4.6)

Переход от ln x_g к x_g осуществляется с помощью операции антилогарифмирования:

(4.7)

З а д а ч и п о т е м е

Задача 4.1

Условие задачи

У 50 школьников выпускных классов исследовался коэффициент интеллекта (IQ). Получен следующий вариационный ряд (см. табл.).

№№

IQ

№№

IQ

№№

IQ

№№

IQ

№№

IQ

Задание

1. Построить ранжированный ряд IQ.

2. Построить таблицу сгруппированных частот для 7 ¸ 8-классового распределения.

3. Построить графическое выражение IQ в виде полигона распределения или столбчатой диаграммы.

4. Определить 1-й, 2-й и 3-й квартили, моду, медиану и среднее арифметическое значение коэффициента интеллектуальности для выборки в 50 испытуемых.

Задача 4.2

Условие задачи

В трех выпускных классах средней школы подсчитывался средний балл успеваемости. Получены следующие результаты:

	11-а класс	11-б класс	11-в класс
Пол	Число учащихся	Балл	Число учащихся	Балл	Число учащихся	Балл
Девочки		3,62		3,90		3,75
Мальчики		3,44		3,58		3,70

Задание

Вычислить средний балл успеваемости у девочек и мальчиков всех выпускных классов.

Задача 4. 3

Имеется следующая совокупность экспериментальных данных: 1,00; 1,26; 1,58; 2,00; 2,51; 3,16; 3,98; 5,01; 6,31; 7,94.

Задание

Вычислить среднее геометрическое значение данной совокупности двумя способами:

а) вычислением произведения значений и возведения в соответствующую степень;

б) путем логарифмирования по основанию e.

________________________________________________________________________________

РАЗДЕЛ 5

МЕРЫ ИЗМЕНЧИВОСТИ (РАЗНООБРАЗИЯ, ВАРИАТИВНОСТИ) исследуемого ПРИЗНАКА

Две выборочные совокупности могут иметь одинаковые или близкие между собой средние значения признака и в то же время существенно различаться по степени вариабельности (вариативности) этого признака.

Например, имеется две группы испытуемых (по 100 человек в каждой), у которых исследуется коэффициент интеллекта (IQ). Средние значения IQ в той и другой группе могут приблизительно совпадать (допустим, IQ₁ = 102 и IQ₂ = 97), и констатация этого факта даст нам очень немного информации. В то же время известно, что индивидуальные значения в первой группе испытуемых изменяются от 85 до 116, а во второй от 60 до 135. На основании этого мы можем сказать, что вторая выборка обладает большим разнообразием признака по сравнению с первой.

Для определения степени разнообразия (изменчивости) исследуемого параметра используются различные критерии: пределы разнообразия, размах вариаций, среднее и стандартное отклонения, дисперсия, коэффициент вариации и др.

Дата добавления: 2014-11-29