Лимиты (пределы) разнообразия

Лимит (предел) разнообразия - это указание наименьшей и наибольшей величины признака среди всех представителей группы:

(5.1)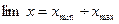

Другими словами, предел разнообразия признака не вычисляется, а лишь констатируется. Так, в приведенном выше примере lim x ₁ = 85 ¸ 116 и lim x ₂ = 60 ¸ 135.

5. 2. Размах вариаций

Размах вариаций (r)есть математическая разность между максимальной и минимальной величиной признака:

(5.2)

В нашем примере размах вариаций в первой группе (r₁)составляет 116 – 85 = 31 и во второй (r₂) –135 – 60 = 75.

Размах от 10-го до 90-го процентиля (мера D)вычисляется следующим образом:

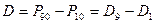(5.3)

Другими словами, для вычисления меры D отсекается по 10% значений с левого и правого края распределения и определяется размах вариаций для оставшихся 80%. Эта мера более стабильна, чем включающий и исключающий размах, поскольку на него не влияют крайние (возможно, случайные) значения вариаций.

Междуквартильный размах – еще более жесткая мера изменчивости, нежели мера D. Междуквартильный размах – это разность между 1-м и 3-м квартилями группы:

(5.4)

Другими словами, для определения междуквартильного размаха с краев распределения признака отсекается по 25% значений и определяются границы для оставшихся (наиболее типичных) 50%, которые в максимальной степени характеризуют центральную тенденцию.

Полумеждуквартильный размах (Q _1/2) равен половине расстояния между 1-м и 3-м квартилями:

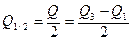(5.5)

Суть этой статистической меры состоит в уравнивании между собой расстояний между 1-м и 2-м и между 2-м и 3-м квартилями, которые в случае несимметричных распределений могут отличаться друг от друга. В случае же симметричного распределения полумеждуквартильный размах включает в себя приблизительно 25% данных.

5. 3. Среднее отклонение

Среднее отклонение (MD) – параметрическая мера изменчивости, предложенная в свое время Г. Т. Фехнером. Среднее отклонение равно сумме отклонений от среднего значения (или, другими словами, сумме расстояний между x _i и 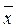), взятых по модулю:

(5.6)

5. 4. Дисперсия

Дисперсия (s²)представляет собойсумму квадратов отклонений от среднего (сумму квадратов расстояний между x _i и ):

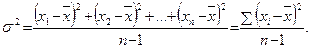(5.7)

Деление суммы квадратов на число степеней свободы n – 1 позволяет сравнивать между собой совокупности, различные по объему. Считается, что дисперсия – более мощный статистический критерий, нежели среднее отклонение, так как больший вклад в дисперсию дают те значения признака, которые расположены дальше от среднего (вклад каждого значения в дисперсию возрастает пропорционально квадрату отклонения от среднего).

Формула 5.7 не очень удобна при расчете дисперсии вручную (на микрокалькуляторе). Поэтому для этих целей можно использовать другую (рабочую) формулу, которую можно получить путем соответствующих преобразований.

Преобразование формулы:

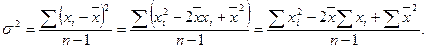
Но . Отсюда следует, что:

Так как , то:

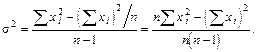(5.8)

Свойства дисперсии:

1. Дисперсия не изменится, если к каждому значению x_i прибавить константу c: x _j = x _i + c Þ s_j² = s_i².

2. Умножение на константу c каждого значения x_i увеличивает дисперсию в c ² раз: x_j = сx_i Þ s_j² = с ² × s_i².

5. 5. Среднеквадратичное (стандартное) отклонение

Стандартное отклонение (s_х) соответствует квадратному корню из дисперсии. Наряду с дисперсией является одной из наиболее часто используемых мер вариабельности признака.

(5.9)

5. 6. Коэффициент вариации

Коэффициент вариации (V) есть отношение стандартного отклонения к среднему арифметическому значению, выраженное в процентах:

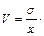100 % (5.10)

З а д а ч и п о т е м е

Задача 5. 1

В психофизиологическом эксперименте регистрировалось время простой сенсомоторной реакции у 50 испытуемых в ответ на звуковой стимул средней интенсивности. Получены следующие значения времени реакции (ВР) в миллисекундах:

№	Т, мс	№	Т, мс	№	Т, мс	№	Т, мс	№	Т, мс

Задание

1. Определить размах вариаций, междуквартильный и полумеждуквартильный размах, среднее отклонение, дисперсию, стандартное отклонение и коэффициент вариации.

2. Построить обычную и кумулятивную кривые распределения ВР. Определить процентное соотношение частот при нормировании распределения по стандартному отклонению от – 4 до + 4s с шагом в 1s.

3. Определить размах распределения признака в единицах стандартного отклонения.

З а д а ч а 5. 2

Условие задачи

Проведено тестирование двух групп испытуемых (по 10 человек в каждой) на уровень личностной тревожности (УЛТ) по Спилбергеру. Получены следующие результаты:

№
УЛТ1
УЛТ2

Задание

Определить средние значения УЛТ, стандартные отклонения и коэффициенты вариаций для каждой группы испытуемых, сравнить их между собой, сделать выводы.

РАЗДЕЛ 6

РАСПРЕДЕЛЕНИЯ ПЕРЕМЕННЫХ ВЕЛИЧИН

В разделах 3 и 4 были даны основные представления о распределениях переменных величин (моно-, би-, полимодальные и др.). В этих случаях речь шла о характере эмпирических (экспериментальных) распределениях, которые могут иметь весьма разнообразный (зачастую непредсказуемый) характер. Подойдем к данному вопросу с несколько иной стороны. Кроме эмпирических (построенных на основе данных экспериментального исследования) существуют и теоретические распределения. Любое теоретическое распределение представляет собой определенную математическую модель, которой (с определенной долей вероятности) могут соответствовать (или не соответствовать) экспериментальные распределения. Перед психологом достаточно часто возникает проблема сопоставления экспериментального распределения с теоретическим – в плане выбора наиболее адекватного метода математической обработки результатов (см. раздел 7), для прогнозирования вероятности тех или иных событий и т. д. В данной главе будут рассмотрены лишь те виды распределений, с которыми психологам приходится встречаться особенно часто. Особое внимание будет уделено нормальному распределению. Кроме него, будут рассмотрены равномерное, биномиальное распределение и распределение Пуассона.

6.1. Нормальное распределение

6. 1. 1. Основные понятия

Нормальное распределение (распределение Гаусса, распределение Муавра – Лапласа) – это распределениезначенийпеременной величины в тех случаях, когда она варьирует случайным образом и не подвержена влиянию какого-либо систематического фактора.

Формула нормального распределения:

(6.1 а, б)

где: f – теоретическая частота встречаемости значения x_i; s – стандартное отклонение; a, b – константы; p» 3,142 (отношение длины окружности к диаметру); e» 2,718 (основание натурального логарифма).

Теоретическое нормальное распределение имеет вид симметричной колоколообразной кривой, которая подчиняется следующим закономерностям:

1. Правая и левая ветви теоретического нормального распределения абсолютно симметричны и как бы зеркально отражают друг друга.

2. В нормальном распределении основные показатели центральной тенденции (мода, медиана и среднее арифметическое значение) совпадают и соответствуют самой высокой точке (вершине) распределения.

3. Правая и левая ветви распределения уходят в бесконечность, никогда не соприкасаясь с осью абсцисс. Другими словами, частота (вероятность) встречаемости того или иного значения признака может быть сколь угодно мала, но никогда не равна нулю. В практическом отношении это свойство нормального распределения весьма неудобно, так как погоня за бесконечностью – занятие весьма неблагодарное. Поэтому принято анализировать полученные данные в диапазоне от –4 до +4 стандартных отклонений (теоретически в этот диапазон должно попадать ~ 99,98% экспериментальной выборки). В то же время сужение диапазона до ±3 σ несколько рискованно, так как значения, даваемые «крайними» испытуемыми, могут выпасть из рассмотрения.

При переводе экспериментальных значений в единицы стандартного отклонения может быть использована мера Пирсона z = (x _i - )/s_х. На рис. 6.1 показаны теоретические частоты встречаемости значений признака (в процентном соотношении) при разбиении диапазона от –4 до +4 s на восемь равных классов (ширина каждого класса соответствует одному стандартному отклонению), а также соответствующие 8-классовому распределению кумулятивные (накопленные) частоты (рис. 6.2). Эти численные значения могут понадобиться для сравнения экспериментально полученного распределения с теоретическим.

Рис. 6.1. Кривая нормального распределения

»0,1%»2,3%»15,9%»50%»84,1%»97,7%»99,9%»100%

Рис. 6.2. Кумулятивная кривая нормального распределения

Кроме 8-классового, иногда используют 16-классовое распределение – в этом случае диапазон от –4 до +4 s разбивают на 16 равных классов с шагом 0,5 стандартных отклонения.

Зная распределение частот в нормальном распределении, можно решить обратную задачу – определить размах (в единицах стандартного отклонения), в который укладывается определенное количество (процент) значений выборочной совокупности. Так, 90% выборки укладываются в пределах ±1,645s; 95% соответствуют ±1,96s; 99% соответствуют ±2,58s;99,9% укладываются в ±3,29s. Как будет показано далее, эти соотношения имеют большое значение для определения достоверности некоторых статистических выводов при разных уровнях значимости.

Двумерное нормальное распределение можно получить, измеряя две относительно независимые друг от друга переменные. Оно строится в трехмерном пространстве, в координатах f (x, y) и имеет колоколообразный вид.

Как отмечалось ранее, распределения переменных величин, получаемые в эксперименте, имеют определенную степень приближения к теоретическому (нормальному) распределению. В данном случае степень соответствия эмпирического распределения нормальному позволяет определить, насколько случайно или закономерно варьирует тот или иной показатель, подвержен ли он влиянию каких-либо систематических факторов и т. д.

Существует ряд статистических критериев, позволяющих сравнить экспериментально полученное распределение с теоретическим (нормальным). Основными из них являются коэффициент асимметрии, показатель эксцесса, критерий хи-квадрат Пирсона (c ²) и критерий lКолмогорова - Смирнова.

6. 1. 2. Коэффициент асимметрии

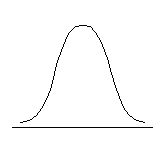
Распределение может быть приблизительно симметричным относительно моды либо обладать отрицательной или положительной асимметрией. Положительно асимметричным считается распределение с более крутым левым и более пологим правым крылом, распределение с отрицательной асимметрией, напротив, имеет более пологий левый фронт нарастания и более крутой правый (см. рис. 6.3.).

Отрицательная асимметрия, As < 0	Симметричное распределение, As = 0	Положительная асимметрия, As > 0

Рис. 6.3. Типы асимметрии

Рассчитываемый по соответствующим формулам коэффициент асимметрии (As) может быть использован в качестве одного из критериев соответствия экспериментального распределения теоретическому.

Вычисление коэффициента асимметрии:

Коэффициент асимметрии вычисляется по следующей формуле:

(6.2)

где z _x – мера Пирсона .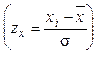

При больших выборках (n > 50) можно использовать упрощенную формулу:

(6.3)

Соответствие эмпирического распределения нормальному находится по соответствующим таблицам (в нашем приложении – табл. I). При этом эмпирическое распределение считается соответствующим теоретическому (нормальному), если асимметрия при данной выборке не превышает граничного значения.

Пример

Распределение значений исследуемого признака для выборки в 100 человек обнаружило коэффициент асимметрии As = 0,55.

Вопрос: соответствует ли данное распределение нормальному?

Решение: в табл. I находим, что для n = 100 As _кр. = 0,39 (для b₁ = 0,95) и As _кр. = 0,57 (для b₁ = 0,95).

Ответ: распределение статистически достоверно отличается от нормального с вероятностью 0,95, поскольку As _эксп.> As _кр. С вероятностью же 0,99 аналогичного вывода мы сделать не можем(As _эксп. < As _кр.).

Причины асимметрии могут быть различными. Во-первых, это возможное действие побочных однонаправленных факторов. Так, например, в тестах на измерение интеллекта могут преобладать сложные задания, с которыми большинство испытуемых не справляется. Это может явиться причиной положительной асимметрии (центральная тенденция лежит слева от среднего значения). Во-вторых, это ограничение (сверху или снизу) размаха вариаций. Например, при измерении времени сенсомоторной реакции нижний предел реагирования лимитирован физиологическими возможностями субъекта, в то время как верхний жестко не ограничен. Наконец, третьей причиной асимметрии может быть неоднородность выборки (например, если исследование проводится в смешанной группе разного возраста). При этом имеет место наложение друг на друга двух или нескольких разных по численности и сдвинутых относительно друг друга по моде распределений.

Дата добавления: 2014-11-29